小６算数「比と比の利用」指導アイデア《比が等しいことの意味の理解》

特集: 1人1台端末時代の｢教科指導のヒントとアイデア｣

2023.10.19

単元の展開

第１時　ご飯の材料の分量の割合について考える。
▼
第２時　ご飯の材料の分量の割合について考え、比を用いた割合の表し方、比の値を知る。
▼
第３時（本時）棒と影の長さの比の値を調べ、２つの比が等しいことの意味を理解する。
▼
第４時　等しい比が複数あることを見付け、２つの比の間に成り立つ性質について考える。
▼
第５時　等しい比の性質を使い、同じ濃さの乳酸飲料の量を考える。
▼
第６時　等しい比の性質を使って、できるだけ小さい整数の比を見付ける。
▼
第７時　等しい比の性質を利用して、影の長さを基に木の高さを求める。
▼
第８時　72㎝のリボンを使い、比例配分の意味と計算の仕方を考える。
▼
第９時　黄金比・白銀比を知り、身の回りのものの比について考える。

本時のねらい

棒と影の長さの関係に着目し、それらの割合を比べる活動を通して、比の相等やその判断の方法を考える。

評価規準

比の値を用いて、２つの比が等しいかどうかを判断することができる。（知識及び技能）

本時の展開

導入の最初の問題では、｢80㎝の棒の長さに対して影の長さが40㎝」という「半分」に着目させるような数値の工夫を取り入れ、同じ時刻では棒の長さと影の長さの比が等しいことを押さえます。次に、別の時刻の場合を示し、影の長さと棒の長さの割合を考えることを通して、比の相等と比の値の関係という本時の主眼へとつなげていきます。

●影の長さが棒の長さの半分の場面を提示

お昼に80㎝の棒をまっすぐに立てて、影の長さを測ったら40㎝でした。

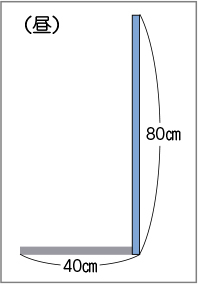
（100㎝の棒の図を提示する）実は100㎝の棒も別に立てていました。影の長さは何㎝になると思いますか。

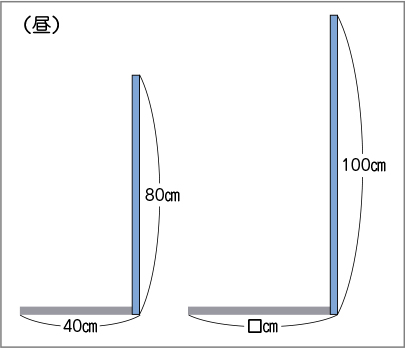
50㎝になると思います。

なぜですか。

80㎝の棒の半分の長さが影の長さになっているから、100㎝の半分の50㎝だと思いました。

どちらも影の長さが棒の長さの半分になると考えたのですね。その通りで50㎝になりました。次に、影の長さと棒の長さの関係を割合で考えてみましょう。80㎝の棒の長さを基にすると、40㎝の影の長さの割合はいくつになっていますか。

0.5です。

どのようにして分かりましたか。

棒の長さが基にする量で、影の長さが比べる量です。だから、40÷80を計算して0.5になります。

※数直線図も適宜示す。

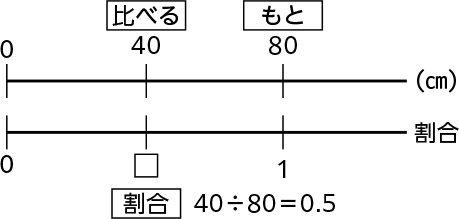
棒の長さと影の長さの関係を倍という言葉を使って言えますか。

影の長さは棒の長さの0.5倍です。

0.5は[MATH]\(\frac{1}{2}\)[/MATH]に等しいから、影の長さは棒の長さの[MATH]\(\frac{1}{2}\)[/MATH]倍と言ってもよいです。

さっき言っていた半分は、[MATH]\(\frac{1}{2}\)[/MATH]倍とも言えるということですね｡（棒が100㎝の場合も同様に確認する）ところで、今、比の勉強をしていますね。影の長さと棒の長さを比で表してみましょう。影の長さが40㎝、棒の長さが80㎝のときは、比はどうなりますか。

40：80です。

では、棒の長さが100㎝のときは、何対何ですか。

50：100です。

そうですね。同じ時刻に棒を立てたとき、棒の長さが80㎝でも100㎝でも、棒の長さを基にしたときの影の長さの割合はどちらも0.5または[MATH]\(\frac{1}{2}\)[/MATH]だから、40：80と50：100は等しい比と言えますね｡（前の授業までで学習した、表現は異なるが同じ割合を表す比［２：３と４：６など］を想起させる）

※比の順序は、一貫して「影：棒」とし、棒の長さを基にする量、影の長さを比べる量とする。

●影の長さが棒の長さの半分でない場面の提示

実は、夕方の17時にも棒を立てて、影の長さを測ってみました。すると、48㎝の棒の影の長さは84㎝になっていました。

わー、今度は棒の長さより影の長さのほうが長くなったんだね。

影の長さと棒の長さの比は何対何ですか。

84：48です。

そうですね。40㎝の棒も立ててみました｡（①、②、③の棒と影の図を提示し、それらの比を子供と確認する）次の①、②、③のうち、同じ時刻の17時に40㎝の棒を立てたときの図はどれでしょうか。

夕方17時に48㎝のぼうをまっすぐに立てたら、かげの長さは84㎝でした。次の①、②、③のうち、17時のときのぼうとかげを表しているのはどれでしょう。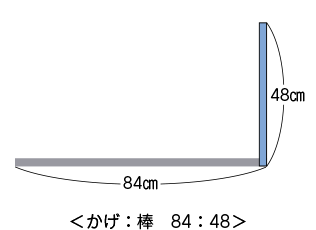

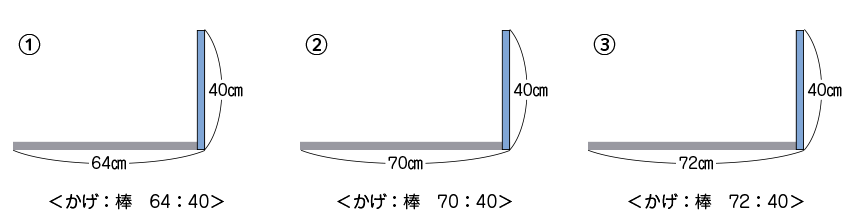
どのように調べたらよいでしょうか。

さっきやったように、割合や倍を調べるとよいと思います。

前の時間に比の値を学習したので、比の値を調べてみようと思います。

それでは、まずは各自で調べていきましょう。

１人１台端末活用アイデア

棒と影の問題場面を、ロイロノートなどのアプリからカードを児童用タブレットに配信することで、紙のワークシートやカードを作って配る手間を省くことができます。また、それぞれの考えを画面で共有することもできるので、等しい比がどれになるのかを考えていく際の参考にすることができます。

棒の長さと影の長さの割合が等しい場合を調べよう。

自力解決の様子

A　つまずいている子

・影の長さと棒の長さの関係を倍や割合で調べることができない。

Ｂ　素朴に解いている子

・影の長さと棒の長さの関係を倍や割合で求めて正しく判断している。
棒が48㎝、影が84㎝のとき、84÷48＝1.75　影は棒の1.75倍
①棒が40㎝、影が64㎝のとき、64÷40＝1.6 　影は棒の1.6倍
②棒が40㎝、影が70㎝のとき、70÷40＝1.75　影は棒の1.75倍
③棒が40㎝、影が72㎝のとき、72÷40＝1.8 　影は棒の1.8倍
だから、17時のときの図は②。

・比の値を形式的に求めて正しく判断している。
影の長さが84㎝、棒の長さが48㎝のとき、
比は　84：48　比の値　84÷48＝[MATH]\(\frac{84}{48}\)[/MATH]＝[MATH]\(\frac{7}{4}\)[/MATH]
①の比　64：40　比の値　64÷40＝[MATH]\(\frac{64}{40}\)[/MATH]＝[MATH]\(\frac{8}{5}\)[/MATH]
②の比　70：40　比の値　70÷40＝[MATH]\(\frac{70}{40}\)[/MATH]＝[MATH]\(\frac{7}{4}\)[/MATH]
③の比　72：40　比の値　72÷40＝[MATH]\(\frac{72}{40}\)[/MATH]＝[MATH]\(\frac{9}{5}\)[/MATH]
だから、17時のときの図は②。

Ｃ　ねらい通り解いている子

・｢棒の長さに対する影の長さの割合が等しいこと」と「比の値が等しいこと」を関連付け、比の値で判断すればよいことを理解している。

影の長さが84㎝、棒の長さが48㎝のとき、比の値が[MATH]\(\frac{7}{4}\)[/MATH]だから、棒の長さを１と見たときに影の長さは[MATH]\(\frac{7}{4}\)[/MATH]にあたる。②も比の値が[MATH]\(\frac{7}{4}\)[/MATH]で、棒の長さを1と見たときに影の長さが[MATH]\(\frac{7}{4}\)[/MATH]にあたる。だから、17時のときの図は②。

学び合いの計画

Ａの子供に対しては、棒が48㎝、影が84㎝の場合について、棒の長さを基にして（１と見て）、影の長さがいくつにあたるかを考えていくことを、導入で確認した数直線図を使って確認し、①～③も同じように考えるよう促します。

Ｂの子供のうち、倍や割合で考えた子供に対しては、前時で学習している比の値でも考えるよう促します。

また、比の値で考えた子供に対しては、なぜ比の値が等しいとき、同じ時刻と言えるのか、その理由を考えるよう促します。

全体の交流では、形式的に比の値で比の相等を判断するのではなく、｢比の値が等しいということは割合が等しい」ということをふまえたうえで、｢比の値が等しいときに比が等しい」というまとめにつなげていきます。

ノート例

Ｂ　素朴に解いている子

Ｃ　ねらい通りに解いている子

全体発表とそれぞれの考えの関連付け

影の長さと棒の長さの割合が、48㎝の棒のときと同じになったのは、①、②、③のどれだと思いますか。

②だと思います。

そう考えたわけを説明してもらいましょう。

〈○○さん〉48㎝の棒を基にすると、84㎝は84÷48＝1.75だから、割合は1.75です。①は影の長さが64㎝、棒の長さが40㎝だから、64÷40＝1.6。②は影の長さが70㎝、棒の長さが40㎝だから、70÷40＝1.75。③は影の長さが72㎝、棒の長さが40㎝だから、72÷40＝1.8。割合が等しいのは②です。だから、17時の図は②だと思います。

私は倍で考えました。式は○○さんと同じで、やっぱり②になりました。

比の値を使って考えた□□さんの考えを聞きましょう。

〈□□さん〉まず、48㎝の棒の場合の比の値を求めました。比は84：48だから84÷48＝[MATH]\(\frac{84}{48}\)[/MATH]で約分をして[MATH]\(\frac{7}{4}\)[/MATH]になるので、比の値は[MATH]\(\frac{7}{4}\)[/MATH]です。

そうですね。さっき割合で求めたように７÷４の商は小数だと1.75でしたが、比の値は分数で表すようにしましょう。では、①から③の比の値がいくつか、前の時間の復習もかねて、続きをほかの人にも聞いてみましょう。

※時間を与えて、隣どうしで全員に確認させてもよい。

①の比は64：40だから、64÷40を計算すると比の値は[MATH]\(\frac{9}{5}\)[/MATH]です。

②の比は70：40だから、70÷40を計算すると比の値は[MATH]\(\frac{7}{4}\)[/MATH]です。

③の比は72：40だから、72÷40を計算すると比の値は[MATH]\(\frac{9}{5}\)[/MATH]です。

比の値は正しく求められていますね。17時のときの図は①～③のどれでしょうか。

　比の値が同じなので②だと思います。

比の値が同じだとどうして②と言えるのでしょうか。この２つの[MATH]\(\frac{7}{4}\)[/MATH]が何を表しているのか、前の時間で学習した比の値の意味をふり返って、隣どうしで考えてみましょう。

※クラスの実態に応じて4名のグループにしてもよい。

まず、比の値の意味を確認しましょう。比a：ｂについて、比の値[MATH]\(\frac{a}{b}\)[/MATH]はどのような割合を表していますか。

ｂを１と見たときに、ａがいくつにあたるかを表しています。

そうですね。それでは比の値[MATH]\(\frac{7}{4}\)[/MATH]は何を表していますか。

84：48のほうは、棒の長さ48㎝を１と見たときに、影の長さ84㎝が[MATH]\(\frac{7}{4}\)[/MATH]にあたることを表しています。

70：40のほうは、棒の長さ40㎝を１と見たときに、影の長さ70㎝が[MATH]\(\frac{7}{4}\)[/MATH]にあたることを表しています。

※ほかも確認して、図に数値を書き入れる。

棒の長さと影の長さは違っていても、比の値が[MATH]\(\frac{7}{4}\)[/MATH]で等しいとき、影の長さと棒の長さの割合が同じということですね。では、今度は、次の（Ａ）から（Ｄ）の図について、影の長さと棒の長さの比が等しくなるものを、まず「比の値」を使って見当を付けましょう。見当を付けたら、棒の長さを基にした影の長さの割合を求めて、比が等しいことを確認してみましょう｡（１人１台端末で下の図を配付する。まず、個人で考えさせ、その後ペアで確認させる。必要に応じて１人１台端末で考えを共有する）

同じ時刻の図を探しましょう。

（個人やペアでの探求の時間をとった後）では、まず（Ａ）から（Ｄ）の比の値を教えてください。

（Ａ）は18÷30＝[MATH]\(\frac{18}{30}\)[/MATH]＝[MATH]\(\frac{3}{5}\)[/MATH]です。

（Ｂ）は10÷25＝[MATH]\(\frac{10}{25}\)[/MATH]＝[MATH]\(\frac{2}{5}\)[/MATH]です。

（Ｃ)は６÷８＝[MATH]\(\frac{6}{8}\)[/MATH]＝[MATH]\(\frac{3}{4}\)[/MATH]です。

（Ｄ)は９÷12＝[MATH]\(\frac{9}{12}\)[/MATH]＝[MATH]\(\frac{3}{4}\)[/MATH]です。

比の値が等しいのはどれとどれだと思いますか。

（Ｃ）と（Ｄ）です。

では､（Ｃ）と（Ｄ）の影の長さと棒の長さの割合が等しいことを確認しましょう。

（Ｃ)は比が６：８で、比の値が[MATH]\(\frac{3}{4}\)[/MATH]なので、８㎝を１と見たときに６㎝が[MATH]\(\frac{3}{4}\)[/MATH]にあたります。（Ｄ)は比が９：12で、比の値が[MATH]\(\frac{3}{4}\)[/MATH]なので、12㎝を１と見たときに９㎝が[MATH]\(\frac{3}{4}\)[/MATH]にあたります。だから、(Ｃ)と(Ｄ)の影の長さと棒の長さの割合が等しいと言えます。

この場合も、比の値が等しいときに、影の長さと棒の長さの割合が等しいことが分かりましたね。６：８と９：12のように、２つの比の値が等しいとき、割合も等しくなっています。このことを、｢２つの比は等しい」と言い、６：８＝９：12と書きます。

学習のまとめ

比が等しいかどうかは、比の値が等しいかどうかを調べれば分かる。

評価課題

次の２つの比について、等しいかどうか説明しましょう。

①　３：５と15：25 ②２：７と６：14

子供に期待する解答の具体例

①３：５の比の値　→　３÷５＝[MATH]\(\frac{3}{5}\)[/MATH]
　15：25の比の値　→　15÷25＝[MATH]\(\frac{15}{25}\)[/MATH]＝[MATH]\(\frac{3}{5}\)[/MATH]
　比の値が[MATH]\(\frac{3}{5}\)[/MATH]で等しいので、３：５と15：25の２つの比は等しい。

②２：７の比の値　→　２÷７＝[MATH]\(\frac{2}{7}\)[/MATH]
　６：14の比の値　→　６÷14＝[MATH]\(\frac{6}{14}\)[/MATH]＝[MATH]\(\frac{3}{7}\)[/MATH]
　比の値が[MATH]\(\frac{2}{7}\)[/MATH]と[MATH]\(\frac{3}{7}\)[/MATH]で等しくないので、２：７と６：14の２つの比は等しくない。