小6算数「円の面積」指導アイデア《正方形と四分円を組み合わせた形の面積》
執筆/福岡教育大学附属小倉小学校教諭・小島慶太
監修/文部科学省教科調査官・笠井健一、福岡教育大学教授・清水紀宏

目次
単元の展開
第1時 方眼を用いて、半径10㎝の円の面積の求め方を考える。
▼
第2時 半径10㎝の円を16等分した扇形を敷き詰め、既習の図形に変形させ、面積の求め方を考える。
▼
第3時 前時に等積変形させ、面積を求めたそれぞれの式から、求積公式を考える。
▼
第4時 円の[MATH]\(\frac{1}{2}\)[/MATH](半円)や円の[MATH]\(\frac{1}{4}\)[/MATH](四分円)や円と円などを組み合わせた図形の面積を求める。
▼
第5時(本時)正方形と四分円を組み合わせた形の面積の求め方を考える。
▼
第6時 形の概形を基本的な図形と捉えて、面積を概測する方法を理解する。
本時のねらい
面積の求め方が未知である図形の構成を捉え、筋道立てて面積を求める方法を考え、説明することができる。
評価規準
既習の図形の求め方を活用して、円と正方形、長方形からなる複合図形の面積を求め、説明することができる。(思考力・判断力・表現力)
本時の展開
この図形をどうやってかいたと思いますか。
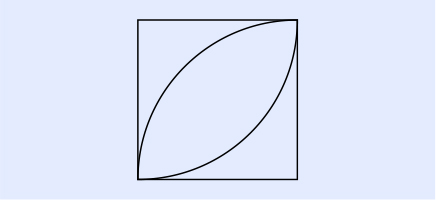
正方形をかいて、その後コンパスを使ってかいたと思います。
そうですね(黒板の図でコンパスで弧をなぞる)。この図には、いろいろな形が見えます。どんな形が見えますか。
前の時間に面積を求めた「[MATH]\(\frac{1}{4}\)[/MATH]の円」が見えます。
※「[MATH]\(\frac{1}{4}\)[/MATH]の円」「四分円」など、前の時間に名前を付けておくとよい。
※黒板の図を子供に「なぞって」確認させる。
[MATH]\(\frac{1}{4}\)[/MATH]の円がもう1つあります。
※黒板の図を子供に「なぞって」確認させる。
では、今日の問題です。

色のついたところの面積を求めましょう。
色のついた形は、どんな形に見えますか。
オムライスに見えます。
ラグビーボールにも見えます。
いろいろありますね。今日は、これをオムライスの形ということにしましょう。このオムライスの形の面積の求め方を考えます。これまで学習したことが使えそうですか。
正方形の面積が使えそうです
[MATH]\(\frac{1}{4}\)[/MATH]の円の面積が使えそうです。
正方形や[MATH]\(\frac{1}{4}\)[/MATH]の円を求めるだけで、オムライスの形の面積は出せそうですか。
求めた面積を足したり、引いたりしないといけないと思います
それでは、面積の求め方を考えましょう。式だけでなく、どの形とどの形を足したり引いたりしたのか、友達に分かるように、言葉や図の説明も考えましょう。

オムライスの形の面積の求め方を考え、図や言葉で説明しよう。
導入では、この図形がどのような図形で構成されているかを確認します。子供に発言させるだけでなく、黒板の図で正方形、おうぎの形を実際になぞらせることで確実に確認します。そして、既習の図形を組み合わせてオムライスの形の面積を求めるという見通しにつなげます。
本時では、式と答えだけ書かせるのではなく、「友達に分かるように」という条件を付けることで、図や言葉で表現することもねらいます。
なお、この教材の扱いは教科書でまちまちです。教科書に紹介されている「[MATH]\(\frac{1}{4}\)[/MATH]の円から三角形を引き、2倍する方法」は子供が自力で思い付くのは難しいので、導入でヒントを与えるか、本提案のように問題②として扱うとよいでしょう。
また、「2つの[MATH]\(\frac{1}{4}\)[/MATH]の円の面積の和から正方形の面積を引く方法」は難しいので、子供の実態に応じて取り扱うかどうかを判断しましょう。
例えば、[MATH]\(\frac{1}{4}\)[/MATH]の円を透明な色のセロファンで用意して重ねて見せたり、デジタル教材で見せたりして、その考え方に触れるという程度でもよいでしょう。
見通し
<使えそうな形> ・正方形 ・おうぎの形(2つ)
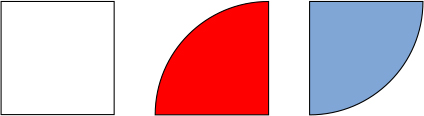
<方法> ・図形の面積を合わせる、引く。
自力解決の様子
A つまずいている子
・正方形や[MATH]\(\frac{1}{4}\)[/MATH]の円の面積を求めているが、それらを適切に組み合わせることができない。
B 素朴に解いている子
・正しい答えを導いているが、式だけの表現にとどまっている。
(式)
10×10=100
10×10×3.14÷4=78.5
100-78.5=21.5
100-21.5-21.5=57 答え57㎠
C ねらい通り解いている子
・図や言葉で考えを説明することができている。
(言葉と式)
まず、[MATH]\(\frac{1}{4}\)[/MATH]の円の面積を求めます。
10×10×3.14÷4=78.5
次に、正方形から[MATH]\(\frac{1}{4}\)[/MATH]の円を引いた残りの面積を求めます。
100-78.5=21.5
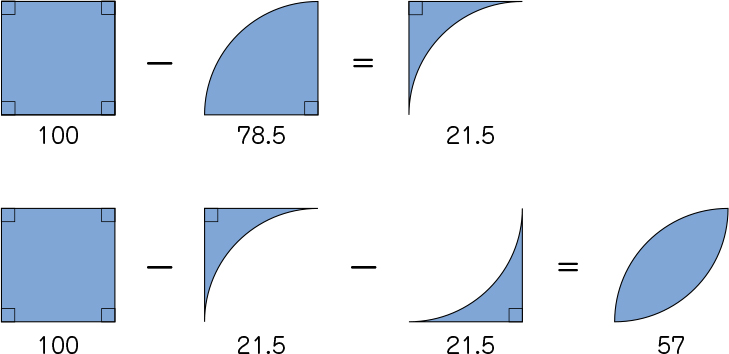
最後に、正方形の面積から残りの面積2つ分を引くとオムライスの形の面積になります。
100-21.5-21.5=57 答え57㎠
<図と式>
学び合いの計画
Aの子供には、オムライスの形の面積が正方形から「正方形から[MATH]\(\frac{1}{4}\)[/MATH]の円を除いた部分」2つ分を除いてできることを確認し、「正方形から[MATH]\(\frac{1}{4}\)[/MATH]の円を除いた部分」の面積を求めることを促します。
[MATH]\(\frac{1}{4}\)[/MATH]の円の面積を求めることができれば、このことには、比較的多くの子供が取り組むことができると考えられます。[MATH]\(\frac{1}{4}\)[/MATH]の円の面積を求めることができない子供には個別に指導しましょう。
Bの子供は、式をかいて正答にも至っているので、図形の構成について理解していると言えます。
これに加えて、解き方を言葉や図で説明することを促します。例えば、100-78.5=21.5という式について、「何から何を引いたのか、言葉や図でかいてごらん」といった指示をすることが考えられます。
本時の題材については、「[MATH]\(\frac{1}{4}\)[/MATH]の円」や「正方形から[MATH]\(\frac{1}{4}\)[/MATH]の円を除いた部分」といった表現が煩雑なので、図による説明でも十分でしょう。
あるいは、「正方形から[MATH]\(\frac{1}{4}\)[/MATH]の円を除いた部分」を「へこんだ形」「ブーメラン」「残りの部分」のように、そのクラスで共有できる名前を付けることができれば説明しやすくなります。オムライスの形をⒶ、「正方形から[MATH]\(\frac{1}{4}\)[/MATH]の円を除いた形」をⒷなどと記号で表す方法もあります。
全体の交流では、「『正方形から[MATH]\(\frac{1}{4}\)[/MATH]の円を除いた部分』の2つ分の面積を正方形の面積から引く方法」(正方形の面積からへこんだ二等辺三角形2つ分の面積を引く方法)の解法と表現をていねいに扱いましょう。
次に、正方形の対角線を補助線として引く図を提示し、子供とやりとりしながら図の構成を捉え、ペアで考えさせます。その後、余裕があれば、[MATH]\(\frac{1}{4}\)[/MATH]の円の2つ分の面積から正方形の面積を引く方法を紹介します。
以上の求め方をふり返り、どのような図形を使ったのかを確認するとともに、本時で扱ったような[MATH]\(\frac{1}{4}\)[/MATH]の円でできた図形でも、面積の求め方を知っている図形を組み合わせたり、引いたりして求めることができるというまとめにつなげます。
ノート例
※赤字でかかれている所は、解決方法の共有や交流のなかで付加・修正してかいたものです。
B 素朴に解いている子
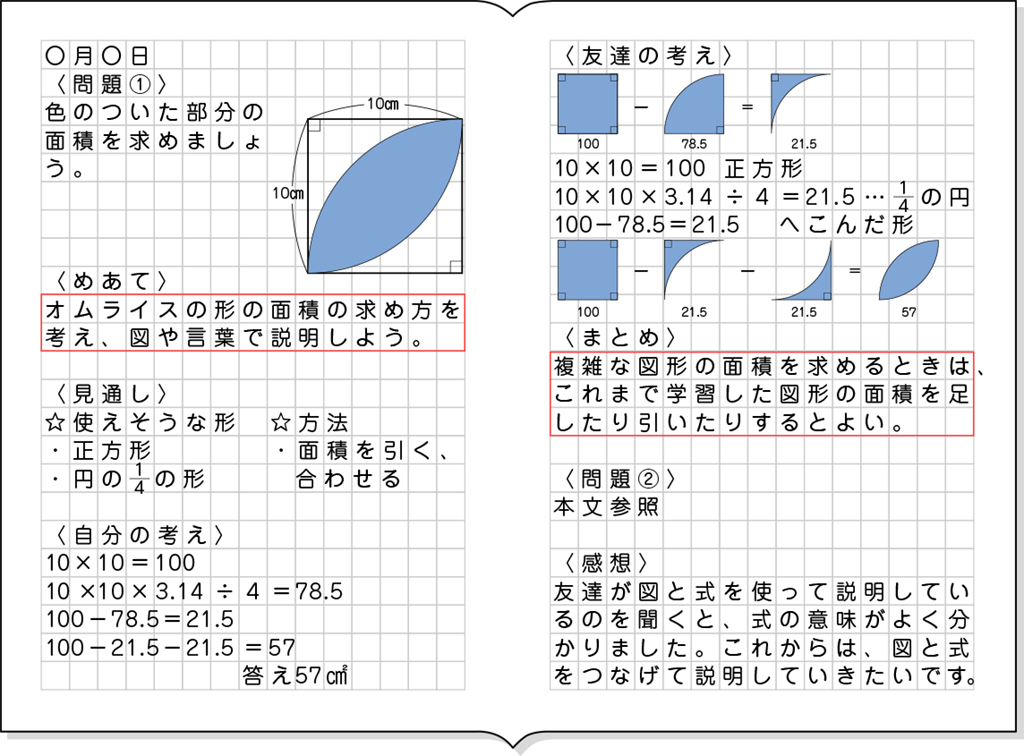
C ねらい通り解いている子
イラスト/横井智美

