小3算数「かけ算」指導アイデア《かける数/かけられる数が0の場合のかけ算》

執筆/東京都台東区立浅草小学校教諭・横須賀咲子
監修/文部科学省教科調査官・笠井健一、東京都目黒区立八雲小学校校長・長谷豊

目次
単元の展開
第1時 乗法の性質やきまりに着目して九九の答えの見付け方を考える。
▼
第2時 乗法の分配法則(被乗数を分解)に着目して、九九の答えの求め方を考える。
▼
第3時 乗法の分配法則(乗数を分解)に着目して、九九の答えの求め方を考える。
▼
第4時 乗法の性質やきまりに着目して、被乗数や乗数が10のときの答えの求め方を考える。
▼
第5時 乗法の性質やきまりに着目して、被乗数が10を超える場合の答えの求め方を考える。
▼
第6時(本時)被乗数や乗数が0になるときの乗法の式について考える。
▼
第7時 被乗数または乗数が未知数の式を、九九を用いて未知数を求める。
▼
第8時 まとめ
本時のねらい
被乗数や乗数が0の場合の式の意味を理解し、計算の答えを求めることができる。
評価規準
- 0を含む乗法の式の意味を理解し、計算の答えを求めることができる。(知識・技能)
- 乗法に関して成り立つ性質などを用いて、被乗数や乗数が0の場合の乗法の答えが0になることを説明している。(思考・判断・表現)
本時の展開
おはじきゲームをします。おはじきを指で弾いて、どこに入ったかで得点が決まります。得点板から出てしまったら0点です。1人10回弾いて、合計の得点で勝敗が決まります。
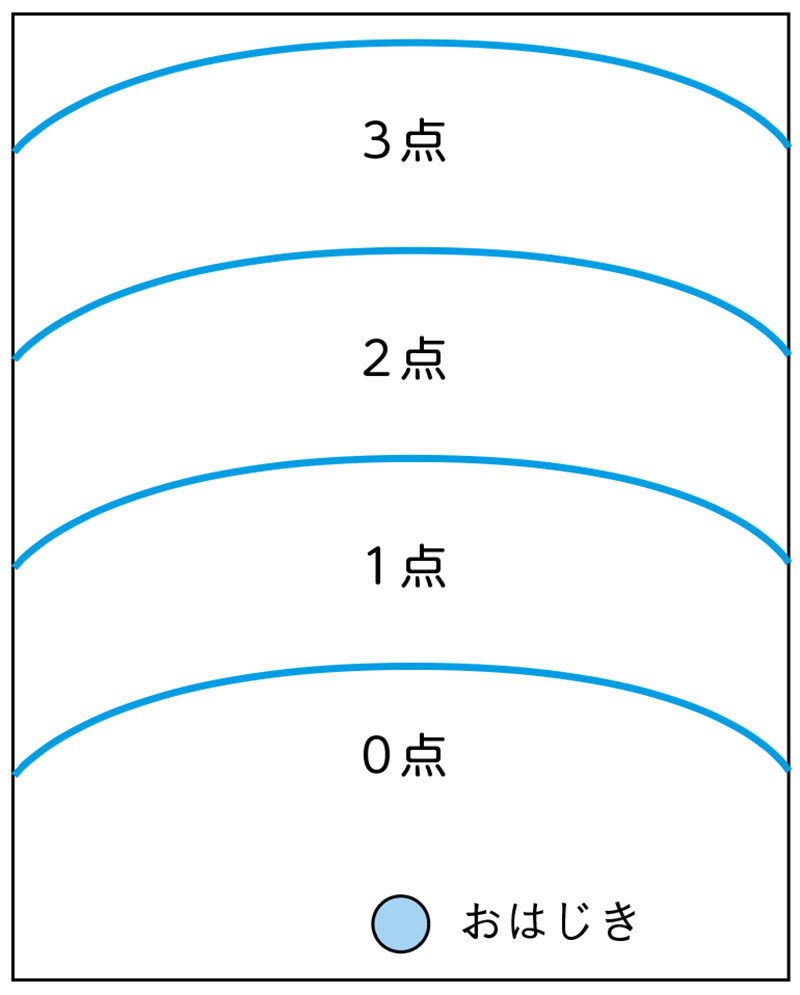
試しに先生がやってみたら、このような結果になりました。

3点ゾーンに1回も入っていません。
0点ゾーンに4回も行っています。
先生の2点ゾーンの得点の取り方を式に表すとどうなりますか。
2点が4回なので、2×4です。
そうですね。得点は何点ですか。
2×4で8点です。
そうですね。では、1点ゾーンのところは、どうですか。
1点が2回なので、1×2で2点です。

被乗数や乗数が0の場合の意味を理解する。
3点ゾーンの得点の取り方は、式に表すとどうなりますか。ノートに式を書いてみましょう。隣の席の友達と、どうしてその式になるのか、話し合ってみましょう。
どんな式になりましたか。そして、それはどうしてですか。
3×0だと思います。2点ゾーンのときに、2点が4回だから2×4でした。3点が0回だから、3×0だと思います。
私も3×0だと思います。もしも3点が1回だったら3×1、3点が2回だったら3×2、3点が3回だったら3×3……です。順番に考えていくと、1回も取っていないから3×0です。
式は3×0で表せますね。3×0の答えはどうなりますか。ノートに答えを書いてみましょう。隣の席の友達と、3×0の答えを伝え合ってみましょう。
僕と隣の人で答えが違ってしまいました。僕は3だと思ったんだけど、隣の人は0でした。
私は0だと思います。3点を1回も取っていないから、3点は入らないと思います。
さっき、3×1、3×2……と順番にやっていて、3の段は掛ける数が1つ増えると3ずつ増えていました。それで、3×0は3×1のひとつ前だから、3減らして0になると思います。
3点ゾーンの得点は、3×0=0でいいですね。では、0点ゾーンの得点の取り方を式に表すと、どうなるでしょう。
さっきと同じで4×0だと思います。
0点が4回だから0×4だと思います。
0+0+0+0と同じだから0×4だと思います。
そうか。0×4だと分かりました。
0×4の答えはどうなりますか。
0点は何回取っても0点だから、0だと思います。
さっきと同じように考えると、3×4=12、2×4=8、1×4=4と4ずつ減っているから、0×4も4減って0です。
0点ゾーンの得点は、0×4=0になりますね。

得点の取り方を式に表して、得点を計算することができる。
では、隣の席の友達とおはじきゲームで勝負をします。ゲームは10回戦です。自分の得点の取り方を式に表して、得点の合計を求めましょう。また、どうしてそうなるのかわけも書きましょう。
※隣どうしでゲームを行う。
自力解決の様子
A つまずいている子
3×2=6
2×2=4
1×0=1
0×6=6
合計17点
※0を含む乗法の計算を間違えている。
3×2=6
2×2=4
合計10点
※0点ゾーンや0回のところの式を立てていない。
B 素朴に解いている子
3×2=6
2×2=4
1×0=0
0×6=0
合計10点
C ねらい通り解いている子
それぞれの式の意味も説明できている。
学び合いの計画
イラスト/横井智美

