小5算数「正多角形と円」指導アイデア《円周と直径の関係を調べ、円周率を理解しよう》
執筆/新潟県公立小学校教諭・竹内直也
編集委員/文部科学省教科調査官・笠井健一、新潟県公立小学校校長・間嶋哲
目次
本時のねらいと評価規準(本時の位置 6/9時)
ねらい
円の直径と円周の関係について、具体物を用いて調べた円周と直径の長さを表にまとめ考察することを通して、どんな大きさの円でも(円周)÷(直径)は約3.14となることがわかる。
評価規準
任意の円を用いて円周と直径の長さを測り、それらの値を基に(円周)÷(直径)は約3.14になることを説明している。
問題場面
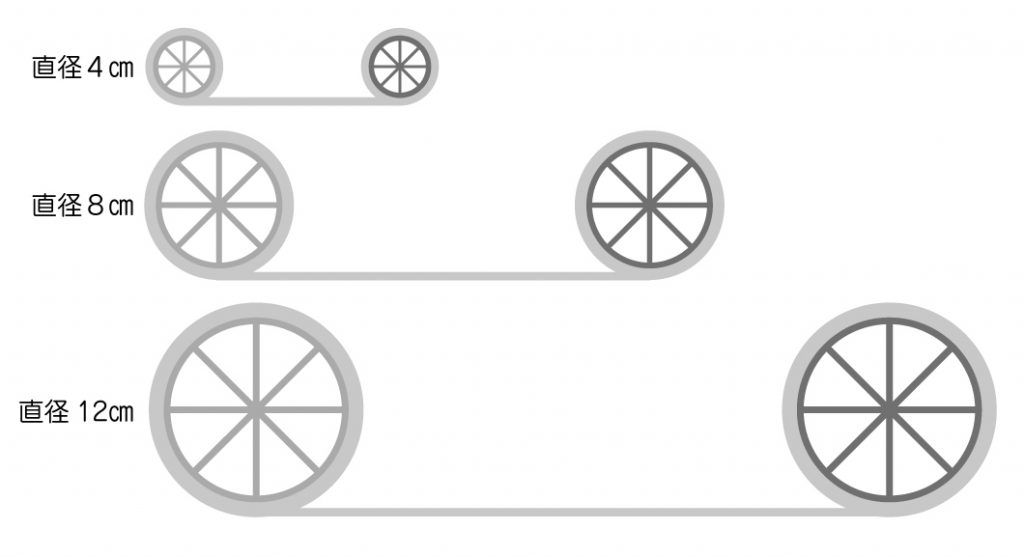
大きさの異なる車輪が3つあります。これらの車輪が1回転するときの距離を調べましょう。
拡大した車輪の模型やアニメーションソフトを用いて車輪が1回転する様子を示し、車輪の幅が「直径」、車輪が1回転するときの距離が「円周」の長さにあたることを捉えさせます。その後、厚紙で作った3つの車輪の直径と円周の長さを実測させます。
1回転すると、こんなに進むのかぁ。
実際に測ってみましょう!
実測値には誤差が生じるため、車輪ア・イ・ウをそれぞれ分担して実測させるなど、混乱を避けるための工夫をします。
大きい車輪は進む距離が長いから、円周の長さが長いってことだよね。
円周の長さと直径に、なにかきまりがありそうだよ。
本時の学習のねらい
円周と直径の長さには、どんな関係があるのだろうか。
見通し
直径は2倍、3倍になっている。円周は何倍になっているか調べると、きまりが分かりそうだよ。
円周の長さは直径に比べてだいぶ長くなっているよ。何倍になっているか調べてみよう。
自力解決の様子
A つまずいている子
直径が長くなれば、円周の長さも長くなることは理解しているが、円周の長さと直径との規則性は見いだせない。
B 素朴に解いている子
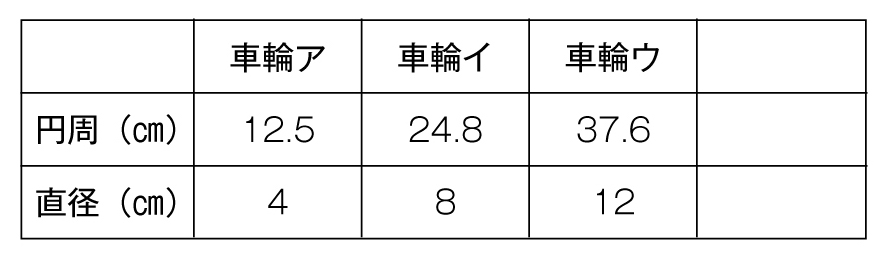
表を横に見ることで、直径が2倍、3倍…になれば、円周の長さも2倍、3倍…になること(比例関係)に気付き、計算によって確かめている。
C ねらい通り解いている子
比例関係に気付くとともに、表を縦に見て、円周の長さが直径のおよそ3倍になっていることを計算によって見いだしている。
学び合いの計画
イラスト/横井智美
『教育技術 小五小六』 2022年2/3月号より