小5算数「図形の合同と角」指導アイデア《合同な三角形のかき方》

特集: 【文部科学省教科調査官監修】1人1台端末時代の｢教科指導のヒントとアイデア｣

2022.08.15

単元の展開

第１時　図形を重ね合わせる操作を通して、合同の意味を理解する。
▼
第２時　合同な二つの図形の対応する辺の長さや角の大きさが等しいことを理解する。
▼
第３時　長方形や平行四辺形、台形を対角線で分けてできた三角形を合同の観点で考察する。
▼
第４時（本時）図形の構成要素に着目し、合同な三角形のかき方を考え、作図する。
▼
第５時　合同な三角形を三つの方法で作図する。（技能の習熟）
▼
第６時　合同な三角形の作図のしかたを基に、合同な四角形のかき方を考え、作図する。
▼
第７時　合同な三角形の敷き詰めを通して、内角の和が180°であることを理解する。
▼
第８時　三角形の内角の和が180°であることを基に、四角形の内角の和を調べる。
▼
第９時　三角形や四角形の内角の和を基にして、多角形の内角の和を調べる。

本時のねらい

図形の構成要素に着目して、合同な三角形のかき方を考え、作図することができる。

評価規準

三角形の構成要素に着目しながら、合同な三角形のかき方を説明している。

本時の展開

次の三角形ABCと合同な三角形をかきましょう。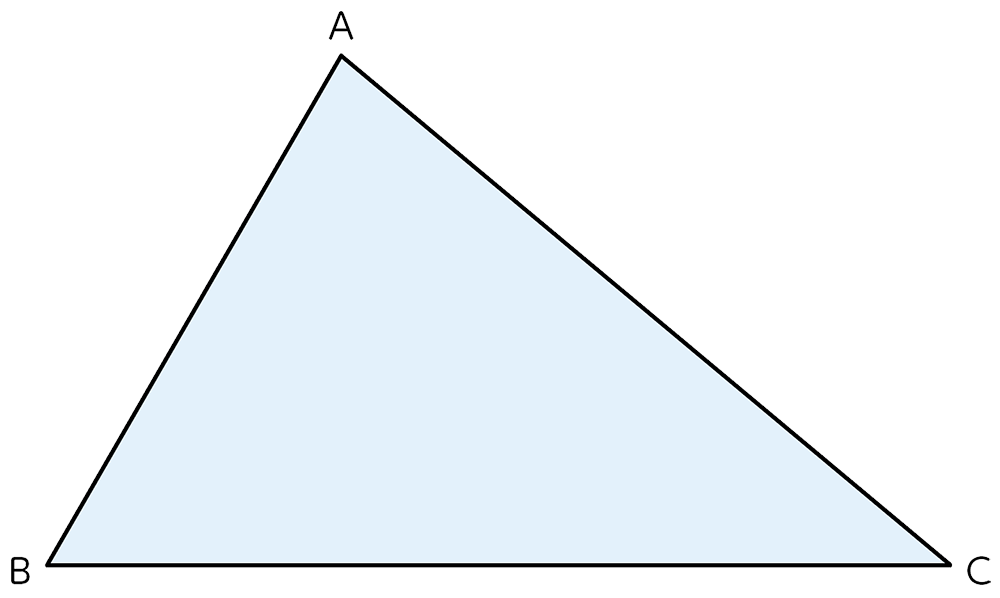

※実寸の図形を印刷したプリントを数値は書き込まずに子供たちに配付します。板書用は大きく拡大したものを用意し、子供たちと対話しながら数値を書き込んでいきます。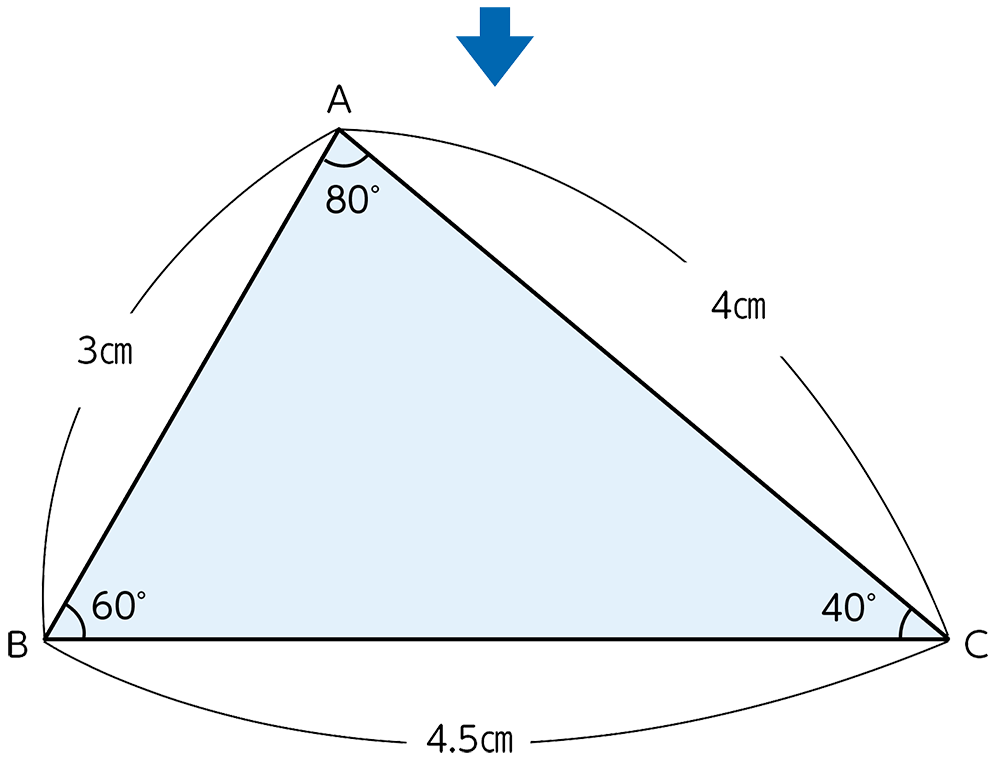

合同な図形の特徴について覚えていますか。

対応する辺の長さが等しく、対応する角の大きさも等しいです。

そうですね。では、今日は合同な三角形をかいてみましょう。はじめに頂点Bをつくりましょう。次に頂点Cをつくりましょう。どこに頂点Cをつくればよいですか。

辺BCの長さが分かればできます。

頂点Bと頂点Cまでは4.5㎝だ。対応する辺の長さは等しいから、頂点Bから4.5㎝離して、頂点Cをつくればいいね。

※子供に辺BCの長さを計測させた後、板書用の図形に数値を書き込み、一緒に辺BCをつくっていきます。

頂点Bと頂点Cができたら頂点どうしを結んで辺BCをつくりましょう。最後に、頂点Aをつくったら完成ですね。どうすれば頂点Aをつくることができるでしょうか。グループで相談してみましょう（ここで本時の課題を焦点化します）。

辺ABと辺ACの長さが分かれば、頂点Aがつくれると思います。

角Bの大きさと辺ABの長さが分かれば、頂点Aがつくれると思います。

四年生の角の大きさの学習で三角形をかいたとき、角Bと角Cを使って三角形をかいたから……、角Bと角Cの大きさが分かればできそうです。

すべての辺の長さや角の大きさは使わなくてもよさそうですね。なるべく少ない手順でかけるといいですね。

※子供の発言に合わせながら、適宜、辺の長さや角の大きさを確認し、板書用の図形に数値を書き込みましょう。数値にズレがあると子供が混乱するため、全体で確認しておくことが大切です。また、子供にどの構成要素を使えばよいのか、思考させていくことにもつながります。

頂点Aをつくるには、どの辺の長さや角の大きさが必要かを考え、なるべく少ない手順で合同な三角形をかこう。

見通し

この学習は単元を通して、子供たちに図形の構成要素である頂点、辺、角を常に意識させることが大切です。

作図の学習では、「はじめに底辺を引きましょう。そして、次に……」といったような作図のためのスキルを習得させることに終始してはいけません。子供が「どの構成要素が定まれば、条件を少なく、三角形を一つに決定できるのか」ということを思考することに、学習の価値があります。

問題に出合わせた後、まず、合同な図形の特徴を問うことで、対応する辺や角、頂点に着目させていきます。そして、頂点から辺ができることを意識させるために、頂点Bと頂点Cをとらせます。このとき、辺の長さの数値を子供自らが知りたがるように、情報不足の状態で提示しておきましょう。

子供とやりとりをしながら、辺BCをつくり、その後、「頂点Aをつくるには……」と問うことで、頂点Aの決め方を考えるという課題に焦点化させていきます。このとき、小集団の交流を仕組んで、子供たちからアイデアを集約していくとよいでしょう。

自力解決の様子

A つまずいている子

角度を考えずに、頂点Bから3㎝の辺を斜めに引いている。

頂点Bから頂点A までは3㎝だから……。

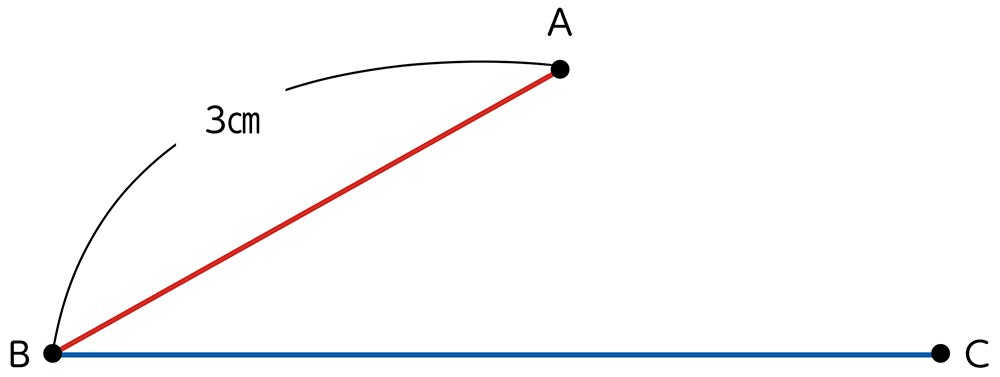
Ｂ素朴に解いている子

合同な三角形はできているが、角度や辺の長さを四つ以上使ってかいている。

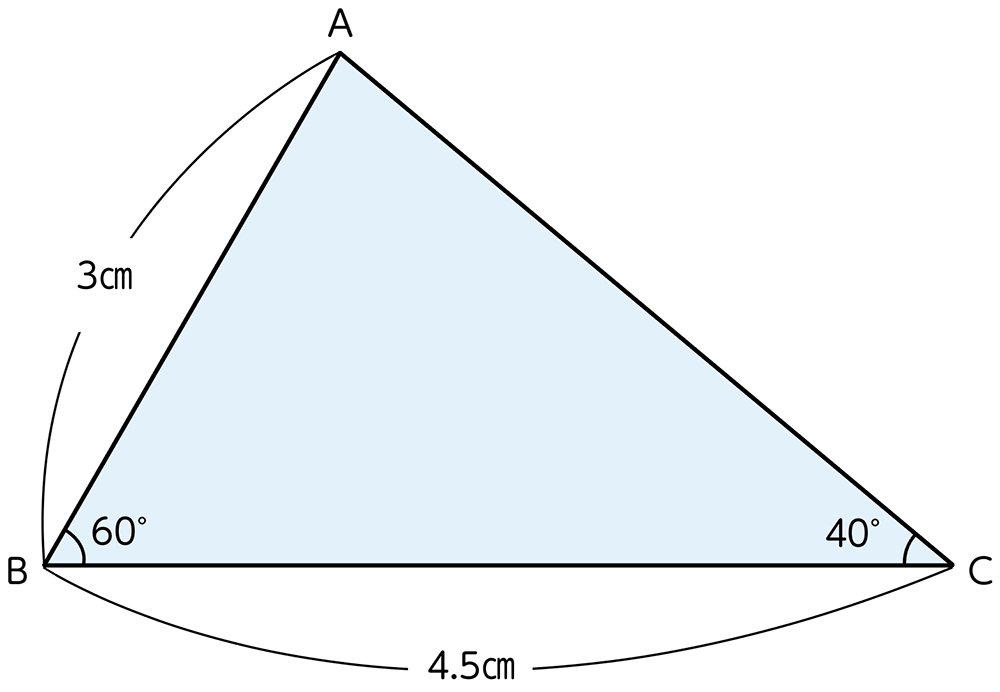
Ｃねらい通り解いている子

三つの構成要素を使ったいずれかのかき方で、合同な三角形をかいている。

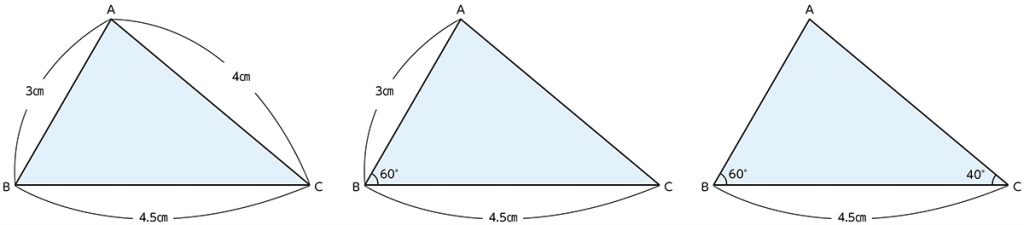
※自力解決させていくときは、作図した三角形が本当に合同になっているのか、子供自身に対応する辺の長さや対応する角の大きさを測定させ、確かめさせることを忘れないようにしましょう。

学び合いの計画

自力解決では、Ａの子のように、辺の長さだけに着目して行き詰まってしまう子供がいるかもしれません。

教師による指導としては、Ａの子に対して、角Bの大きさが60°ではないことに気付かせ、正しい大きさの角Bを分度器でつくるよう促すことなどが考えられます。

また、小集団の交流を位置付けることも考えられます。辺の長さや角の大きさを友達どうしで確かめるように指示をしておくことで、Ａの子のようにつまずいている子供が、友達とのやりとりのなかで、作図に必要な構成要素に気付いていくかもしれません。

小集団の交流

では、お互いの考えを説明して合同になっているのか、確認していきましょう。

僕は、ここまではかけたんだけど……。

なるほど。確かに辺ABは3㎝になっているけど、角Bの大きさが違うよ。合同な三角形は対応する角の大きさも同じじゃないといけないから……。

あっ。そういうことか。角Bは60°にならないといけないのか。角度のことは考えていなかったよ。

じゃあ、角Ｂを60°にしてかき直してみようよ。

ノート例

Ａつまずいている子

Ｂ素朴に解いている子

全体発表とそれぞれの考えの関連付け

その後、全体交流①を行っていきます。全体交流①のなかでは、Ａの子のような考えやＢの子のような構成要素が三つよりも多い考えを取り上げ、必要な構成要素について考えさせていきます。

全体交流①（Ａの子の考えについて）

皆さん、いろいろなかき方で合同な三角形ができていましたが、うまくいかない場合もありました。この三角形についてどのように思いますか。

角Bの角度が違うように見えます。

かきたい三角形ではABがACより短いのに、この三角形では辺ABのほうが長くなっています。

（角Bが60度でないことなどを確認した後）、それではどのように直せばよいでしょうか。

先に60度の角をかいておいて、それから3㎝を測ればよいと思います（ICTなどを活用して、この作図のここまでの手順を確認する）。

だったら、角Cの40度を先にかいておいて、ACの4㎝をかく方法もあります。

それでは、どちらかの方法で三角形ABCをかいてみましょう。かいたら、隣の人どうしで、かけているか確認しましょう。

全体交流①（Bの子の考えについて）

では、これはどうでしょう。合同な三角形はできています。次のような手順でかいています。

・角Bを60度でかく　→　ABを3㎝でかく　→　角Cを60度でかく（実際に手順を見せる）

この手順を見て、何か気付いたことはありますか。

手順が多いと思います。

さっきの方法と同じようにかいていると思いませんか。

角Cの大きさを測らなくても、AとCをつなげばよいと思います。

私はABの長さと角Bの大きさだけ測って、頂点Aをつくれました。

角Cの大きさは使わなくてもかけそうですね。

ほかにもあります。角Bと角Cの大きさが分かっていれば頂点Aがつくれるので、辺ABの長さは使わなくてよいです。

（実際に手順を確認する）

全体交流②

次に全体交流②を行います。全体交流②では、子供たちにいくつの構成要素を使ったかを問い、一番少ないのは三つであることを確認します。

このとき、三つの構成要素で作図した子供たちの考えを何人分か、写真に撮って集約しておきましょう。その考えをスクリーンやモニターに映したり、子供たちのタブレットに配信したりして、再び小集団交流を行い、考えを３種類のグループに仲間分けさせていきます。

その後、もう一度全体で交流をして合同な三角形の三つのかき方をまとめていきます。交流中は、子供の説明に合わせて辺や角に色を付け、視覚的に捉えやすくしていくとよいでしょう。

また、交流の最後に三つの構成要素を使ってもかけない事例を出すと理解がより深まると思います。

今、皆さんのタブレットに辺や角の大きさのなかから三つだけ使って合同な三角形をかいた考え方を送りました。これらの考えを３人組で話しながら、仲間分けしてみましょう。

いくつのグループに分けられましたか。

三つの考え方に分けることができました。

この考えは三つの辺だけを使ってかいています。

三つの辺だけですか。三つの辺でどうやってかいたのでしょうか。

まず、底辺BCをかきます。次に残った二つの辺の長さをコンパスで測って、交差したところを頂点Aにします。後は頂点を結んでいくと完成です。

※子供の説明に合わせて教師用のタブレットの図や板書用の拡大図の辺に色を付けて、手順が視覚的に捉えられるようにします。

なるほど。三つの辺を使ったかき方ですね。

次の考えは二つの辺とその間の角の大きさを使っています。底辺BCをかいて、その後、角Bの大きさを測って線を引き、長さの３㎝のところを頂点Aにします。最後に頂点Aと頂点Cをつなぎます。

最後は一つの辺とその両側の角の大きさを使う考えです。底辺BCをかいた後、両側の角の大きさを測って直線を伸ばします。直線が交差したところが頂点Aです。

合同な三角形をかく方法は、「三つの辺」「二つの辺とその間の角」「一つの辺とその両側の角」という三種類のかき方があるのですね。では、どれも辺の長さや角の大きさから三つだけを使っていますが、この三つでもかくことができますか。

ん？　いや、これではかけない。三つと言っても、どこでもいいわけではないのか。

全部の辺の長さや角の大きさが分からなくても、辺の長さや角の大きさから三つが分かると、合同な三角形をかくことができる（３辺・２辺とその間の角・１辺とその両側の角）。
学習のまとめでは、三つの構成要素が定まれば三つの頂点が決まり、作図することができることに気付かせます。「作図は頂点をつくっていく」「すべての辺の長さや角の大きさを調べなくてよい」という意識を、子供も教師ももっておくことが大切です。