小6算数「分数×分数」指導アイデア《乗数の分子が１以外のときの分数×分数の計算》

特集: 文部科学省教科調査官監修｢教科指導のヒントとアイデア｣

2022.04.15

単元の展開

第１時　乗数の分子が１のときの（分数）×（分数）の計算のしかたを考える。
▼
第２時（本時）乗数の分子が１以外のときの（分数）×（分数）の計算のしかたを考える。
▼
第３時　乗数が仮分数の計算のしかたを考える。
▼
第４時　帯分数や整数が入った分数のかけ算の計算のしかたを考える。
▼
第５時　（小数）×（分数）、（分数）×（小数）の計算のしかたを考える。
▼
第６時　１より小さい分数をかけると、積は被乗数より小さくなることを理解する。
▼
第７時　（分数）×（分数）×（分数）の計算のしかたを考える。
▼
第８時　長さが分数で表されている長方形の面積と直方体の体積を求める。
▼
第９時　交換法則や結合法則、分配法則が、分数の計算にも適用できるか考える。
▼
第10時　積が１になる乗数を見付け、被乗数の乗数との間のきまりを見付ける。
▼
第11時　練習問題を解き、学習内容の理解を深める。

本時のねらい

分数×分数について、図や数直線を用いて表すことを通して、単位分数の見方で捉えたり、（分数）×（整数）、（分数）÷（整数）を活用したりして、計算することができる。

評価規準

分数×分数の場面について、単位分数の見方で捉えたり、（分数）×（整数）、（分数）÷（整数）を活用したりして、計算することができる。

へいにペンキをぬります。このペンキは、１dLあたり[MATH]\(\frac{4}{5}\)[/MATH]㎡ぬれます。このペンキ[MATH]\(\frac{2}{3}\)[/MATH]dLでは、なん㎡ぬれますか。

前時との違いを意識化させるためにも、下線部（[MATH]\(\frac{2}{3}\)[/MATH]dL）を提示する前に、「どんな数だったらいい？」と予想させる活動を入れましょう。

前回の問題より難しそうですか。難しいという人はグー、簡単という人はパーを挙げましょう。

前回の算数と変わらないです。

今回のほうが難しい。

難しいと言っている人もいるけれど、どこが難しそうですか。

前回は、[MATH]\(\frac{4}{5}\)[/MATH]×[MATH]\(\frac{1}{3}\)[/MATH]でした。今回は[MATH]\(\frac{4}{5}\)[/MATH]×[MATH]\(\frac{2}{3}\)[/MATH]で、かける数の分子が２になっているから、難しいと思います。

分子が１じゃないと、どうやって計算すればいいか分かりません。

かける数の分子が１でない分数のかけ算は、どのように計算すればよいか。

見通し

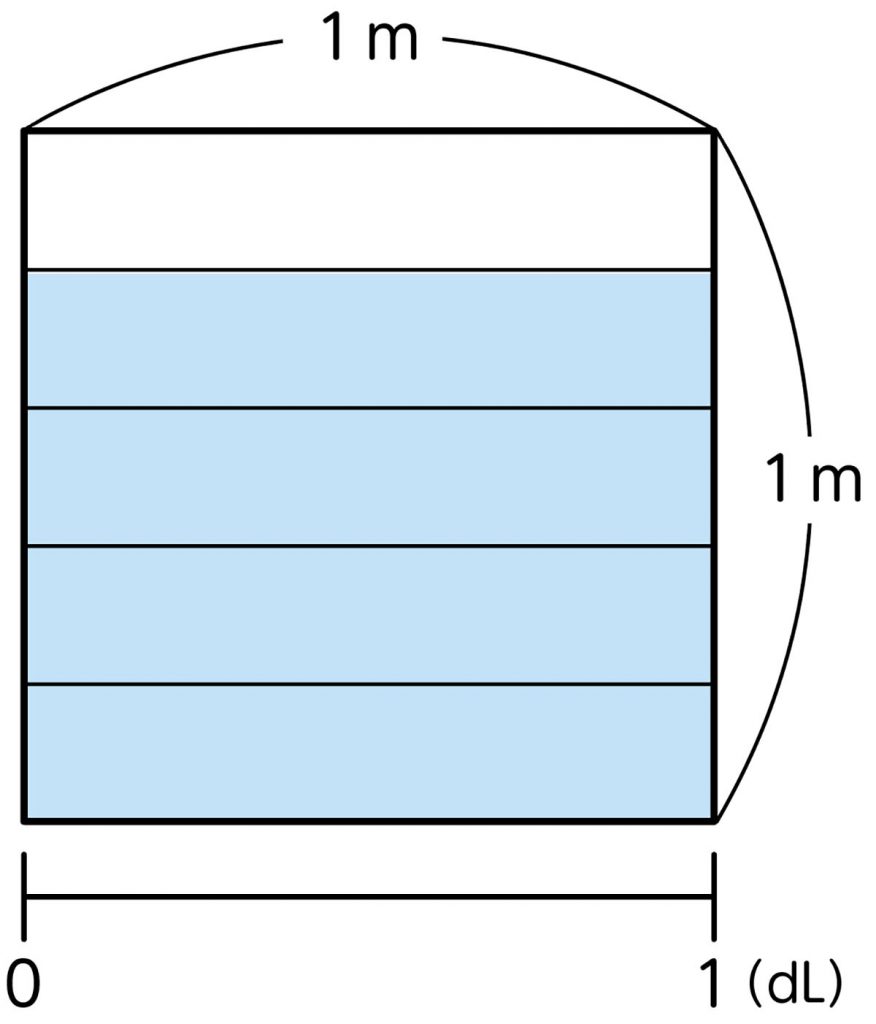
図で言うと、[MATH]\(\frac{4}{5}\)[/MATH]×[MATH]\(\frac{2}{3}\)[/MATH]はどのくらいだと思いますか。タブレットの図に色を塗りましょう。

１人１台端末活用ポイント

タブレットで面積図を配付し、子供に答えの部分はどこになりそうか色を塗らせます。その際、色を塗った部分の理由も考えさせましょう。その後、全体で共有することにより、これからどの部分の面積を求めればよいのか、結果の見通しをもてます。

３つに分けたうちの２つ分だから、これくらいかな。

かける数の分子が１じゃなくて困っていたけれど、どうすれば計算できたり、考えられたりしそうですか。

数直線で表します。

×分数を整数に直して計算します。

[MATH]\(\frac{1}{3}\)[/MATH]dLが分かれば、[MATH]\(\frac{2}{3}\)[/MATH]dLも計算できると思います。

前回の[MATH]\(\frac{1}{3}\)[/MATH]dLのときを２倍にします。

[MATH]\(\frac{4}{5}\)[/MATH]×[MATH]\(\frac{2}{3}\)[/MATH]のやり方を数直線や図、計算で考えましょう。

自力解決の様子

A つまずいている子

図から考える。
[MATH]\(\frac{8}{10}\)[/MATH]

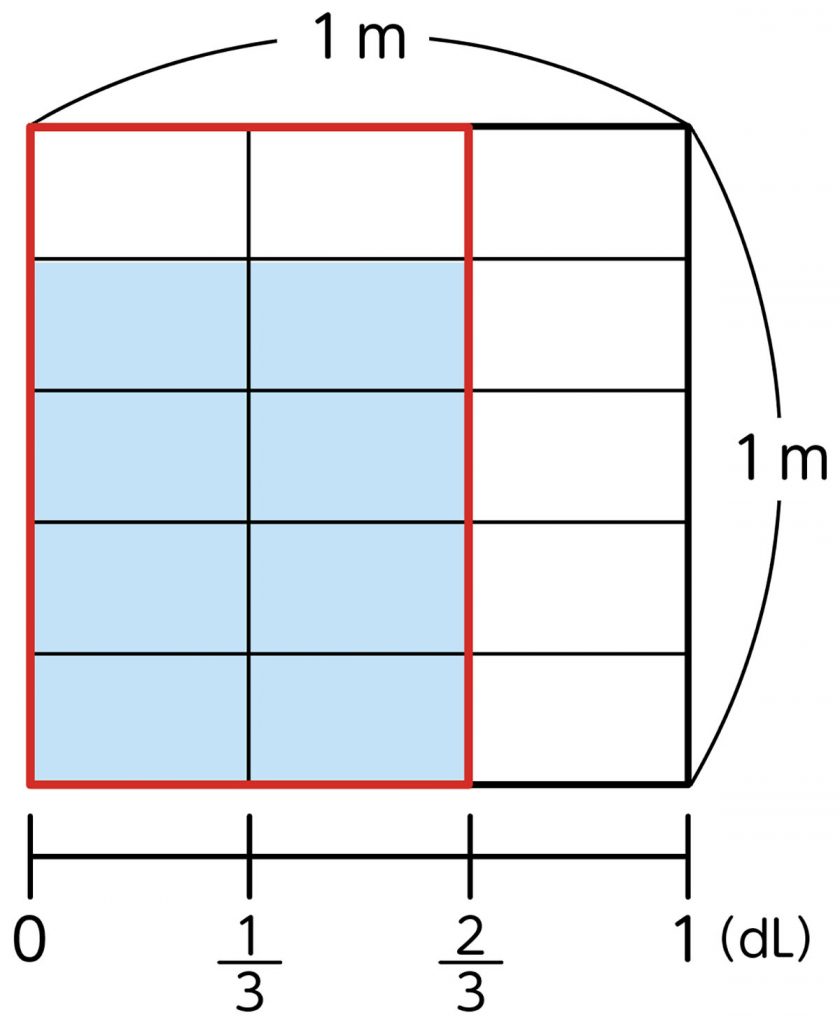
基にする量が曖昧になり、分母を捉え違えたり、分数に表す方法が分からなくなる子供が想定されます。机間指導の際に、Aの子供を見とり、必要があれば何を分けているのか問いかけたり、学び合いでＢやＣの子供とかかわれるようにグルーピングしたりしましょう。

Ｂ素朴に解いている子

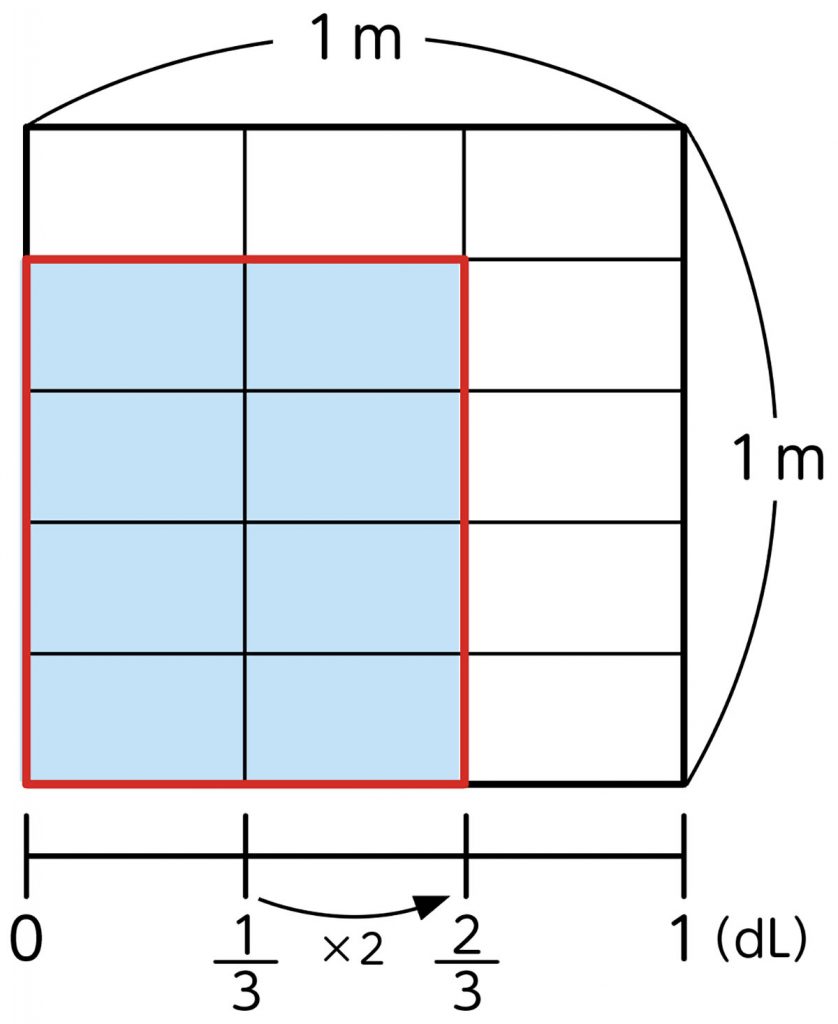
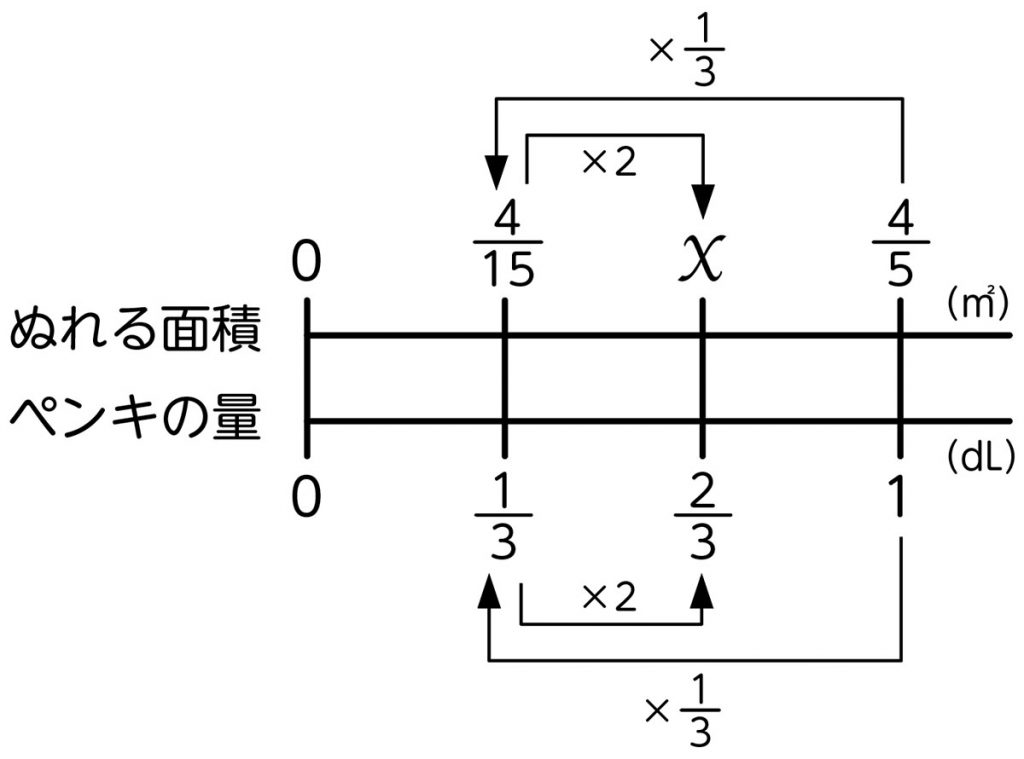
前時を生かす。
[MATH]\(\frac{4}{5}\)[/MATH]×[MATH]\(\frac{1}{3}\)[/MATH]＝[MATH]\(\frac{4}{15}\)[/MATH]だったから、答えを２倍すればよい。
[MATH]\(\frac{4}{5}\)[/MATH]×[MATH]\(\frac{2}{3}\)[/MATH]＝[MATH]\(\frac{4}{15}\)[/MATH]×２＝[MATH]\(\frac{8}{15}\)[/MATH]

Ｃねらい通り解いている子

C1　単位面積を考える。
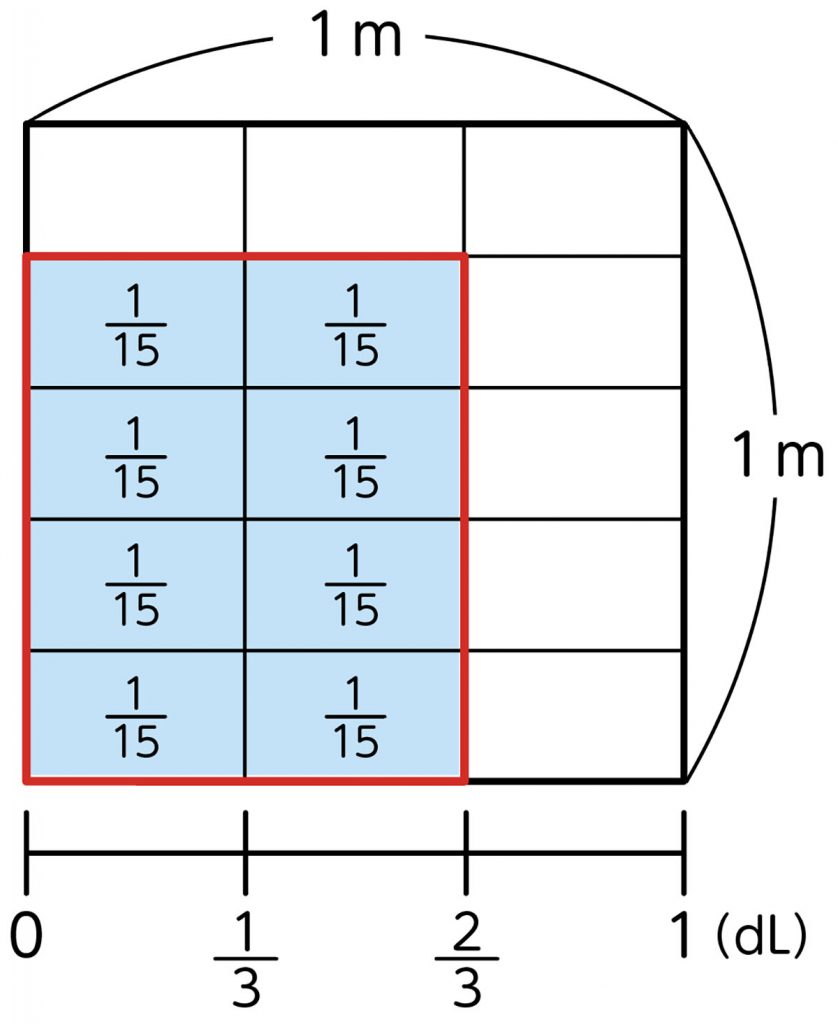
[MATH]\(\frac{4}{5}\)[/MATH]×[MATH]\(\frac{2}{3}\)[/MATH]の図を見ると、１マス分は、[MATH]\(\frac{1}{5}\)[/MATH]×[MATH]\(\frac{1}{3}\)[/MATH]＝[MATH]\(\frac{1}{15}\)[/MATH]。
それが、４×２で８マスだから、[MATH]\(\frac{8}{15}\)[/MATH]㎡。

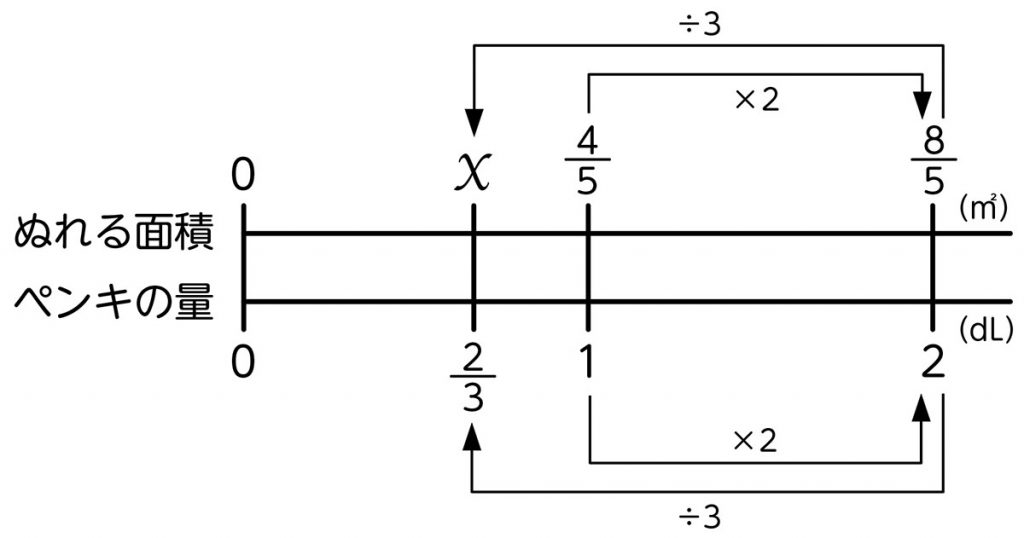
C2　かける数を整数に直して計算する。
[MATH]\(\frac{4}{5}\)[/MATH]×[MATH]\(\frac{2}{3}\)[/MATH]＝[MATH]\(\frac{4}{5}\)[/MATH]×[MATH]\(\frac{2}{3}\)[/MATH]×３÷３＝[MATH]\(\frac{4}{5}\)[/MATH]×２÷３＝[MATH]\(\frac{8}{15}\)[/MATH]