小4算数「直方体・立方体」指導アイデア
執筆／新潟県公立小学校教諭・志田倫明
編集委員／文部科学省教科調査官・笠井健一、新潟県公立小学校校長・遠藤昇
目次
本時のねらい
本時3／12時
立方体の箱を切り開いて広げる活動を通して、面や辺のつながりや重なりを考えることができる。
評価規準
展開図を基に、立方体の面や辺のつながりや重なりについて考えることができる。
問題1
立方体の箱を切り開いたら、次のような形になりました。辺を何本切ったらこの形になるでしょう。
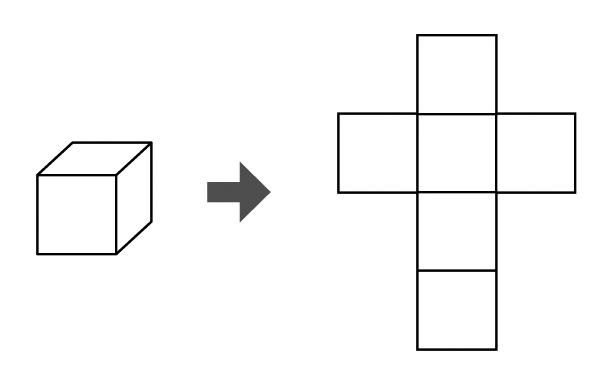
12本切ると切りすぎな気がする。
辺は全部で12本あるから12本でしょ。
12本すべて切ると、面がバラバラになって離れちゃうよね。
面がバラバラになるってどういうこと?
どうして12本ではないのかを説明させることで、辺と辺のつながりを考えることまで、課題を焦点化させる。
例えばここの辺はつながっているから、全部切ったらダメだね。
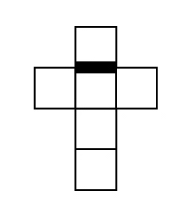
例えば、この辺とこの辺がくっついていたということだから、それを考えればできる。
学習のねらい
辺と辺のつながりを考えながら、切った辺の本数を求めよう。
見通し
立方体と展開図を見ながら考えよう。
構成要素（辺や面など）の位置や大きさは、図形領域の本質的な内容となる弁別に必要な視点です。手元に具体物がなければ立体の概念は育ちません。立方体と展開図を一人一つずつ配付し、考える時間をとりましょう。
自力解決の様子
A つまずいている子
立方体のどこの辺が、展開図のどこの辺と対応しているのか分からない。また展開図を見て、どの辺とどの辺がもともとくっついていたのか分からない。
B 素朴に解いている子
一つずつ順番に分けたり、まとめて分けた後に調節したりして、場面に合った等分の操作ができている。
C ねらい通り解いている子
辺の総数12本から今くっついている辺5本をひいて求める（総数12本の半分のような誤答も含めて、数えないで計算で確かめている）。
学び合いの計画
自力解決に取り組ませた後、2～3人で解決方法を紹介し合うようにします（子供の状況に応じて、話合いを先にします）。つまずいている子供も、辺と辺のつながりに着目して考える状態にすることを、この時間を設定する目的とします。
ノートの例
全体発表とそれぞれの考えの関連付け
何本の辺を切ったと思いますか。どうやって求めましたか?
僕は10本だと思う。だって、展開図のここの辺とここの辺がくっついているから。
離れているけど、この辺はこの辺とくっついているから私は7本だと思う。
展開図のすべての辺が14本。14÷2＝7。だから7本。
14÷2の意味は分かりましたね。12−5という式で求めた人もいました。どのように考えたのでしょう。
まず、辺と辺を対応させながら数えさせます。一人ではなく、辺の位置ごとに複数の子供に説明させ、全員が辺のつながりを考えられるように配慮します。
12や5って何を表しているのかな。
12は立方体の辺の数。5をひくってどういうこと?
5は展開図の面と面がつながっている辺の数だ。
だから12本から５本をひいた残りの7本は切った辺になるのか。確かめよう。
12本あった辺のうち、5本はそのまま切っていないということだね。
学習のまとめ
- 展開図を見て、もともとつながっていた2本の辺をペアにして数えると求めることができる。
- 立方体や展開図の辺の数を基に、計算して求めることができる。
7本の辺を切ったら、本当にこの展開図になるか確かめましょう。
※一人一つ持っている立方体を、全員で一緒に辺を一本ずつ切っていく。別の形の展開図を取り上げ、その展開図が7本の辺を切ってできたことを説明させる。
この展開図も、つながっていた辺のペアが7組ある。だから切った辺は7本だと分かる。
この展開図もつながっている辺が5本ある。立方体の辺の数から5本ひいて12−5で7本切ったと分かる
感想
いろんな種類の展開図ができたから、全部で何種類できるのか調べてみたい。そして、すべて辺を7本切ればできるのか、確かめてみたい。
7本切ったら、全員が立方体を展開できることを確認します。そのうえで、教師が提示した展開図とは異なる展開図ができたことを取り上げます。その展開図で辺を7本切ったことを説明させ、本時の学習内容の習熟を図ります。その後、複数の種類の展開図ができていることを取り上げ、新しい問いを話題にしていきましょう。
『教育技術 小三小四』2021年3月号より
