単位分数を変えながら数直線づくりをし、分数も数であると意識させる【｢系統」を見通し、学年ごとに押さえる！ つまずきなしの「分数」指導法 #4】
前回から、３学年の分数指導について、新潟市立上所小学校の志田倫明先生に具体的な授業場面で説明していただいていますが、今回は簡単な分数の加法、減法の指導について話していただきます。
目次
たし算やひき算は同種同単位のものでなければ計算できない
前回は、３学年の分数指導の知識・技能の中から､（ア）端数部分の扱い（イ）単位分数の幾つ分、を中心に説明していきましたが、今回は（ウ）簡単な分数の加法及び減法の意味を理解し、それらの計算ができることを知ることについて、具体的な授業場面を例に取りながら説明をしていきたいと思います。
ここでは本当に簡単な場合について学習するのですが、実は前回ご説明した授業場面でも、子供たちが45を出すときに、15＋15＋15＋15という式表記を出す場合もあります。そういったものを認めていってよいと思いますが、ここではもう少しまとまりで見た場合を扱っていきます。例えば、15＋25＝35というものがそれです。
２学年の素地指導を除いて、子供たちはこれまでの学習では整数を扱ってきましたから、１つの数値を表すのに使われる数字は１つでした。しかし、分数では分母と分子、２つの数字が使われています。ですから、よく起こる間違いが、15＋25という計算式だけを見て、分母と分母を足し、分子と分子を足して３/10にしてしまうというものです。このような間違いをしてしまう子が必ず出てきます。
｢ではこの式を計算するときに、どう考えたらいいんだろう？」と考えるときに役立つのが、前回の学習で使ったようなdLマスを等分した図です。図を示して、｢15dLはこういう量だったよね、25dLはこういう量だったね。じゃあ、この15と25をたすとどうなるかな？」と問えば、算数が苦手な子供でも色を塗るなどして考えることができますから、35dLと考えることができます（資料１参照）。
【資料１】
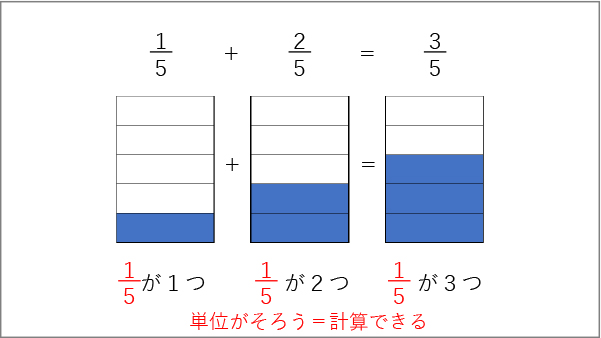
この場面で子供がどのように考えているかというと、つまりは15dLが１つだったものと、15dLが２つだったものを合わせると、15dLが３つになるということで、基になる単位が同じだということです。これは、たし算、ひき算の原理原則です。たし算やひき算は同種同単位のものでなければ計算ができません。過去の学習で、例えば２＋３を計算するときも、１が２個と１が３個だから１が５個と計算したわけです。それが２＋30であれば、１が２個と10が３個なのでたせません。だから、10が３個であれば、１が30個と単位を揃えて計算し、32としていました。このように整数の世界では位を揃えていましたが、単位が揃うからこそ計算ができていたわけです。
ですから、｢310」と言う子供がいたときに、｢そもそも15dLってどういうものだっけ？」｢25dLってどういうものだっけ？」と問いかけ、図に描かせて、単位分数である15が１つ分と２つ分という意味に立ち返って考えさせたり、310との違いを確認したりすることが大切です。そこをしっかり確認すれば、｢15が１つと15が２つあるものをたすと、110が３つになるというのはおかしいよね」ということに気付けるでしょう。
