友達が解決できないときに、説明できるようになることが大事【「高校につながる英・数・国」の授業づくり #39】

前回は、兵庫県・神戸市中学校実践研修数学グループの幹事長を務める、神戸市立高倉中学校の田村洋幸教諭に、授業づくりの考え方について伺いました。今回は、対話を通した学びを大切にしている田村教諭に、3年生の授業についてお話を伺っていきます。

田村洋幸教諭
目次
グループで説明し合って、数学的に深く考えていこうという授業
田村教諭は、今回紹介する3年生の単元「関数 」の章末の授業を行った背景から話し始めます。
「この授業は、私が本校に異動してきてすぐ担任した3年生の授業です。令和4年度だったので、まだコロナ禍の下、マスク着用が義務のとき。異動してきたばかりでしたから、それまでどういう授業をやってきたのか分からない状況ではあったのですが、前任校でも同様の取組をやってきていたので、同じように取り組んだものです。
これは3年の教科書の内容を学び終えた後の章末の授業なので、グループで説明し合って、数学的に深く考えていこうという授業です(資料参照)。
【資料】指導案
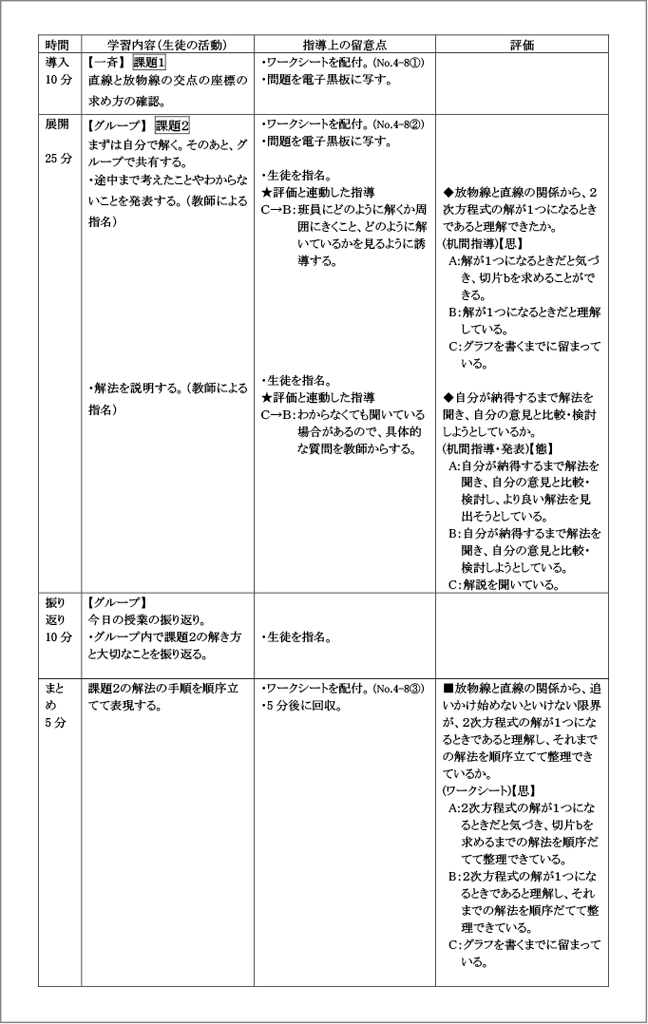
ワークシート
授業の流れ自体は、課題1と課題2を50分通して解くだけという非常にシンプルなものです。課題2が深い問題で、これは1次関数と2次関数の接点を求める学習と考えると、高校の内容に踏み込んだものになってしまいますが、3年生の既習事項を使えば解決できる問題でもあります。
中心となる課題2は、1問だけではありますが、仕掛けがたくさんあって非常に時間がかかるのです。まず、転がっていくボールの位置に関わる放物線のグラフを書いて、『これはこういうことなんだよね』と理解し、グループで共有する。そして、追いかける人のグラフを書いて、『これはこの問題のここを表したグラフだよね』と共有する。そして、『このグラフをこうすると、こういう状況になるよね』、『だから、このグラフのここを求めたらいいんだ』『じゃあ、ここはどうやって求めたらいい?』と考えていくステップが、5段階あるいは6段階くらいあります。
それをその都度、グループで共有したり、グループで分かったことを学級全体で共有したりしながら、理解を深めていきます。そうやって互いに説明し合って、考え方を共有しながら問題解決を図る学習をやっていきました。
この課題1については、すでに学習した知識の問題ですから、10分程度あればできていました。この課題1を使って課題2を解いていくのですが、先に説明したようにステップがたくさんあるため、30分くらいかかりました。
ちなみに課題2では、ボールが坂道を転がっていくため2乗に比例すると見て2次関数で表し、追いかけていくA君は等速運動をしていると見て、1次関数で表したものです。これは最初にも言ったように、2次関数と1次関数の接点の問題と見れば、高校の問題になるのですが、高校の学習でも、中学校の既習を生かしながら解いていくわけですから、できないことではありません。
もっと子供たちにとって分かりやすい考え方で言えば、転がっていくボールを表す放物線と、追いかけるA君を表す1次式の直線が接点をもたなければ、『A君は追い付けない』ということです。それが分かって、1次式の切片を操作して、答えを求めようとしていれば、私は評価Bと判断しました。
これは3年生の2学期の学習ですし、受験に向けて学習している時期でもありますから、私からは余計なことは言わず、子供たちが対話しながら学習している状況を見とっていました。そして、見とった解決過程の中から、ポイントとなるものについて、『今、〇〇さんがこんなことを言っていたよ』と話し、その考え方を板書させて全体に共有するというような形で授業を進めていったのです」

