小６算数「比と比の利用」指導アイデア《等しい比の性質を使い、同じ濃さの乳酸飲料の量を考える》

特集: 文部科学省教科調査官監修｢教科指導のヒントとアイデア｣

2024.11.29

単元の展開

第１時　ご飯の材料の分量の割合について考える。
▼
第２時　ご飯の材料の分量の割合について考え、比を用いた割合の表し方、比の値を知る。
▼　
第３時　棒と影の長さの比の値を調べ、２つの比が等しいことの意味を理解する。
▼　　　《比が等しいことの意味の理解》
第４時　等しい比が複数あることを見付け、２つの比の間に成り立つ性質について考える。
▼　　　《等しい比の間に成り立つ性質》
第５時（本時）等しい比の性質を使い、同じ濃さの乳酸飲料の量を考える。
▼
第６時　等しい比の性質を使って、できるだけ小さい整数の比を見付ける。
▼
第７時　等しい比の性質を利用して、影の長さを基に木の高さを求める。
▼
第８時　72㎝のリボンを使い、比例配分の意味と計算の仕方を考える。
▼
第９時　黄金比・白銀比を知り、身の回りのものの比について考える。

本時のねらい

乳酸飲料について、比の性質や比の値を用いて、同じ濃さかどうかを判断したり、同じ濃さのつくり方を考えたりする。

評価規準

日常の事象における数量の関係に着目し、目的に応じて、図や式を関連付けたり用いたりしながら、比の性質や比の値を用いて、等しい比かどうかを判断したり等しい比をつくったりしている。（思考･判断･表現）

本時の展開

ある乳酸飲料は、原液と水の割合が１と４になっていると、ちょうど飲みやすくなるようにつくられています。次の①と②がちょうど飲みやすいこさかどうかを調べましょう。ちょうど飲みやすいよいこさでない場合は、どうしたらちょうど飲みやすいよいこさになるか考えましょう。
①　原液を120mL、水を480mL混ぜ合わせたとき
②　原液を150mL、水を640mL混ぜ合わせたとき

この問題には①と②がありますが、どちらが調べやすそうですか。

①です。

他のみなさんも①が調べやすいと思いますか。①が調べやすいと思う人は手を挙げてください。

※多数が挙手する。

（つまずいている子に対して） ○○さんは手を挙げにくそうだったけれど、今どんなことを思っていますか。

原液と水の割合が１と４ということは「１：４」ということなので、｢原液100mL、水400mL なら分かりやすいのに」と思っています。

「100：400」ならすぐに分かるけれど、｢120：480」は少しじっくりと調べたいのですね。それでは、みんなでまず、①について考えていくのでよいですか。

※全員が返事をする。

では、まず、①について考えていきましょう。①はちょうどよい濃さですか。

ちょうどよい濃さです。１：４になっているからです。

なぜ、１：４になっているとすぐに分かったのですか。

①は原液と水の割合が120：480になっています。この120と480を比の性質を使って、両方を120で割れば120：480＝（120÷120）：（480÷120）＝１：４で、比が等しくなっていることがすぐに分かるからです。

僕は、120：480の比の値を求めたらすぐに分かりました。120÷480＝[MATH]\(\frac{1}{4}\)[/MATH]で、１：４の比の値の[MATH]\(\frac{1}{4}\)[/MATH]と等しいとすぐに分かるからです。

他のみなさんも、①の「120：480」が「１：４」でちょうどよい濃さということでいいですか。

※ほぼ全員が返事をする。

（つまずいている子に対して）△△さん、２人の説明を聞いて「120：480」が「１：４」だということを納得できていますか。

〈△△〉「120：480」のなかで「100：400」は「１：４」です。残りの「20：80」も「１：４」なので、全体の「120：480」も「１：４」なんだろうなと思っています。

｢480」は「120」の４倍ということを考えたら分かりやすいと思うよ。

480÷120＝４だから、｢120：480」は「１：４」と考えたらどうかな。

△△さんのおかげで、①の「120：480」が「１：４」でちょうどよい濃さということについて、考えが深まりましたね。②の「150：640」についても、同じように調べていけそうですか。

みんなで考えたことを使えば、②も調べることができると思います。

そうだね。できると思います。

②の「150：640」について、どんな見通しをもっていますか。

②は「１：４」にはなっていません。

ひと目見ただけで、②が「１：４」でないことが分かるのですか。

150の４倍は600です。640というのはそれより多いからです。

水が多いということは、薄い味になっているということです。

②の「150：640」が「１：４」でないと考えている人は手を挙げてください。

※全員が手を挙げる。

△△さんも手を挙げていましたね。②について、どう考えていこうと思っていますか。

〈△△〉ちょうどよい味の「150：600」を基にして、味を濃くしてちょうどよい味にすることを考えていこうかなと思っています。

｢１：４」の「150：600」を手がかりに、ちょうどよい味をつくっていこうという見通しをもっているのですね。

それではみんなで、②の「150：640」をちょうどよい味「１：４」にすることについて考えていきましょう。

｢原液150mL、水640mL」をちょうど飲みやすいよい濃さ（１：４）にする方法を考えよう。

見通し

②は薄味なので、味を濃くすればいい。（結果の見通し）

味を濃くするには、原液を加えればいい。（結果の見通し）

味を濃くするには、水を少なくする方法もありそう。（結果の見通し）

比の性質を使って考えたり比の値を求めたりすればできそう。（方法の見通し）

等しい比になるように原液か水の量を増減させたらできそう。（方法の見通し）

自力解決の様子

A　つまずいている子
・薄い味を濃くすることを手がかりに考えようとしている。
原液150：水640について、原液150：水600（150×４）と比べて、薄い味になっていることは分かるが、どうやったらちょうどよい１：４の味に直せるかが分からず、困っている。

Ｂ　素朴に解いている子
・｢１：４＝ 150：600」を手がかりに考えようとしている。
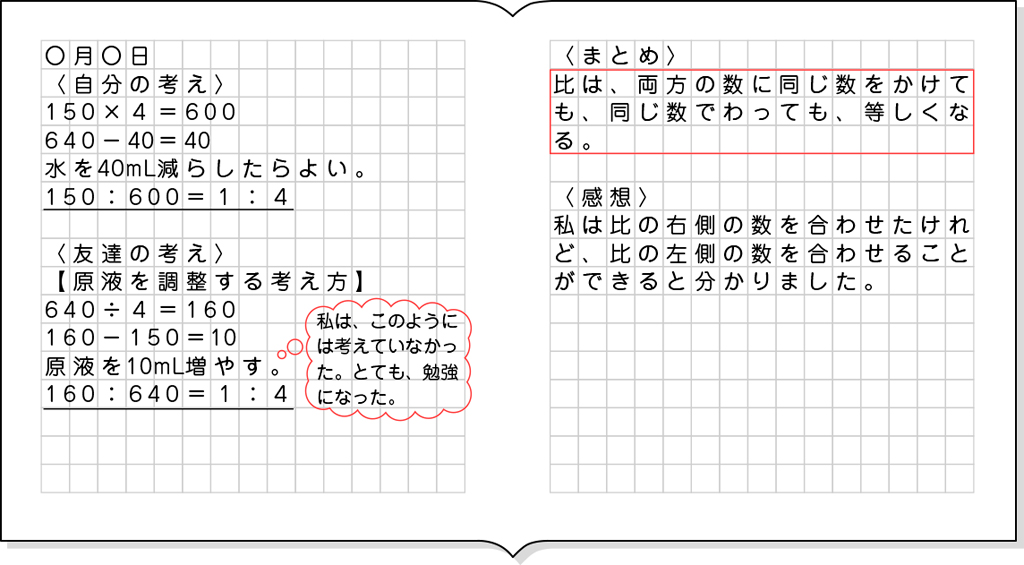
150：640が１：４の味になるように、640を150×４＝600で600にするために、40mLを減らしたらよいと考えている。

Ｃ　ねらい通り解いている子
・｢１：４」に等しい比がいくつもあることから、複数の方法を見通している。
150：640が１：４になるように、以下の２通りの方法を考えている。
⑴ 640を150×４＝600で600になるように、水を40mL減らしたらよいと考えている。
⑵ 150を640÷４＝160で160になるように、原液を10mL加えればよいと考えている。

学び合いの計画

②の問題の場面では、Ｂの子のように考える子供が多いと予想されます。①の問題について考える際に比の値を求めたことで、次の図のような見通しをもっているためです。

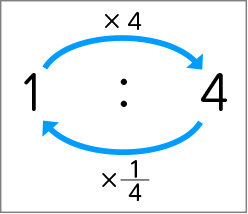
この図のように関係を捉えたとき、計算が苦手な子供は答えが整数になるかどうか分からない640×[MATH]\(\frac{1}{4}\)[/MATH]の計算よりも、150×４の計算を選ぶことでしょう。そうなったとき、Ｃの⑵の原液を加えるという考えが少数派となります。しかし、問題を多面的に捉え、アプローチする力を高めていけるようにするためには、このような解き方と出合い、見方・考え方を広げることは大切です。

そこで、原液を加える考えを全体の場で広げ、問題について多面的に捉える子供を育てるために、全体で話し合う前にグループで話し合う時間を設けるなど、学習形態を工夫するとよいです。工夫の例として以下のようなものが挙げられます。

多くの子供は水を減らす考えで説明し合うので、グループでの話合いでは、｢分からない子供」と「水を減らす方法を説明する子供」というやりとりになります。そういったグループでの話合いのなかに、原液を加えるという逆の発想が出てきたら、話合いは豊かなものになります。

そこで、グループでの話合いを終えた後、全体の話合いの場で「自分と同じ解き方をしていた人はいましたか？」｢自分とは違う解き方をしていた人はいましたか？」と問いかけていくことで、子供たちは水を減らす考え→原液を加える考えと段階的に学びを深めていくことができます。このように、グループで話し合う場を意図的に設け、子供の考えを見とり、全体の場での発問を精選することで、全体で話し合う場を子供どうしが関わり合いながら学び合う場にすることができます。

ノート例

Ａ　つまずいている子

Ｂ　素朴に解いている子

全体発表とそれぞれの考えの関連付け

グループでの話合いで、自分と同じように考えていた友達はいましたか。

いました。

どのような考えですか。

原液の量（150mL）を基にして、水の量を調整していく考えです。まず、比の左側の数の150を基に考えていきます。150倍になっています（150÷１＝150）。次に、比の右側の数も同じく150倍にするので、４×150の計算をします。そうすると、４×150＝600です。原液が150mL、水が600mLのとき、ちょうど飲みやすいよい濃さだということです。でも、比の右側の数は640です。水の量が640mLなので、ちょうど飲みやすいよい濃さの600mLよりは、40mL多いということになります（640－600＝40）。だから、水を40mL減らせばよいということになります

僕も同じように考えました。

私のグループでは、別の考えでやっている人がいました。

どのようなやり方ですか。

水の量（640mL）を基にして、原液の量を調整していく考えです。

みなさん、この考えを聞いてみたくないですか。

ぜひ聞きたいです。（多数）

では、順を追ってていねいに説明してくださいね。

まず、比の右側の数の640を基に考えていきます。640÷4＝160で160倍になっていると見ます。次に、比の左側の数も同じく160倍にするので、１×160の計算をします。そうすると、１×160＝160です。原液が160mL、水が640mLのとき、ちょうど飲みやすいよい濃さだということです。でも、比の左側の数は150です。原液の量が150mLなので、ちょうど飲みやすいよい濃さの160mLよりは、10mL少ないということになります（160－150＝10）。だから、原液を10mL増やせばよいということになります

２つの考えを聞いてみて、どんなことを考えていますか。

基にして考えるのが、水の量なのか、原液の量なのかで、まったく反対の動きになるんだなと思いました。

でも、味の濃さのことを考えてみれば、今は薄いのだから、水を少なくするか、原液を多くするかのどちらかの方法しかないというのは、当たり前のことかもしれないと思います。

そうですね。数字だけを考えるのではなく、それが何を意味しているのかを考えてみることはとても大事なことですね。２つの考えについて、ここが分かりにくかったな、ここをもう一度説明してほしいな、というところはありますか。

〈△△〉何となくは分かったんだけど、数字だけだと考えが頭のなかに入ってきにくいので、図に表したらどうなるのかなと思っています。

図に表すと、見た目で考えることができますね。△△さんの他にも、図で考えてみたい人はどのくらいいますか。手を挙げてください。

※多数が挙手する。

では、こんな図を使って考えてみるのはどうですか。（図を提示する）

分かりやすくてよいです。

私も同じ図を思い浮かべていました。

それでは、みんなでこの図を使って、ここまで考えたことを整理していきましょう。

次の図のように、まず、原液150ｍLを１と見ます。そうすると、原液150ｍLに対して「１：４」の比にするためには、水は150mL（原液）の４倍の600ｍLでないといけません。でも、水は640ｍLになっているから640－600＝40で40ｍL多くなっていることが分かります。だから40ｍL減らせばよいと分かります。