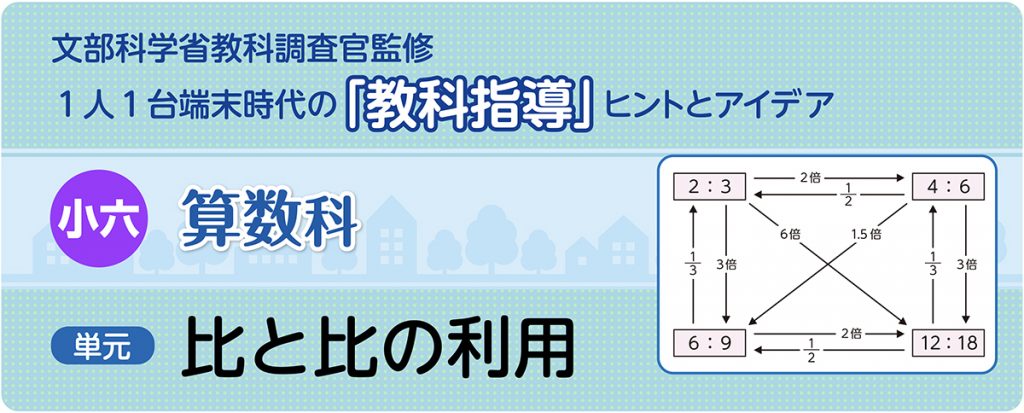
小6算数「比と比の利用」指導アイデア《等しい比の間に成り立つ性質》
執筆/新潟県新潟市立東曽野木小学校教諭・間大也
監修/文部科学省教科調査官・笠井健一、新潟県新潟市立新津第一小学校校長・間嶋哲

目次
単元の展開
第1時 ご飯の材料の分量の割合について考える。
▼
第2時 ご飯の材料の分量の割合について考え、比を用いた割合の表し方、比の値を知る。
▼
第3時 水と白だしの比の値を考え、二つの比が等しいことの意味を理解する。
▼
第4時(本時)等しい比が複数あることを見付け、二つの比の間に成り立つ性質について考える。
▼
第5時 等しい比の性質を使い、同じ濃さの乳酸飲料の量を考える。
▼
第6時 等しい比の性質を使って、できるだけ小さい整数の比を見付ける。
▼
第7時 等しい比の性質を利用して、影の長さを基に木の高さを求める。
▼
第8時 72㎝のリボンを使い、比例配分の意味と計算のしかたを考える。
▼
第9時 黄金比・白銀比を知り、身の回りのものの比について考える。
本時のねらい
神経衰弱ゲームでペアを探す活動を通して、比の値を根拠に等しい比が複数あることに気付き、等しい比が同じ倍の関係にあることを説明する。
評価規準
比の値が等しいことを根拠に等しい比を見つけ出し、等しい比は倍の関係にあることを説明することができる。
本時の展開

神経衰弱ゲームでペアを探そう!
神経衰弱ゲームをしましょう。同じカードをめくって、等しい比が出たらもらえます。
1人1台端末活用アイデア1
ロイロノートを使い、6種類12枚のカードの入ったシートを児童用タブレットに配信します。子供はタブレットを使い、個人で同じカードのペアを見付ける活動を行います。一度に全員へ配信できるため、カードを配る手間を省くことができます。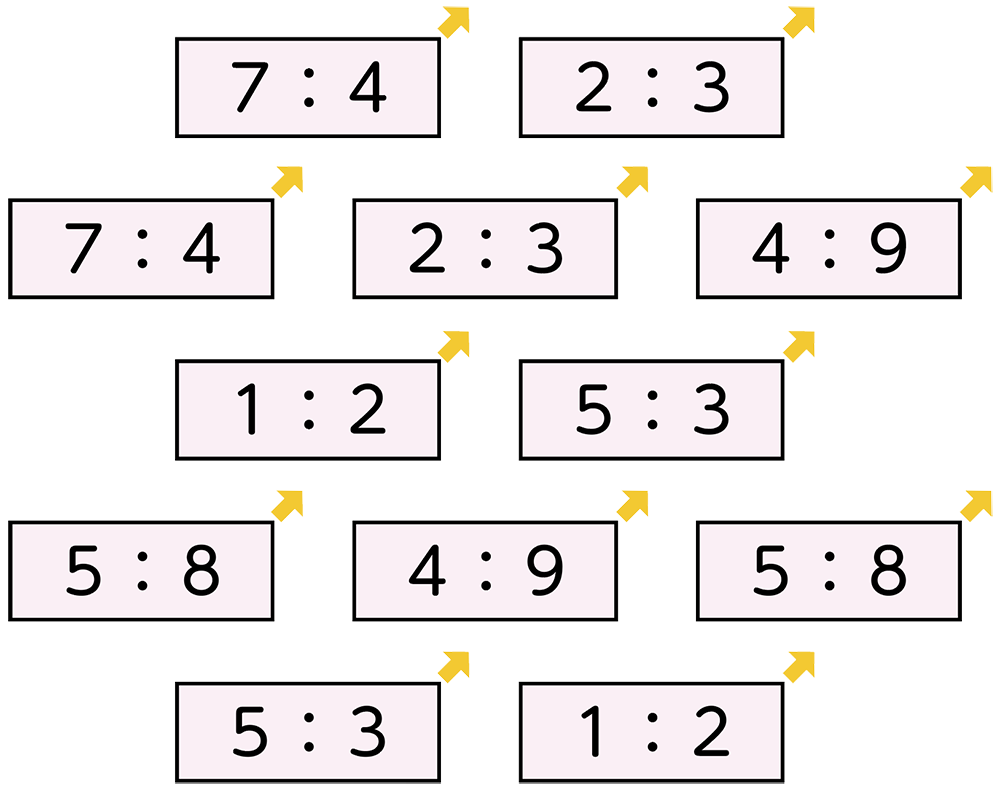
やった、ペアになった。
私は三つのペアを見付けたよ。
次のカードを配ります。次も、ペアを見付けることができますか。
1人1台端末活用アイデア2
ロイロノートを使い、12種類12枚(等しい比)のカードの入ったシートを児童用タブレットに配信します。2回目は、同じカードがないため、子供はめくってもめくっても同じカードが出てこないため、どうしようか悩みます。
同じカードがありません。
同じカードがないなら、どんなカードをペアにしたらよいでしょうか。
同じカードはないけど、等しい比のカードならあります。
えっ、等しい比ならあるの?
等しい比を見付ければ、ペアにできそう。

等しい比を簡単に見付けるにはどうしたらよいだろう。
見通し
等しい比は、比の値が同じだったよね。
比の値が同じペアを見付ければいいんだね。
自力解決の様子
A つまずいている子
等しい比のペアを見付けることができない。
B 図を使って解いている子
比の値を根拠に、等しい比のペアを探すことができる。
C ねらい通り解いている子
等しい比のペアを、比の値を根拠に考えている。さらに、複数の等しい比の関係が○倍になっていることに気付いている。
学び合いの計画
Aの子は、等しい比が同じ割合であることに気付いていません。もしかしたら、1回戦の同じカードにこだわり、同じ数字を探しているのかもしれません。このような子にとっては、等しい比は割合が同じなのですが、数字が同じでないと等しいと感じることができないことが予想されます。
イラスト/横井智美