小６算数「円の面積」指導アイデア《円の求積公式を用いて、複合図形の面積を求める》

特集: 1人1台端末時代の｢教科指導のヒントとアイデア｣

2024.08.15

単元の展開

第１時　方眼を用いて、半径５㎝の円の面積を求める。
▼
第２時　半径10㎝の円を16等分した扇形を敷き詰め、既習の図形に変形させ、面積を求める。
▼　　　《円を分割・変形して面積を求める》
第３時　前時に等積変形させ、面積を求めたそれぞれの式から、求積公式を導き出す。
▼
第４時　正方形と四分円を組み合わせた形の面積を求める。
▼　　　《正方形と四分円を組み合わせた形の面積》
第５時　形の概形を基本的な図形と捉えて、面積を概測する方法を理解する。
▼
第６時（本時）円の求積公式を用いて、複合図形の面積を求める。

本時のねらい

正方形と円が組み合わさった図形について、図形を構成する要素などに着目し、面積の求め方を考える。

評価規準

正方形と円が組み合わさった図形について、図形を構成する要素などに着目し、面積の求め方を見いだしている。（思考・判断・表現）

本時の展開

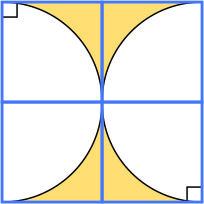
色をぬった部分の面積を求めましょう。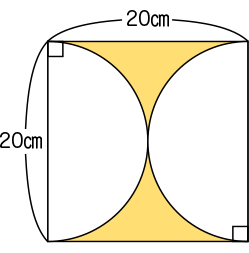

これまで学習してきたことを使って、色を塗った部分の面積を求めましょう。この図形のなかには、面積の求め方の分かる図形がありますか。

正方形があります。

半分の円もあります。

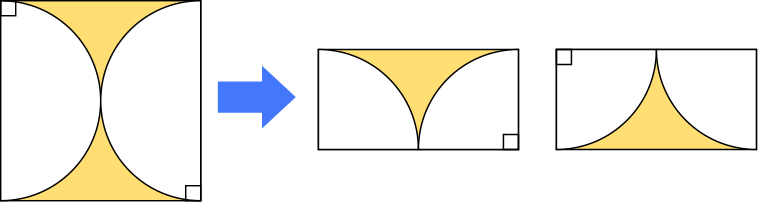
見付けた図形を組み合わせたり取り除いたりして、色を塗った部分の面積の求め方を考えましょう。できるだけ簡単に求められるといいですね。

色を塗った部分の面積を、できるだけ簡単に求める方法を考えよう。

見通し

正方形や半円などの形を組み合わせたり取り除いたりすると、色を塗った部分の面積を求められそうだ。（見通しの予想）

正方形の面積から半円の面積を引くと、色を塗った部分の面積が分かりそうだ。（方法の見通し）

図形を縦に切って左右を入れ替えると、色を塗った部分は正方形から円を引いた部分と同じ面積になるはずだから、簡単な計算で求められそうだ。（方法の見通し）

自力解決の様子

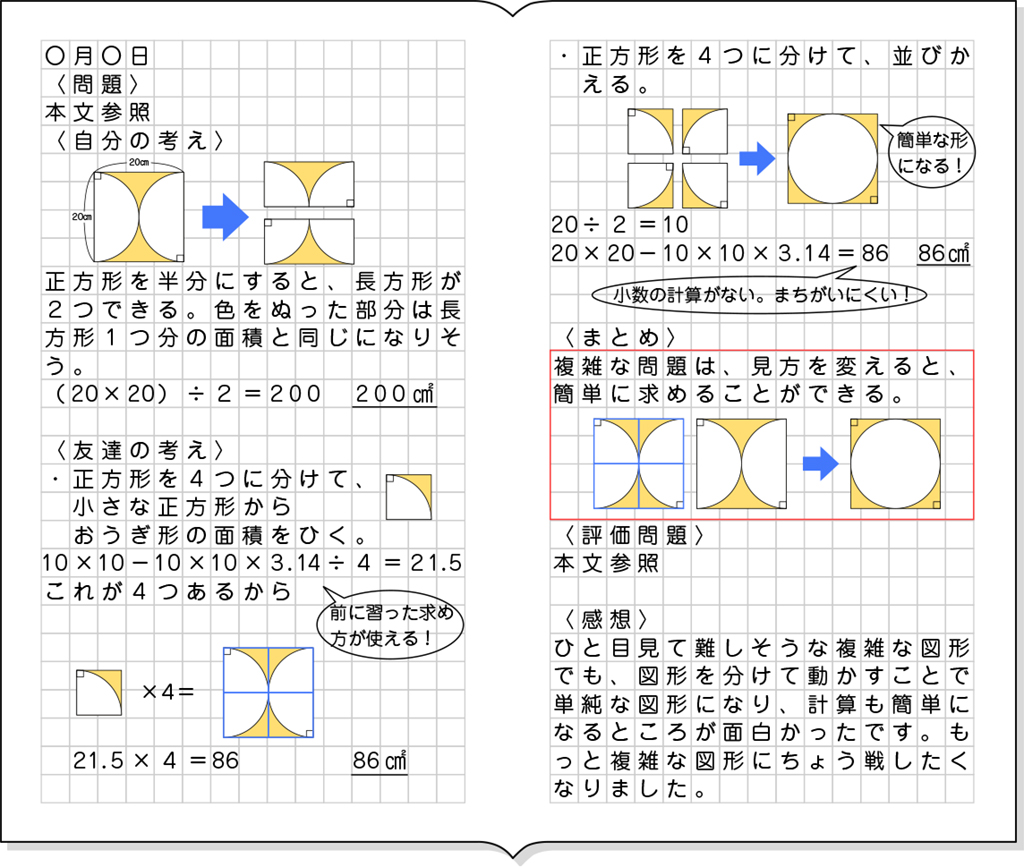
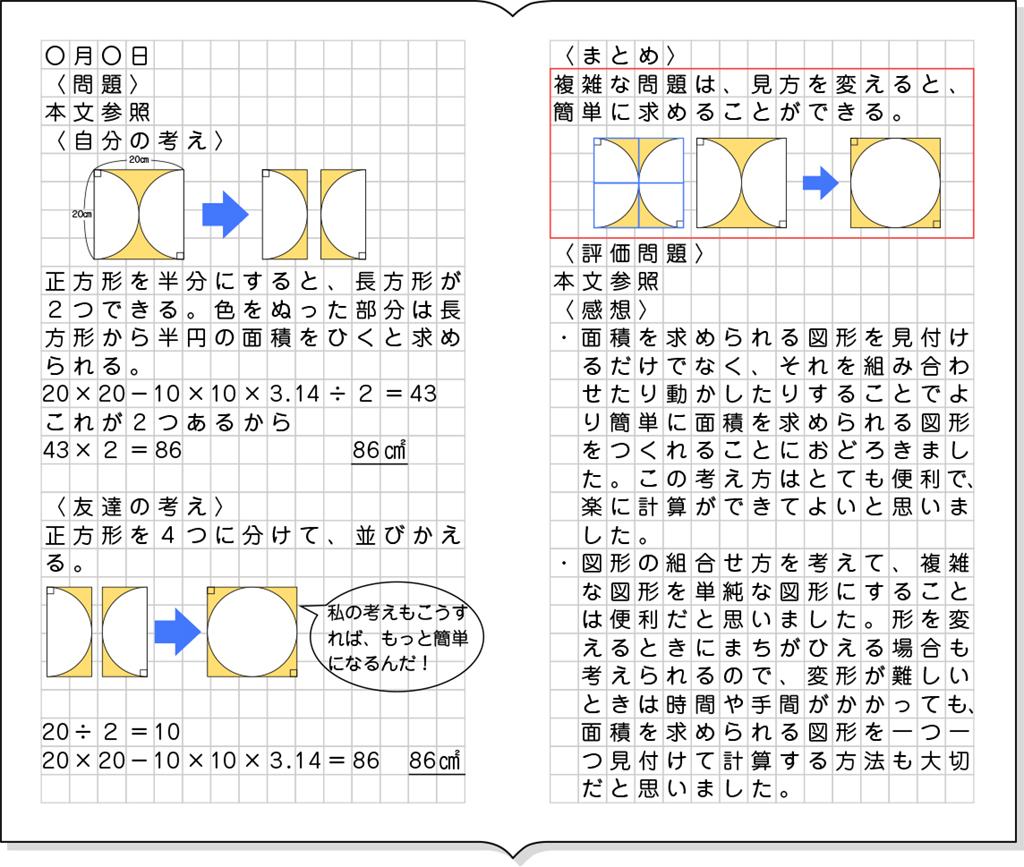
A　つまずいている子
・図形を二分して、それぞれの長方形から差し引く部分の面積が打ち消し合って、正方形の半分の長方形の面積になるのではないかと思い、それを式に表している。

式　（20×20）÷２＝200　　
答え200㎠

Ｂ　素朴に解いている子
・既習内容である[MATH]\(\frac{1}{4}\)[/MATH]の円を基にした考え方で求めている。

式　20÷２＝10
　　10×10－10×10×3.14÷４＝21.5
　　21.5×４＝86　　　　　　
答え86㎠

・正方形のなかに２つの半円があると見て考えている。

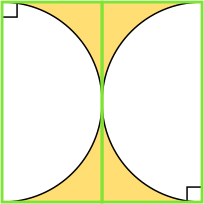
式　20÷２＝10
　　20×10－10×10×3.14÷２＝43
　　43×２＝86　　　　　　　
答え86㎠

Ｃ　ねらい通り解いている子
・正方形のなかに１つの大きな円があると見て考えている。

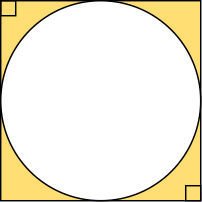
式　20÷２＝10
　　20×20－10×10×3.14＝86
　　答え86㎠

学び合いの計画

本時までに、円を含む比較的簡単な複合図形の面積の求め方を身に付けておくことで、より活発な学び合いの雰囲気が生まれます。しかし、子供のなかには複合図形のなかに隠れた既習の図形を見付けることが苦手な子供もいます。そのような子供も学び合いの場へ参加できるように、以下のような手立てを行いましょう。

●図形が描かれた画用紙を用意し、自由に切ったり、重ねたりする作業を行う。
●デジタル教科書にあるデジタルコンテンツを使用し、視覚的に図形の重なりや図形を移動させる。
●既習の図形を見付けるために、補助線が描かれたワークシートを用意する。　など

学び合う場の設定として、全体発表の前にペアや小グループでの話合いを設けることも考えられます。そこでは、意見の出し合いで終わることがないように留意します。｢グループにいる、解くのが苦手な友達が分かるように説明する」｢考え方の違う友達の意見を聞いた後で、その考え方で自分が解けるのか試す」｢図と式が一致するように、解答に用いた図形を示しながら説明する」など、目的を明確にして話し合うようにしましょう。

全体の話合いの場では、教師が苦手な子供の「？」を取り上げてクラス全員で解決したり、図の切り分けはできるが、式が思い浮かばない子供に寄り添い、立式を導いたり、より簡単に求められる考え方を全員で見付けたりするなど、クラス全員で考えを練り上げていこうとする雰囲気を大切に進めていきましょう。いわゆる分かる子供だけで進めていくことがないように、また、教師がより効率のよい考え方ばかりを認め、粘り強く解いた子供の解法をないがしろにしないようにも注意しましょう。

ノート例

Ａ　つまずいている子

Ｂ　素朴に解いている子

全体発表とそれぞれの考えの関連付け

はじめに、色を塗った面積がどれだけだったか確かめておきましょう。色を塗った面積はどれだけでしたか？

86㎠です。

同じように、86㎠だという人は手を挙げてください。

※多数の子供が挙手。

86㎠とは違う面積の人は、どのくらいいますか。

※数人の子供が挙手。

今手を挙げた人は、どんなふうに考えていますか。

僕は、正方形の半分の200㎠だと思っていたけれど、引いて考える部分を間違っていたのかも知れないと思い始めました。

私も２つに分けて考えたんだけれど、どこからどこを引くのか、わけが分らなくなってきて困っています。

それでは、どのように求めていけばよいのかをみんなで考えていきましょう。自信のあるみなさんは、色を塗った部分の面積をどのように求めましたか。

〈Ｃ１〉僕は、図の縦と横の真ん中に線を引いて、このような図の面積を求めました。

〈Ｃ１〉これは始めの図の[MATH]\(\frac{1}{4}\)[/MATH]の部分だから、この面積を４倍すれば、始めの図の面積になると考えました。この小さい正方形の一辺の長さは、20÷２＝10で10㎝。色の塗った部分は、10×10－10×10×3.14÷４＝21.5で21.5㎠になります。これを４倍すると、21.5×４＝86だから、色を塗った面積は86㎠になると思います。

正方形から扇形の面積を引いて求めたんだね。図形を切って考えると、面積を求めたいところがはっきりと見えてくるね。

〈Ｃ２〉私も線を引いて考えました。でも、Ｃ1さんと違って線は１本しか引きませんでした。

〈Ｃ１〉えっ！？どういうこと。

〈Ｃ２〉私は、このように線を引いて、半円が含まれている長方形を２つつくって考えました。

〈Ｃ１〉なるほど！そういう見方もあったのか。

〈Ｃ２〉求めたい部分の面積は、長方形の２つ分だから長方形の面積を求めて最後に２倍すればよいと考えました。長方形の横の長さは、20÷２＝10だから10㎝。長方形の面積から半円の面積を引いて、20×10－10×10×3.14÷２＝43で43㎠です。求めたい色を塗った部分の面積は、これの２倍だから、43×２＝86で86㎠になります。

同じように線を引く考え方でも、[MATH]\(\frac{1}{4}\)[/MATH]にして考える方法と半分にして考える方法があるのですね。この２つの考え方を聞いて、みなさんはどう思いましたか。

Ｃ１さんの[MATH]\(\frac{1}{4}\)[/MATH]にして考える方法が分かりやすいと思いました。わけは、前の時間に学習した正方形から扇形を引く方法が使えるからです。習ったことをそのまま使えるから、自信をもって解くことができました。

私はＣ２さんの考え方は簡単だなと思いました。２人の式を見てください。Ｃ１さんの式は86㎠を求めるために、10×10－10×10×3.14÷４＝21.5や21.5×４＝86のように小数のかけ算、わり算が出てきます。Ｃ２さんの式は、20×10－10×10×3.14÷２＝43や43×２＝86のように整数のかけ算やわり算しか出てこないので、計算ミスをしにくいのではないかと思いました。

〈Ｃ３〉簡単に考えるのなら、もっといい方法があるよ。

どういう方法ですか。

〈Ｃ３〉僕は、Ｃ１さんやＣ２さんのように基の図形に線を引きました。その後、その線で図形を切り、並べ替えて、正方形のなかに１つの円が入っている図形にしました。

どういうこと。

〈Ｃ３〉切った図形をこのように並べ替えると、どちらの図形も大きな正方形のなかに大きな１つの円がある図形になります。このように形を変えると、大きな円の半径は20÷２＝10で10㎝。正方形から円の面積を引くと、20×20－10×10×3.14＝86で86㎠になります。

〈Ｃ１〉僕の考えた線の引き方で切って並び替えると、大きな円ができあがるなんてびっくりしたよ。

大きな円として考えると、わり算をしなくて済むから、わり算の苦手な私にはありがたいなあ。

図形を切って動かしても求める面積は変わらないから、簡単な図形に直してから計算する方法もいいね。

一見、複雑な図形でも、補助線を引いて切って動かすことで、簡単な図形の組合せに変えることができますね。

先生、私は図形をうまく動かせるか自信がないのだけれど、どうしても動かさないとだめですか。

そんなことはありませんよ。話合いのなかでも出たように、学習したことを使ってていねいに解くことも大切です。自分に合った解き方や考え方を見付けるといいですね。

学習のまとめ

複雑な問題は、見方を変えると、簡単に求めることができる。

評価問題

色をぬった部分の面積を求めましょう。この問題を求めるために、どのような見方をしたらよいか、次の⑴～⑷のなかから選びましょう。

⑴ ４つに分けて考える。
⑵ １つの円と見て考える。
⑶ 正方形から円をひいて考える。
⑷ まず、問題の白い図形の形の面積を求めて考える。

子供に期待する解答の具体例

⑵
ばらばらに求めないで、半径４㎝の１つの円と見ると、簡単な式にできます。
４×４×3.14＝50.24 　　　　　　　　　　　　　
答え　50.24㎠

本時の評価規準を達成した子供の具体の姿

問題を求めるための見方について考え、４等分された円を並び替えて１つの円と見る見方を見いだしている。

感想例

複雑な図形は、面積を求められる図形を探したり、組み合わせてつくったりすることで面積を求められることが分かりました。
基にする図形に補助線を引くことで、面積を求められる図形を見付けることができました。図形をどのように切って動かせば簡単な図形になるのかを考えることが難しかったです。
面積を求められる図形を見付けるだけでなく、それを組み合わせたり動かしたりすることでより簡単に面積を求められる図形をつくれることに驚きました。この考え方はとても便利で、楽に計算ができてよいと思いました。
ひと目見て難しそうな複雑な図形でも、図形を分けて動かすことで単純な図形になり、計算も簡単になるところが面白かったです。もっと複雑な図形に挑戦したくなりました。
求める部分を四角形から円を取り除いた部分と見ることで、簡単に求めることができました。
図形の組合せ方を考えて、複雑な図形を単純な図形にすることは便利だと思いました。しかし、形を変えるときに間違える場合も考えられるので、変形が難しいときは時間や手間がかかっても、面積を求められる図形を一つ一つ見付けて計算する方法も大切だと思いました。
見方を変えることで問題を簡単に見ることができるんだなと思いました。うまい見方を見付けていきたいです。

ワークシート（ダウンロード可）

ダウンロードはこちら＞＞

板書例

学習指導要領

第６学年Ｂ（3）

Ｂ（3）円の面積
（3）平面図形の面積に関わる数学的活動を通して，次の事項を身に付けることができるよう指導する。
　ア　次のような知識及び技能を身に付けること。
　　(ｱ) 　円の面積の計算による求め方について理解すること。
　イ　次のような思考力，判断力，表現力等を身に付けること。
　　(ｱ) 　図形を構成する要素などに着目し，基本図形の面積の求め方を見いだすとともに，その表現を振り返り，簡潔かつ的確な表現に高め，公式として導くこと。
（内容の取扱い）
（3）内容の「Ｂ図形」の（3）のアの(ｱ)については，円周率は3.14を用いるものとする。

｢指導と評価の一体化」のための学習評価に関する参考資料
第６学年Ｂ（3）｢円の面積」