小６算数「場合の数」指導アイデア《表や図を用いて、組み合わせを考える》

特集: 1人1台端末時代の｢教科指導のヒントとアイデア｣

2024.07.30

単元の展開

第１時　表や図を用いて、リレー選手の並び方が何通りあるかを、落ちや重なりなく調べる方法を考える。
▼
第２時　条件がある場合（４枚から３枚を選ぶなど）の並べ方が何通りあるかを考える。
▼
第３時　輪投げして３回投げたときのすべての結果を、◯と×を用いて表す。
▼　　　《重複がある並びの整理の仕方》
第４時　表や図を用いて、アイスクリームの組み合わせを落ちや重なりなく調べる方法を考える。
▼　　　《組み合わせを落ちや重なりなく調べる方法》
第５時（本時）表や図を用いて、５種類のお菓子から２種類、または４種類を選ぶ組み合わせを考える。
▼
第６時　組み合わせの考え方を用いて、身の回りの事象（レストランでのメニューの選び方など）について考える。
▼
第７時　練習問題を解いたり、８チームによるトーナメント戦の総試合数について考えたりする。
▼
第８時　練習問題を解き、学習内容に対する理解を深める。

本時のねらい

（４種類から２種類を選ぶ組み合わせを落ちや重なりなく調べる方法を考え、求めることができるようになった後）

５種類のアイスクリームから４種類を選ぶ組み合わせについて、事象の特徴に着目し、図や表を用いて、落ちや重なりなく調べる方法を順序よく筋道立てて考える。

評価規準

｢５種類から４種類を選ぶ組み合わせ」について、図や表を用いて順序よく筋道立てて考え、｢５種類から１種類を選ばない組み合わせ」と同じであることを、事象の特徴に着目し、筋道立てて考え、説明している。（思考・判断・表現）

本時の展開

食べ放題のアイスクリームコーナーに来ました。
５種類の味（バニラ・チョコ・オレンジ・メロン・ストロベリー）からちがう味の２種類を食べます。選び方は、全部で何通りですか。

※問題１の「食べ放題のアイスクリームコーナーに来ました」まで提示する。

昨日の問題場面と同じだね。選ぶ組み合わせ方が何通りか求めるときは、食べる順番は関係ないから､（バニラ・チョコ）と（チョコ・バニラ）は同じ組み合わせ方になるのだったね。

※問題１をすべて提示する。

２種類選ぶところは昨日の問題と同じだけど、４種類から５種類に増えているところは違うね。

４種類から２種類の選び方は全部で６通り。５種類に増えたから、６通りよりも多くなりそう。

５種類に増えても、表や対戦表に表せば、落ちや重なりなく調べることができるよ。

そうだね。でも、対角線図はどうなるのかな。

４種類から２種類選ぶときは四角形だったね。今日の問題は、５種類から２種類を選ぶのだから、五角形の辺と対角線の数が選び方の通りになるよ。

では、表や対戦表、対角線図に表して、５種類から２種類を選ぶ組み合わせ方が全部で何通りあるか調べてみましょう。

※自力解決する。
※自力解決の際にノートに書いた考え方をICT機器で大きく提示する。

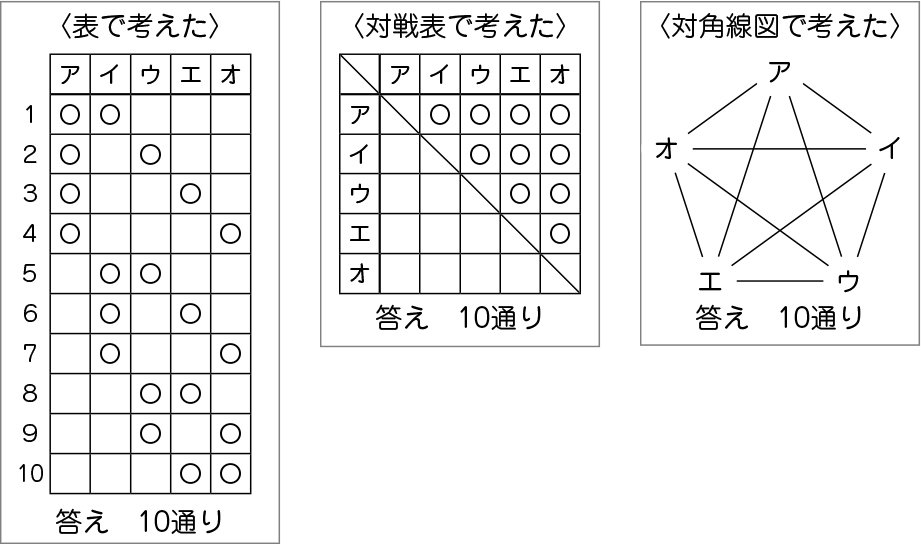
全部で10通りです。

予想通り、６通りよりも多くなったね。

表や対戦表、対角線図、どの方法で調べても10通りになりましたね。では、この場合は何通りになりますか。

※問題２を提示する。

食べ放題のアイスクリームコーナーに来ました。
５種類の味（バニラ・チョコ・オレンジ・メロン・ストロベリー）からちがう味の４種類を食べます。選び方は、全部で何通りですか。

今度は５種類は同じだけど、４種類も選ぶ問題だよ。

４種類も選べるのだから、組み合わせ方は10通りよりも多くなるよね。

そうかなあ。逆じゃないかな。５種類のなかから４種類も選ぶから、パターンは限られてくるよ。だから、10種類よりも少なくなると思うよ。

どっちだろう。表や対戦表、対角線図で調べてみようよ。

今回の「５種類から４種類選ぶ組み合わせ」も、表や対戦表、対角線図で調べることができそうですか。

あっ！　対戦表ではできません。だって、対戦表は、表の縦と横に種類を書いて、交わったところがその組み合わせになります。だから、｢２種類の味を選ぶ組み合わせ」や「対戦する２つのチームを選ぶ組み合わせ」のように、２つを選ぶ組み合わせのときしか使えません。

確かにそうだね。だったら、対角線図でもできないね。

表だったらできそうだよ。順序よく規則に従って調べてみよう。

５種類から２種類を選ぶ方法について調べたことを基にして、５種類から４種類を選ぶ方法が何通りあるのか考えよう。

見通し

２種類選ぶときと同じように、表を用いて順序よく規則に従って調べよう。（方法の見通し）

２種類を選ぶとき（10通り）よりも少なく（多く）なると思う。（結果の大きさの見通しなど）

自力解決の様子

A　つまずいている子
２種類選ぶ組み合わせ方は10通り。その２倍である４種類を選ぶのだから、20通りぐらいではないかと考えている。

Ｂ　素朴に解いている子
表を用いて調べている。まずはＡを固定して考え、順序よく規則に従って調べ、５通りを導き出している。

Ｃ　ねらい通り解いている子
表を用いて調べている。まずはＡを固定して考え、順序よく規則に従って調べ、５通りを導き出している。さらに、その表を観察して、○がついていないところの場合の数も５通りになっていることから、｢５種類の味から４つの違う種類の味を選ぶ」のは、｢５種類の味から１種類の味を選ばない」と考えることもできると気付いている。選ぶ種類が多い場合は、見方を変えることで簡単に調べられると考えている。

学び合いの計画

本時は、｢５種類の味から４つの違う種類の味を選ぶ」場合の数を求める問題場面です。前時や問題１で学習した既習事項と本時の問題２の似ているところや異なるところを明確にすることで、本時の問題場面も表を用いて順序よく規則に従って調べることで求めることができることを見いだしていきます。

さらに、｢５種類の味から４つの違う種類の味を選ぶ」場合の数を求めた後、用いた表をよく観察し、気付いたことを話し合う場を設けることも大切です。そうすることで、｢５種類の味から４つの違う種類の味を選ぶ」のは、｢５種類の味から１種類の味を選ばない」と考えることもできると気付いていきます。そして、選ぶ種類が多い場合は、見方を変えることで簡単に調べられることに気付き、活用する力を高めていきます。

ノート例

Ａ　つまずいている子

Ｂ　素朴に解いている子

全体発表とそれぞれの考えの関連付け

５種類から４種類選ぶ方法は何通りありましたか。

５通りありました。４種類選ぶ場合も、２種類選んだときと同じように表を用いて調べました。（自力解決の際にノートに書いた考え方をICT機器で大きく提示しながら）落ちや重なりが出ないように、まずはアを固定して順序よく◯を書いていきました。

そうそう。だから答えは、５通りになります。２種類選ぶ場合の10通りより少なくなりました。

４種類を選ぶ場合も今までと同じ表で調べられたんだね。

対戦表や対角線図と違って、この表だと、選ぶ種類が２種類以上でも◯の数を増やすことができるから、順序よく整理して調べられるね。

５通りあるということは分かりましたが、この５通りだけで、この他にはもうないということは言わなくてもよいのですか。

それは、そうなんだけど……。

順序よく調べていくと、アを固定して調べると「ア･イ･ウ･エ」｢ア･イ･ウ･オ」｢ア･イ･エ･オ」｢ア･ウ･エ･オ」の４通りありました。次に、イを固定して調べたら、｢イ･ウ･エ･オ」の１通りだけでした。これで調べ尽くしたので、他にはありません。

イの次にウを固定して調べようとしても、｢ウ･エ･オ」の３種類しかないので、４種類を選ぶということはできません。だから、イを固定して調べたら、それで終わるしかないのです。

ウを固定して調べなくてもよいということなんですね。

４種類選ぶときは、ウ・エ・オが固定されることはないから、ウだけでなく、エとオも調べなくてもよいです。

ウもエもオも調べなくてもよいというわけですね。みなさんは、この説明で納得できていますか。

順序よく調べていくと、重なりがなくなるし、抜けていることもなくなるので、これでよいと思います。

今の話を聞いていて、５通りしかないということに自信が出てきました。

私も同じ表を用いて５通りを求めたよ。その後、この表を見て気付いたことがあるんだけど……。

えっ、何？

◯が４つついている場合の数も５通りだけど、◯がついていない場合の数も同じ５通りになっているよ。

確かにそうだね。

この表の◯がついていないところは、何を表しているのですか。

◯は選んだ味を表しているのだから、◯がついていないところは、選ばなかった味を表していると思います。

横に並んだ４つの◯は「５種類の味から４つの違う種類の味を選ぶ」を表し、１か所だけ◯がついていないところは、｢５種類の味から１種類の味を選ばない」を表しているということだね。

そうか。｢５種類の味から４つの違う種類の味を選ぶ」ことを逆の見方をすると、｢５種類の味から１種類の味を選ばない」という意味と同じになるんだね。

５種類から４種類選ぶ場合の数よりも、５種類から１種類選ぶ場合の数のほうが簡単に求められるね。

表を書かなくても、５通りだとすぐに分かるね。

例えば、10種類から１種類選ぶ場合の数だと、10通りになるね。

本当だ！　｢10種類から９種類選ぶ場合の数」と言われるとすごく難しそうだけど、｢10種類から１種類選ぶ」と考えると分かりやすいね。

５と４や10と９のように連続した数ではない場合も簡単になることがあるんじゃないかな。

どういうこと。

｢５種類から３種類選ぶ」は、逆の見方をすると「５種類から２種類選ばない」ことと同じ意味になるでしょ。｢５種類から３種類選ぶ」場合の数を調べるには表を用いるしかないけど、｢５種類から２種類選ぶ」場合の数を調べるときは、表だけではなく対戦表や対角線図を用いることもできるよ。

選ぶ種類の数の大きさによって、そのままの見方で調べたらいいのか、逆の見方で調べたらいいのか判断したらいいね。

いろいろな見方をしてみることが大切なんだね。

学習のまとめ

・バニラ・チョコ・オレンジ・メロン・ストロベリーをア・イ・ウ・エ・オと記号にする。
・アを固定して、順序よく表に表す。
・アの固定が終わったので、次はイを固定する。
・５種類から４種類選ぶので、ウ・エ・オ固定はない。
だから、答えは５通りになる。

評価問題

食べ放題のアイスクリームコーナーに来ました。５種類の味（バニラ・チョコ・オレンジ・メロン・ストロベリー）からちがう味の３種類を食べます。選び方は、全部で何通りですか。

子供に期待する解答の具体例

｢５種類の味から３種類を選ぶ」場合の見方を変えると、｢５種類の味から２種類を選ばない」と同じ意味になる。５種類から２種類選ぶ場合の数は、問題１で求めた通り、10通りある。だから、答えは10通り。

本時の評価規準を達成した子供の具体の姿

｢５種類から３種類を選ぶ組み合わせ」について、｢５種類から２種類を選ばない組み合わせ」と同じであることを、事象の特徴に着目し、筋道立てて考えている。

感想例

「５種類の味から４つの違う種類の味を選ぶ」場合の数は、５通りだということが分かりました。
今回の問題も、場面に着目して表を用いて順序よく規則に従って調べることで、落ちや重なりなく場合の数を求めることができました。また、「５種類の味から４つの違う種類の味を選ぶ」場合の数は、｢５種類の味から１種類の味を選ばない」場合の数と同じだということを考えました。
「５種類の味から１種類の味を選ばない」と考えたほうが、簡単に場合の数を求めることができると思いました。
選ぶ種類の数によって、より簡単に場合の数を求める見方はどちらかを考えてから求めたいです。
５種類から４種類を選ぶのは、５種類から１種類を選ぶことと同じです。このことから、５種類から３種類を選ぶのは、５種類から２種類を選ぶことと同じだと思いました。