子供自身が系統性に気付き、理解していくような授業づくりが大切【｢系統」を見通し、学年ごとに押さえる！つまずきなしの「分数」指導法 #9】

2024.03.14

新しく得た視点でそれまでの学習を捉え直す

前回、異分母分数のたし算を学習する過程で、１学年からのたし算の学習をふり返り、統合していく授業について説明をしました。これは、まさにこの連載のねらいである「６年間の系統を意識した学習」で、それはとても大事なものです。例えば、簡単な分数のたし算は３学年の時点で学習をしています。そのときから、整数も小数も分数も単位が揃っているからたすことができるということを意識できるように指導し、そうしたことへの気付きを価値付けていくことが大事です。そのようにして、子供自身が系統性に気付き、理解していくような授業づくりが大切なのです。

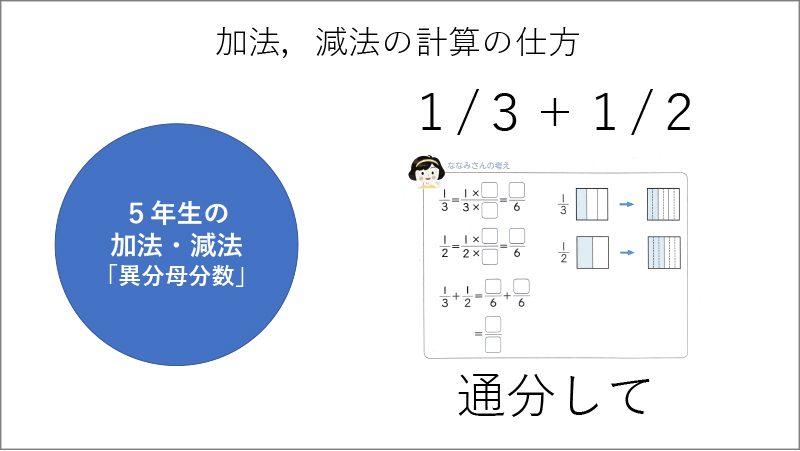
前回の学習に続いてひき算の学習をしたのですが、実はその授業を終えた後、前回「２＋３は何が揃っているの？」と問いを投げてくれた子供が、ざっと次のような話をしてくれました。｢例えば、１年生のとき考えた３－２についてなんですけど、これを１円玉が３つと１円玉が２つと考えると、一緒じゃないですか？　だから単位としているのは『１』で､『１』が３つから『１』が２つを引いているから『１』が１つになります。でも10ー２になると10は10円玉が１つで『10』が１つと考えられるから､『１』が２つとは単位が違って、１ー２はできなくなる。けど、10を『１』が10こと考えると､『１』が10こから『１』が２つを引くと『１』が８つになって計算できます。やっぱり単位を揃えると計算できるということです。これは、通分すると計算できるのと同じことです」と。つまり、加法も減法も単位を揃えるという基本的な考え方は変わらないと統合していったわけです。

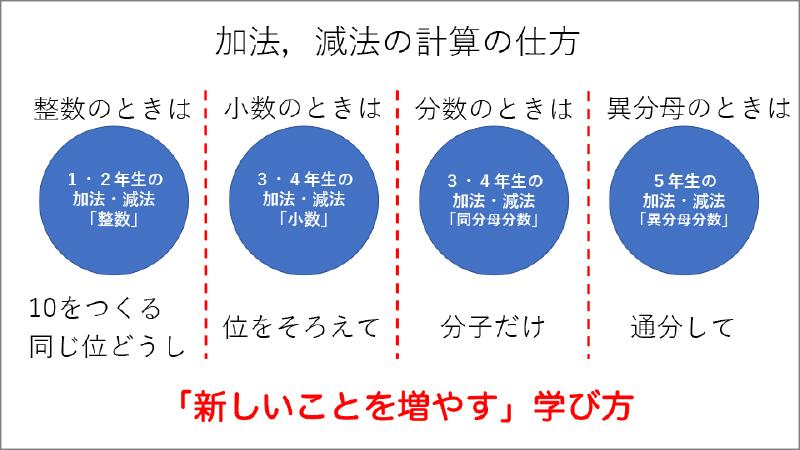
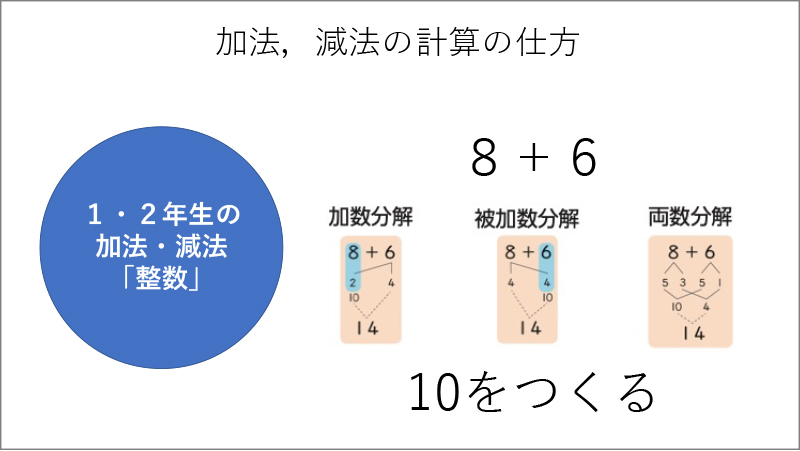
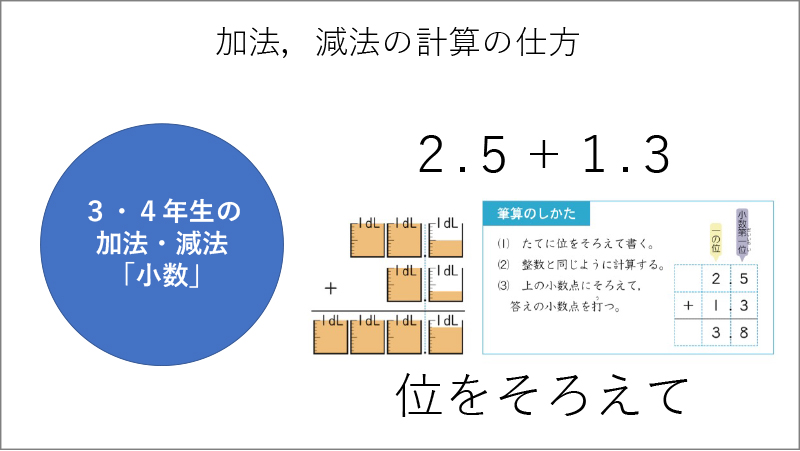
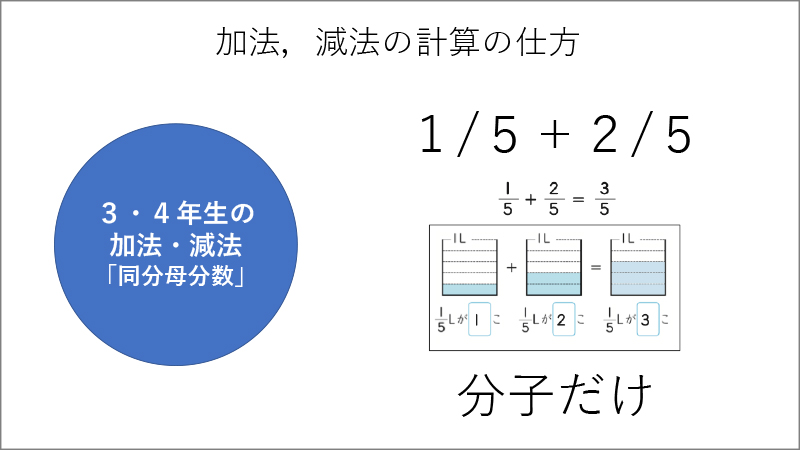
このように子供たちが、新しく得た視点でそれまでの学習を捉え直すことができれば、覚えるべきことはわずかで済みます。もし、このような統合がないまま１学年からの加法、減法の学習を個別バラバラにしていったとしましょう。そうすると、１学年では、10をつくることを学びます（資料１参照）。２学年では、ひっ算を学習し、同じ位同士で計算してまとめていきます（資料２参照）。３学年では、小数が出てきて位をそろえて計算することを学び（資料３参照）、４学年の同分母分数の学習では、分子だけを計算することを学び（資料４参照）、５学年では、通分して計算することを学びます（資料５参照）。

このように計算の方法（手続き）だけを学習すると、それぞれ別個のことを学ぶことになります。これは、子供たちが覚えるべきことをどんどん増やしていく学び方です（資料６参照）。もちろん、この後も学齢が上がるにつれて、どんどん増えていくことになります。そうではなく、先の子供のように通分の学習で単位を揃えるという視点を得たら、その視点で過去の学習をふり返って捉え直してみると、｢このときも、このときも、このときも同じ原理で、単位を揃えて計算していたんだ」ということに気付くわけです（資料７参照）。

算数では、このような原理原則に目を向けていくと学習し、覚えることが少なくなっていくのです。