小6算数「円の面積」指導アイデア(2)
執筆/埼玉県公立小学校教諭・秋山泰孝
編集委員/国立教育政策研究所教育課程調査官・笠井健一、埼玉県公立小学校校長・書上敦志
目次
本時のねらいと評価規準
(本時の位置 4/6 円の面積を求める公式の学習後)
関連記事⇒小6算数「円の面積」指導アイデア(1)
ねらい
円を含む複合図形の面積の求め方を考え、求めることができる。
評価規準
円を含む複合図形の面積の求め方について、既習の求積可能な図形の面積を基に考え、説明することができる。(数学的な考え方)
問題
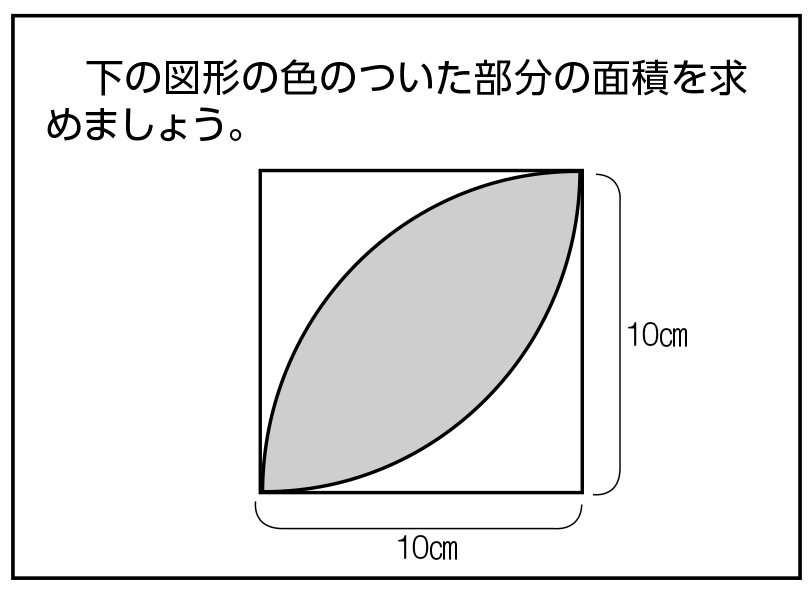
面白い形だね。
ラグビーボールみたいに見えるよ。
では、この形をラグビーボールの形としましょう。これをどうやって描いたと思いますか。
ラグビーボールの外側は正方形だね。
[MATH]\(\frac{1}{4}\)[/MATH]の円を2つ重ねたのだと思います。
これまでに学習した図形が組み合わさってできているね。
面積を求めることはできるかな。
本時の学習のねらい
ラグビーボールの形の面積の求め方を考えよう。
見通し

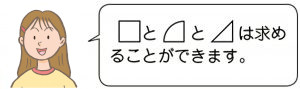
子供の実態に応じて面積を求められる3つの図形と、その面積を求める式を板書し、各自が見通しを持って自力解決に入れるようにします。
直角三角形については、すぐに見いだすことができないことも想定されるため、補助線を引き、子供が気付けるようにします。
自力解決の様子
A つまずいている子
既習の図形を組み合わせてはいるが、求積方法を見いだせない。
B 素朴に解いている子
既習の図形を組み合わせて求めたい図形を作り、求積している。
C ねらい通りに解いている子
面積の求め方を筋道立てて考え、図や式を用いて分かりやすく表現している。
学び合いの計画
学び合いでは、思考した過程や結果などを図や式、言葉を用いて表現し、対話的に伝え合うことで互いの考えを深めたり、自分とは違う考えに気付いたりすることをねらいます。
そのためには、結果のみの発表で終わるのではなく、考えた過程を見せたり、図または式のみを提示し、どのように考えたのかをみんなで読み取ったりする活動を意識的に行うことが大切です。その中で、今までに学習した面積を求められる図形に分けて考えると、複雑な図形でも面積を求めることができることに気付かせていきたいものです。
【本時の子供のノート例】
イラスト/横井智美
『小六教育技術』2018年5月号より
関連記事⇒6年算数 円の面積(1)