小6算数「分数÷分数」 指導アイデア《割る数の分子が1でないときの計算》
執筆/福岡教育大学附属福岡小学校教諭・石橋大輔
監修/文部科学省教科調査官・笠井健一、福岡教育大学教授・清水紀宏

目次
単元計画
第1時 除数の分子が1のときの(分数)÷(分数)の式の意味と、計算の仕方を考える。
▼
第2時(本時)(小数)×(分数)、(分数)×(小数)の計算の仕方を考える。
▼
第3時 除数が仮分数の計算の意味を理解する。
▼
第4時 帯分数で割る計算の仕方を考える。
▼
第5時 帯分数での除法の文章題を、線分図や表を基に解く。
▼
第6時 被除数、除数、商の関係を調べる。
▼
第7時 分数の乗法や除法を適用する問題で、演算決定をし、問題解決することができる。
▼
第8時 既習事項の確かめをする。
本時のねらい
除数の分子が1以外のときの(分数)÷(分数)の計算の仕方を考え、計算の結果や過程をふり返り、公式を導く。
評価規準
除数の分子が1以外のときの(分数)÷(分数)の計算を、既習の計算に帰着して考えることができる。(思考・判断・表現)
本時の展開

□dLのペンキで、かべを[MATH]\(\frac{2}{5}\)[/MATH]㎡ぬることができます。
このペンキ1dLでは、かべを何㎡ぬることができますか。
今日もペンキで壁を塗る場面ですね。前の時間は、□にどんな分数を入れましたか。
[MATH]\(\frac{1}{4}\)[/MATH]や[MATH]\(\frac{1}{3}\)[/MATH]を入れました。
そうでしたね。今日は、この数を入れます。(□に[MATH]\(\frac{3}{4}\)[/MATH]を記入する)

[MATH]\(\frac{3}{4}\)[/MATH]dLのペンキで、かべを[MATH]\(\frac{2}{5}\)[/MATH]㎡ぬることができます。
このペンキ1dLでは、かべを何㎡ぬることができますか。
前の時間の場面との違いが分かりますか。
前の時間はペンキの量が[MATH]\(\frac{1}{4}\)[/MATH]dLだったけれど、今日は[MATH]\(\frac{3}{4}\)[/MATH]dLです。
前の時間はペンキの量の分子が1だったけれど、今日は1ではなく3になっています。
ペンキ1dLで塗れる面積を求める式はどうなりますか。
前の時間と同じように、ペンキの量が割る数になるはずだから、式は「[MATH]\(\frac{2}{5}\)[/MATH]÷[MATH]\(\frac{3}{4}\)[/MATH]」になると思います。
私は言葉の式で考えました。前回の授業で、「塗れる面積」÷「ペンキの量」=「1dLで塗れる面積」だと分かったので、その式に当てはめると、同じように[MATH]\(\frac{2}{5}\)[/MATH]÷[MATH]\(\frac{3}{4}\)[/MATH]になります。
割る数の分数の分子が1でない場合に、分子が1のときの式を使ってよいでしょうか。
数直線を使って考えたらよいと思います。
数直線に数値を書き入れながら考えていきましょう。
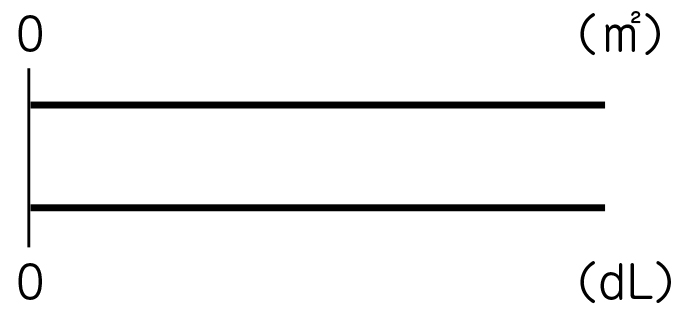
[MATH]\(\frac{3}{4}\)[/MATH]dLで[MATH]\(\frac{2}{5}\)[/MATH]㎡塗れるので、図に数字を書きます。(1dL、[MATH]\(\frac{3}{4}\)[/MATH]dL、[MATH]\(\frac{2}{5}\)[/MATH]㎡を記入する)
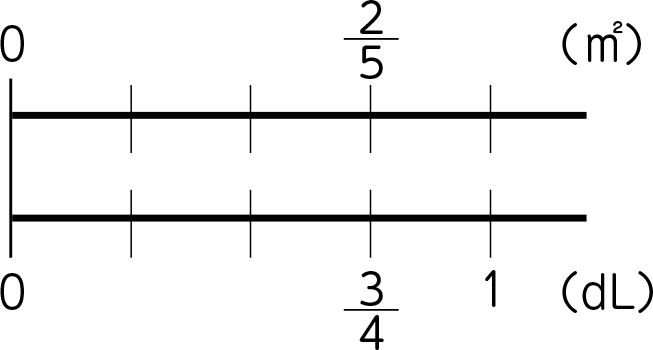
1dLの面積を□にします。(□を記入する)
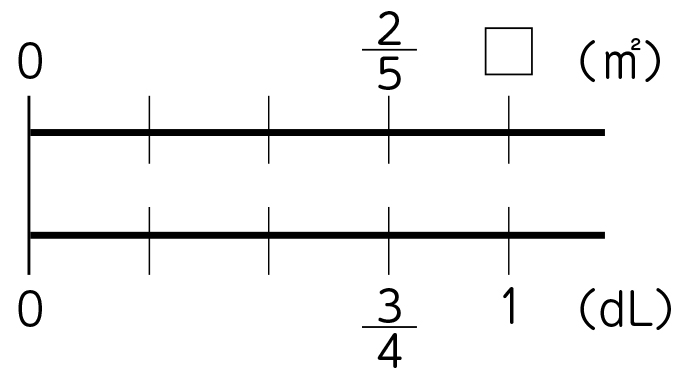
[MATH]\(\frac{3}{4}\)[/MATH]dLと1dLの関係が正確でとても上手に書けていますね。
(矢印や÷[MATH]\(\frac{3}{4}\)[/MATH]を書き入れて)かさでは、[MATH]\(\frac{3}{4}\)[/MATH]÷[MATH]\(\frac{3}{4}\)[/MATH]をすると1になり、かさと面積は比例しているので、面積も÷[MATH]\(\frac{3}{4}\)[/MATH]をします。だから□は、[MATH]\(\frac{2}{5}\)[/MATH]÷[MATH]\(\frac{3}{4}\)[/MATH]になると思います。
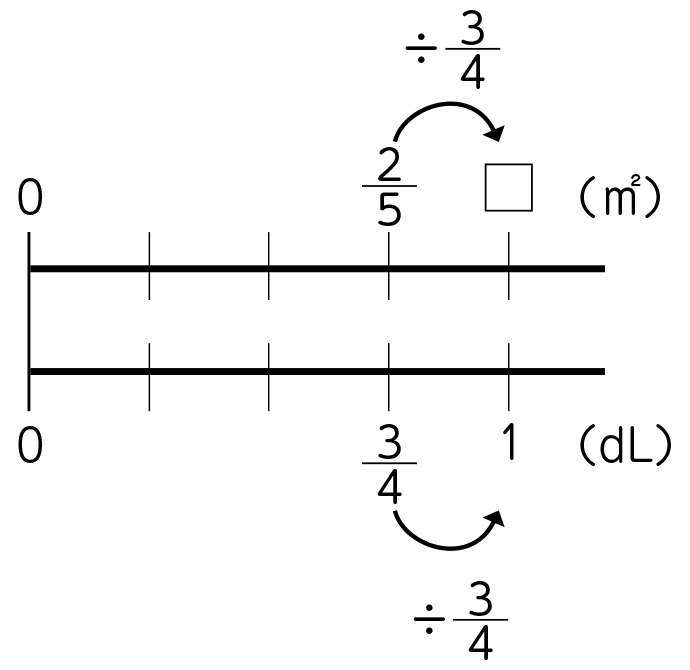
付け加えます。ペンキの量が÷[MATH]\(\frac{3}{4}\)[/MATH]になると、塗れる面積も÷[MATH]\(\frac{3}{4}\)[/MATH]になります。だから、1dLで塗れる面積を求める式は、[MATH]\(\frac{2}{5}\)[/MATH]÷[MATH]\(\frac{3}{4}\)[/MATH]でよいと思います。
なるほど。式はこれでよさそうですね。今日はどんなめあてで学習を進めていきますか。
「割る数の分子が1ではないときの分数のわり算の仕方を考える」がよいと思います。
<めあて>
割る数の分子が1でないときの分数÷分数の計算の仕方について考えよう。
導入では前時の学習(除数の分子が1の除法)をふり返り、前時の学習と本時の学習の違いを明確にします。
前時の学習のノートなどを見れば、式が「[MATH]\(\frac{2}{5}\)[/MATH]÷[MATH]\(\frac{3}{4}\)[/MATH]になるのではないか」と予想できる子供も多いでしょう。このことを予想や言葉の式だけで認めるのではなく、数直線図で確認しておくことが大切です。
また、数直線図でこの場面の2量の関係を正しく捉えることで、□が[MATH]\(\frac{2}{5}\)[/MATH]よりも大きくなりそうだという見通しをもつことにもつながります。
数直線図については、中学年の乗法、除法の学習から系統的に指導していくことで、2量の関係を正しく捉え、演算決定や結果の見積もりに生かせるようにしていきたいものです。
見通し
- 答えは[MATH]\(\frac{2}{5}\)[/MATH]よりも大きくなりそう。
- 図をかいて考える。
- わり算のきまりを使って考える。
自力解決の様子
A 最初はつまずいている子
・今まで学んだ形にして計算したい思いはあるが、どのように工夫すればよいか分からない。
・図がうまくかけない。
B 素朴に解いている子
・まず[MATH]\(\frac{1}{4}\)[/MATH]dLのペンキで塗れる量を求め、それを4倍して答えを求めている。
・除法について成り立つ性質(被除数、除数ともに同じ数を掛けても商は変わらない)を使って答えを求めている。
・図を正しくかき、面積を16等分した後に、[MATH]\(\frac{8}{15}\)[/MATH]㎡が答えであることを導いている。
C ねらい通り解いている子
・答えやその答えを導く過程をふり返り、÷[MATH]\(\frac{3}{4}\)[/MATH]が×[MATH]\(\frac{4}{3}\)[/MATH]であることを導く。
Aの子供には、まず[MATH]\(\frac{1}{4}\)[/MATH]dLで塗れる面積が分かれば、1dLの面積はその4倍で求められることを確認しましょう。
次に前時の学習をふり返り、[MATH]\(\frac{1}{4}\)[/MATH]dLで塗れる面積→1dLで塗れる面積の順に筋道立てて考えていくよう促します。
Bの子供には、答えを求めたことを賞賛しつつ、分数の乗法のような公式を導くことができないか、つまり、答えの求め方を最初の式の数字を使って表せないかどうかを考えさせましょう。
「被除数に除数の逆数を掛ければよい」ことを知っていて機械的に答えを求めて満足している場合にも、そのように計算してよい理由を考えるよう促しましょう。
学び合いの計画
学び合いでは、まず、Bの子の解決方法を取り上げ、答えが[MATH]\(\frac{8}{15}\)[/MATH]㎡であることを確認します。
答えが確認されたら、[MATH]\(\frac{2}{5}\)[/MATH]÷[MATH]\(\frac{3}{4}\)[/MATH]が[MATH]\(\frac{2}{5}\)[/MATH]×[MATH]\(\frac{4}{3}\)[/MATH]であることを導いていきます。
1時間扱いの場合、多くの考えを取り上げることは難しいので、[MATH]\(\frac{1}{4}\)[/MATH]dLのペンキで塗れる量を求め、それを4倍して答えを求める方法をメインで取り上げ、比例の考えを2回使っているということに気付かせ、[MATH]\(\frac{2}{5}\)[/MATH]÷[MATH]\(\frac{3}{4}\)[/MATH]=[MATH]\(\frac{2}{5}\)[/MATH]÷3×4=[MATH]\(\frac{2}{5}\)[/MATH]×[MATH]\(\frac{4}{3}\)[/MATH]であることを数直線図と併せて確認していきます。
面積図による方法についても、答えを求めるだけに使うのではなく、縦の列の面積に着目すれば比例の考えを2回使っていることを説明することができます。
ただし、面積図は数直線よりかくことが難しいので、面積図による方法を授業で扱う場合は、全員の子供がかけるように指導するというよりは、全体交流で面積図を見て、答えや比例の考えを2回使っていることを視覚的に捉えさせればよいでしょう。
除法について成り立つ性質による解法については、①4を掛けて除数を3にする方法、②20を掛けて整数÷整数にする方法、③[MATH]\(\frac{4}{3}\)[/MATH]を掛けて除数を1にする方法があります。
ここでも、①の方法をメインに扱い、ほかの方法は子供の実態や授業の流れに応じて扱うとよいでしょう。
ノート例
B 素朴に解いている子
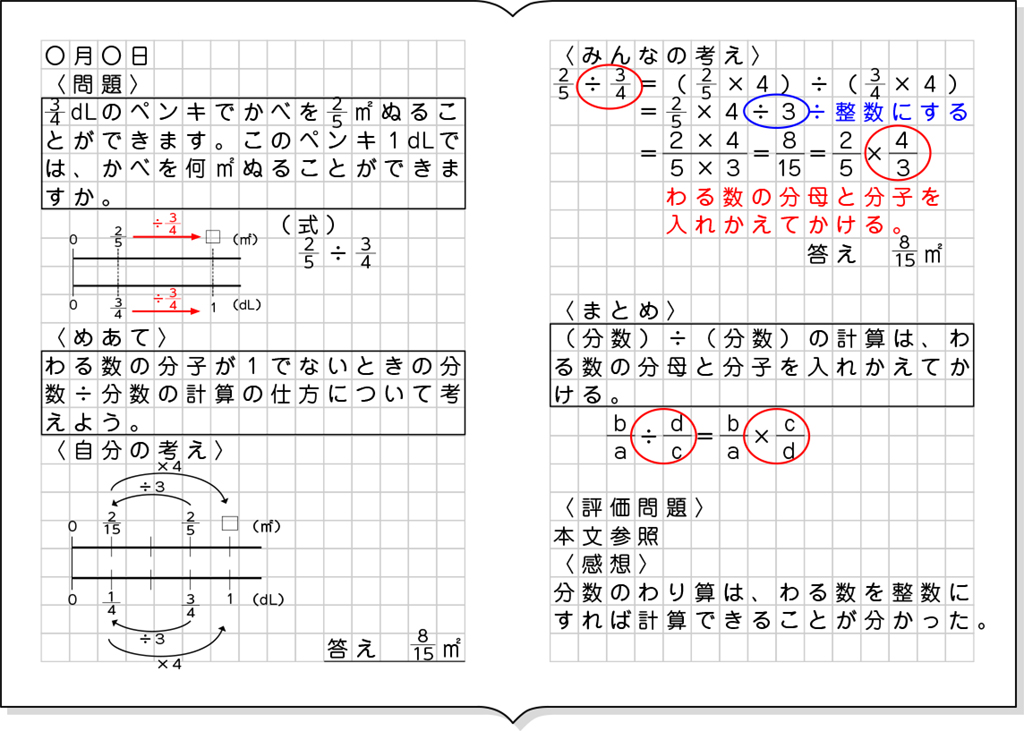
C ねらい通りに解いている子
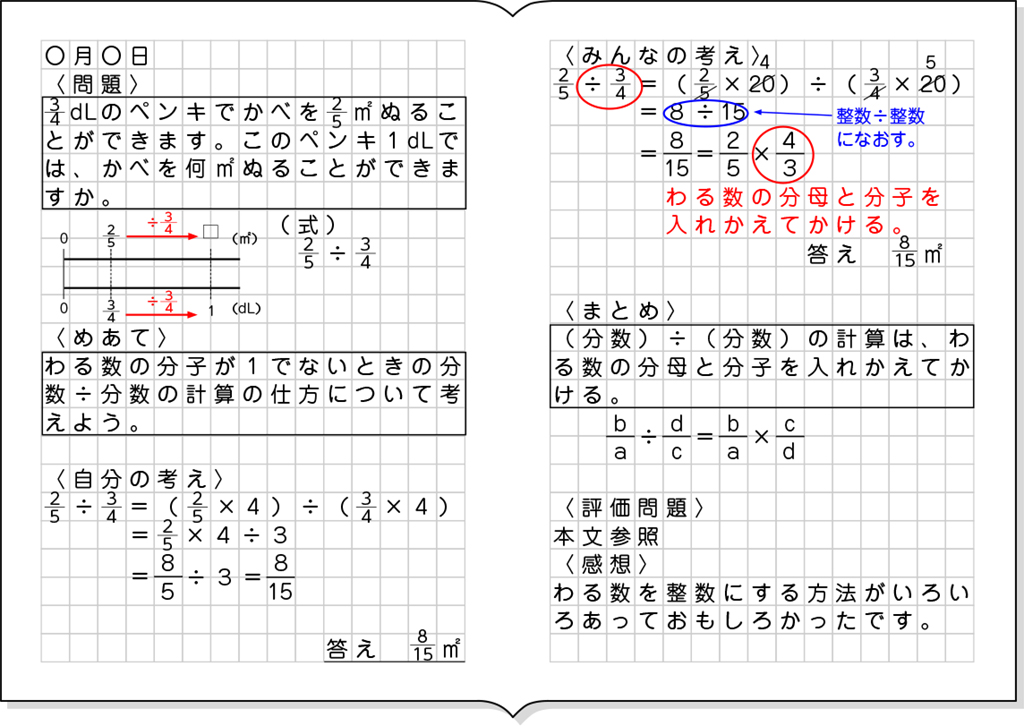
全体発表とそれぞれの考えの関連付け
いろいろな考え方があるようです。まずは◯◯さんに発表してもらいましょう。
イラスト/横井智美

