小6算数「対称な図形」指導アイデア《線対称か?点対称か?》

執筆/福岡教育大学附属福岡小学校教諭・西島大祐
監修/文部科学省教科調査官・笠井健一、福岡教育大学教授・清水紀宏

目次
単元の展開
第1時 折り紙で折られたさまざまな形を線対称の図形・点対称の図形・その他の形に分類する。
▼
第2時 線対称の図形の対称の軸を見付ける。
▼
第3時 線対称の図形の構成要素と図形間の関係に着目し、線対称の図形を定義付ける。
▼
第4時 線対称の図形を作図する。
▼
第5時 点対称の図形を180度回転させ、ぴったり重なることを確かめる。
▼
第6時 点対称の図形の構成要素と図形間の関係に着目し、点対称の図形を定義付ける。
▼
第7時 点対称の図形を作図する。
▼
第8時(本時)特別な多角形の対称性を調べる。
▼
第9時 正多角形の対称性を調べる。
▼
第10時 適用問題
▼
第11・12時 身の回りにある対称な図形を調べる・確かめる。
本時のねらい
対称性という観点から既習の四角形や三角形を見直し、線対称な図形や点対称な図形であるかどうか判断し、その理由を説明することができる。
評価規準
いろいろな三角形について、線対称な図形や点対称な図形であるかどうか判断し、その理由を説明することができる。(思考力・判断力・表現力等)
本時の展開

これまでに学習した、下のような四角形は線対称な図形か点対称な図形かを調べましょう。
また、対称のじくや対称の中心も見付けましょう。
本時では、これまでに学習してきた正方形、長方形、平行四辺形、ひし形、台形の5つの四角形について、対称の観点で調べ、それぞれの図形が線対称な図形や点対称な図形であるかどうかを判断する活動を行います。
まず始めに、本単元において学習してきた線対称や点対称の図形の定義をふり返り、見通しを話し合うことで、めあてにつなぎます。
これまでに学習してきた四角形です。線対称な図形か点対称な図形か、予想してみましょう。
正方形や長方形は線対称の図形だと思います。
正方形は点対称にもなっていると思います。
平行四辺形やひし形も線対称になりそうです。
台形は線対称でも点対称でもなさそうです。
※平行四辺形は線対称ではないが、見通しの段階では多くの予想を引き出し、その後の追究で確かめていくようにする。
いろいろな予想がありますね。ところで、線対称の図形か点対称な図形かを調べるには、どのようなことに気を付けるとよさそうですか。
線対称な図形だと、1本の直線で折ってぴったり重なればよいと思います。
点対称な図形だと、ある点を中心にして180°回転すると、元の図形にぴったり重なればよいと思います。
そうですね。これまでに学習した線対称や点対称のきまりを基にするとよさそうですね。それでは、今日はこれまでに学習したいろいろな四角形を対称の見方で調べて、表にまとめていきましょう(表を配付する)。
めあて
いろいろな四角形について、線対称か点対称か調べよう。
自力解決の様子
A つまずいている子
「平行四辺形が線対称」というように、線対称や点対称の判断に誤った部分もある。
B 素朴に解いている子
5つの四角形について点対称や線対称の判断はできているが、その理由については説明できていなかったり、対称の軸の数が誤っていたりする部分がある。
C ねらい通り解いている子
5つの四角形について点対称や線対称の判断ができ、その理由を操作で確かめたり、ノートに書き込んだりして説明できている。
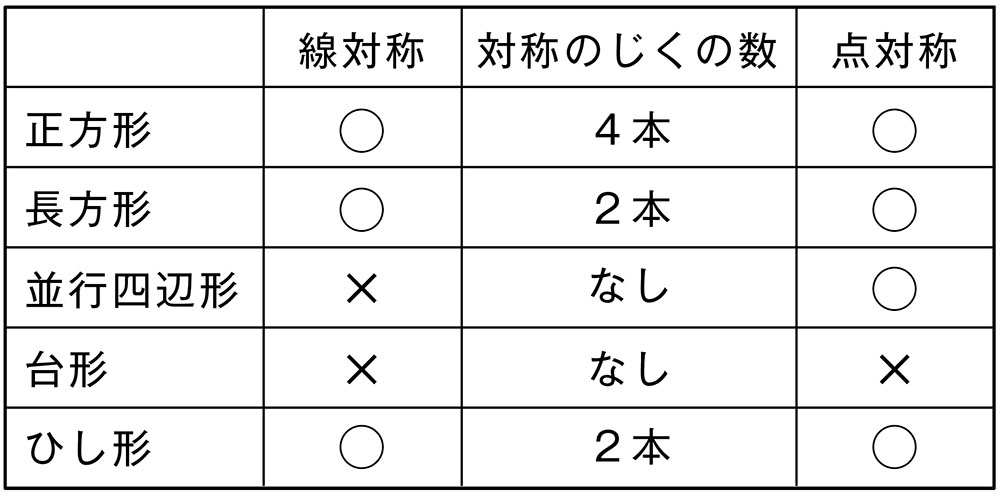
平行四辺形は対称の軸になるところがないので、線対称ではありません。180°回転すると同じ形になるので点対称の図形と言えます。
ノート例
イラスト/横井智美

