小5算数「□と△を使った式」指導アイデア《伴って変わる2つの量の関係を見付けよう》

執筆/福岡県福岡市立片江小学校教諭・村部健太
監修/文部科学省教科調査官・笠井健一、福岡教育大学教授・清水紀宏

目次
単元の展開
第1時(本時)伴って変わる2つの数量の関係に着目し、その関係を□や△を用いた式で表すことができる。
本時のねらい
伴って変わる2つの数量の関係に着目し、その関係を□や△を用いた式で表すことができる。
評価規準
正三角形の個数と棒の総数という2つの数量の関係に着目し、それらの関係を見いだし、□や△を用いた式で表すことができる。(思考力・判断力・表現力等)
本時の展開
本時は、伴って変わる2つの数量の関係に着目し、表や式、図を用いて、それらの関係を一般的に通用する□や△を用いた式で表現することをねらいます。
本時で扱う素材は比例ではないこともあり、□と△の関係式をいきなり問うと子供にとってはハードルが高いかもしれません。
そこで、最初は正方形の数が小さい場面を式に表し、正方形の数が変わっても同じ形の式に表すことができることから、帰納的に考え、□と△の関係式へとつなげていきます。
以上の意図から、問題場面の正方形の数を□にしておき、数値を色々と入れながら授業を展開します。

長さの等しいぼうで、下のように正方形をつくり、横にならべていきます。
正方形を□個つくるとき、ぼうは何本いりますか。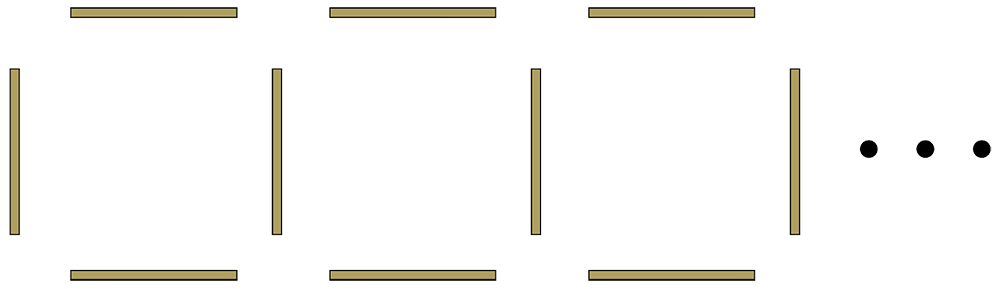
まず、正方形が3個の場合を考えます。棒でこの図をつくっていきます……。できましたね。さて、この問題で尋ねられていることは何ですか。
正方形が3個のときの棒の数を求めることです。
そうですね。何本必要ですか。
(数えるなどして)10本です。
次は□を8個にします。すぐに求められそうですか。
並べたらできます。
このまま正方形が8個できるまで並べていきますか。
並べるのは面倒です。もっと簡単に解ける方法があると思います。
どのように考えていきましょうか。似たような算数の学習を覚えていませんか。
「変わり方」を表で調べたことがあります。
「比例」でも変わり方を表で調べました。式もつくりました。
変わり方や比例では伴って変わる2つの量があります。この問題で変わる量は見付かりますか。
「正方形の数」と「棒の数」です。
「正方形の数」が1個増えると、「棒の数」が何本増えるのか、きまりを見付ければよいと思います。
なるほど。では、今日のめあてを立てましょう。

「正方形の数」と「棒の数」の関係に注目して、棒の数の求め方を考えよう。
先ほど、「『正方形の数』が1個増えると、『棒の数』が何本増えるのか、きまりを見付ければよい」という意見が出ましたが、「正方形の数」と「棒の数」の関係をどのようにして見付けますか。
表をかけばよいと思います。
正方形の図で考えれば、「正方形の数」と「棒の数」の関係が分かると思います。
見通し
- 表をつくる。
- 図で考える。
それでは、自分の考え方で、関係を調べて答えを求めてみましょう。
自力解決の様子
A つまずいている子
- 正方形は4本でできる。正方形8個分と考え、32本とする。
- 増分のまとまりの3本を見付けることができず、どのように解いてよいのか分からない。
Aの子供には、正方形が1個の場合、2個の場合、3個の場合を確認し、答えが(正方形の数)×4でないことに気付かせたり、正方形が1個増えると棒がいくつ増えるかを考えさせたりましょう。
B 素朴に解いている子
- 8個の場合を書いて、数えて本数を求めている。
- 表を書いて、正方形が8個のときの棒の本数を求めている。
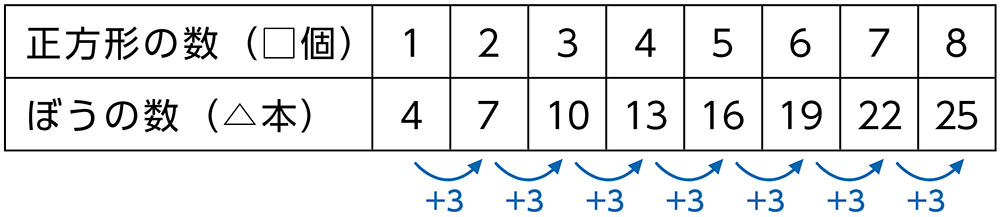
- 正方形が1個増えると棒が3本増えていることに気付いているが、3本多く足している。
4+3×8=28 答え 28本
C ねらい通り解いている子
- 正方形8個とするために、左の正方形に「コの字」を8個より1少ない7個加えればよいことを理解できている。

4+3×7=25 答え 25本
正方形の数8に合わせて、8を7-1と表現すると次の表現になる。
4+3×(8-1)=25 答え 25本
- 左端の1本に「コの字」を3本ずつ増やすことを図で表し、式で表現することができている。

1+3×8=25 答え 25本
学び合いの計画
自力解決の段階で、1人1台端末を活用して、自他の解決方法を共有できるようにし、互いの解決方法を見合うことができるようにしておきます。
イラスト/横井智美