小6算数「比と比の値」指導アイデア
執筆/埼玉県公立小学校教諭・清水武蔵
編集委員/国立教育政策研究所教育課程調査官・笠井健一、埼玉県公立小学校校長・書上敦志
目次
本時のねらいと評価規準
(本時の位置 7/9)
ねらい
比と前項(後項)の値から後項(前項)の値を求めることができる。
評価規準
比の性質や図を用いて比の一方の値を求める方法を考え、説明している。(数学的な考え方)
問題
ケーキを作るのに、砂糖と小麦粉の重さの比が5:7になるように混ぜます。
小麦粉を140g使う時、砂糖は何g必要ですか。
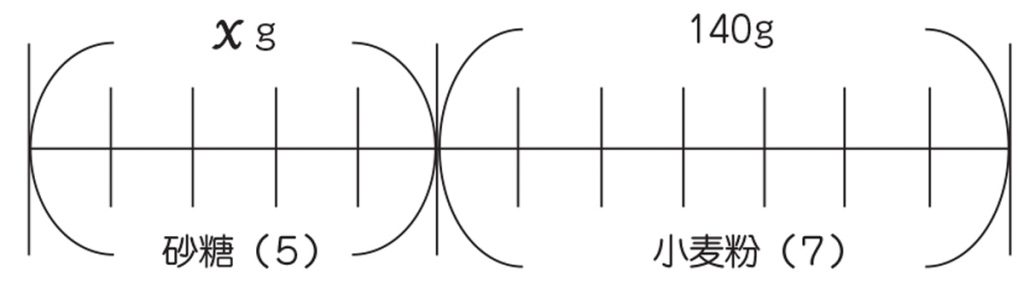
今回の問題は、今までとどんなところが違いますか。
今までは、比や比の値を求めていたけれど、今回は比が分かっています。
問題を分かりやすく整理してみましょう。どのように整理したら分かりやすいですか。
図にしてみれば分かりやすくなります。(線分図を描く)
この問題では、どの部分を求めればよいのですか。
砂糖の量を求めます。
本時の学習のねらい
比の一方の量が分かっている時の、もう一方の量の求め方を考えよう。
見通し
まず、線分図を活用して問題を整理し、どの部分を求めるかを全体で確認します。今回は、比が分かっているので、どの既習(比の値や等しい比の性質)を活用して求めることができるのかを、線分図を基に考えていくことが大切です。
また、解決方法も一つではないので、解決できた子供には、他にも解決方法がないかを考えるように促します。授業の導入で、今までの比の既習を確認しておくとよいでしょう。線分図については、日頃の学習で活用していくことが大切です。
自力解決の様子
A つまずいている子
正しく既習を活用できていない。
砂糖と小麦粉の重さ の比は5:7で、砂糖の量を求めたいから、5を基にして、
140 × [MATH]\(\frac{7}{5}\)[/MATH] = 196
B 素朴に解いている子
比の値や等しい比の性質を活用して、答えを求めることができる。
C ねらい通りに解いている子
等しい比や比の値などの既習を根拠として、考え方の説明をすることができる。
〈例〉等しい比の性質で考えると、砂糖と小麦粉の比は、
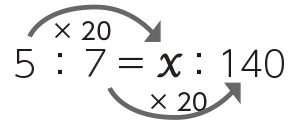
となります。
7に20をかけると140になることから、
5にも20をかけます。
x =5× 20 = 100
既習をしっかりと理解して活用できれば、Cのように説明することができます。しかし、Aのように砂糖を基にして計算し、立式を間違ってしまったり、比の値は比を分数に表せばよいと思っていたりする子供も少なからずいます。そこで、BやCの考えを紹介するだけでなく、なぜ、[MATH]\(\frac{5}{7}\)[/MATH] にする必要があるのか、なぜ5:7= x:140 と表すことができるのかなどの発問をし、子供が線分図と関連付けて説明することが大切です。
ノート例
イラスト/横井智美
『小六教育技術』2018年9月号より






