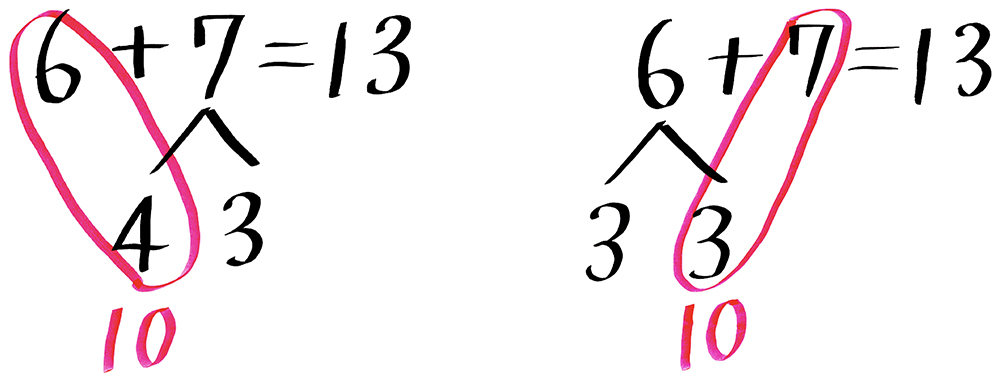１年生「くりあがりのあるたし算」「たし算ひき算」【「算数つまずき防止」ここがポイント！#２】

算数は一つつまずくとその後の学習が進みにくくなる教科ですが、どのような授業づくりをすれば、つまずきを防止できるのでしょうか。今回は１年生「くりあがりのあるたし算」「たし算ひき算」の内容を弘前大学教育学部附属小学校・尾崎珠巳教諭に伺いました。

弘前大学教育学部附属小学校・尾崎珠巳教諭

　　　監修／弘前大学教授・中野博之

式と図と具体物を行き来し、抽象思考への入り口を築く

やはり、１年生の学習で子供たちが最もつまずきやすく定着が難しいのは、「くりあがりのあるたし算」だと思います。

実際に授業をしてみると、多くの子供が答えを求めることはできるようになるため、つい「理解できているな」と思われがちです。ただし、答えを求められる子供たちのなかには、２年生になった時点でも、まだ指を使わないと計算できない子供がいたりします。指を使わないと考えられないということは、10の塊をつくることが本質的に理解できていないのだと思います。そうではなく、10の塊をつくって考える操作が頭の中でできる（＝念頭操作できる、抽象思考ができる）ようにすることが必要だと思います。

では、そのような本質的な理解ができて、念頭操作ができるようにするためにはどうすればよいかということですが、まず苦手な子には少し前の学習に戻って、それを基に考えさせるということが大切だと思います。加えて、式と（分解の）図と具体物を行き来して考えるような学習と板書の整理が必要です。

例えば、私の学校では東京書籍の教科書を使っていますが、単元の最後のほうに、６＋７の学習があります。この計算は、加数７と被加数６のどちらを分解してもよいということになるのですが、ここで少し困り、指を使って計算しようとする子が出てきたりします。

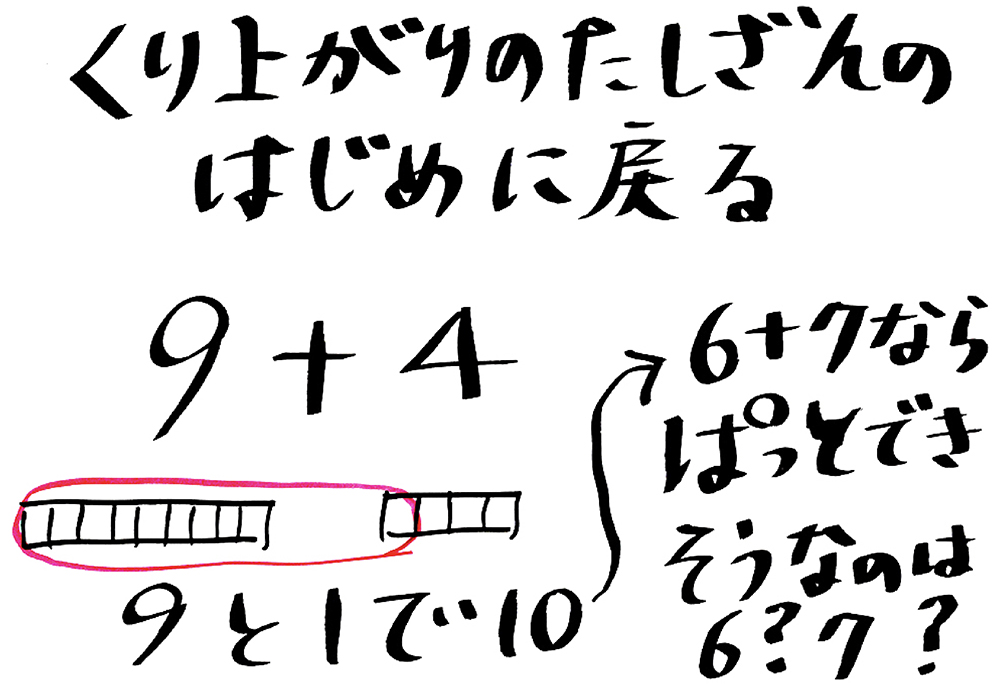
そこで、教科書の前のほうで学習をしている、９＋４という学習に戻り、「あのときはどう計算したかな」と投げかけます。すると子供たちは、「４を１と３に分けて、９と１で10の塊をつくり…」と、加数を分解して10の塊をつくることが簡単にイメージできるのです（資料１参照）。

６＋７では、９＋４と同様に加数の７を４と３に分解してもよいし、今度は被加数の６を３と３に分けてもよいわけですが（資料２参照）、先の９＋４のように「４を分解するとすぐに10の塊がイメージできる」とならない子供に対しては、ブロックのような具体物を使った操作も机の上でさせていくことが必要です。そうした式と図と具体物については、その関係が分かりやすく見えるような板書に整理をしていくことで、念頭操作につなげていくようにしていきます。

そうは言っても、子供たちの日常経験の中では、指を折って数えたりするほうが分かりやすいですし、それも間違いではありません。ただし学齢が上がっていったときには、具体物操作ではなく、抽象的な思考で考えていかないと高度になる内容について考えていくにも、それを友達に説明するにも難しくなってしまいます。ですから、１年生の間に式と図と具体物を行き来しながら考え、説明していくことで、具体物操作から抽象的思考へと移行していくための経験をしていくことが必要なのだと思います。

単なる訓練でなく、子供にとって意味のある学習で定着を図る

１年生の学習では、「くりあがりのあるたし算」の学習過程で、10までの数の分解（と合成）がスムーズにできるようになっておかないと、この後に学習する「くりさがりのあるひき算」で、さらに難しさを感じるようになってしまいます。そのために、６年間の学習の入り口で「算数っておもしろくないな」と思ってしまう子も出てくるでしょう。だからこそ、このときに数の分解（と合成）をしっかり練習しておくことが必要です。

しかし「５は？」と問い、「２と３」「１と４」と答えさせるとか、プリントでただいろんな数を分解する訓練をするというように、子供たちにとって意味のない練習をするのではおもしろくありません。そうではなく、子供たちにとって分解する必然性が感じられる、楽しいゲームのようなものを通して取り組ませていくことが必要だと思います。

おそらく多くの学校で、ブロックやおはじきなどを持たせていると思いますが、それを活用していくわけです。例えば先のような５の分解ならば、ペアの片方の子が最初に５個のおはじきを持っていて、それを左右の手に何個ずつか分けて持ち、左右の手に何個ずつあるかをもう一人の子に当てさせるゲームを行うのです。そこで「３と２」と答えたら、「ざんね～ん。１と４でした」というように楽しみながら、数の分解を身に付けていくわけです。そうすることで、「じゃあ、次はゲームに勝てるように５は何と何に分けられるのか、全部（のパターンを）言えるようになっておかないとな」と子供自身が考え、習熟していくようにすることが大切だと思います。

あるいは、サイコロを振って数を作るようなゲームもあります。ペアの二人で７を作ろうとなると、一人の人が１を出したら、次は６を出さないといけないなと考えて、もう一人の子がサイコロを振るわけです。そのようにして、数の分解や合成が自然にできるようにしていくわけです。

※

このほかに東京書籍の年度末には、「たし算とひき算」という単元があり、文章問題で「Aさんの前には、□人、Ａさんの後ろには□人います。子供は全員で何人いますか」という問題があります。この問題も、子供たちが間違えやすいところで、文章を図に表して式とつなげて考えていかないと正しく考えることが難しい問題です。

実は１年生の最初、５～６月頃の学習に「なんばんめ」という順序数に関する学習があるのですが、それがこの学年末の学習にもつながっているのです。そのように、単元のつながりや系統性いうものを俯瞰しておいたうえで日々の授業を進めると、事前の学習で子供たちへの意識付けの仕方も変わり、より学習が進みやすくなるだろうと思います。

【「算数つまずき防止」ここがポイント！#３】はこちらです。

取材／矢ノ浦勝之