小2算数「かけ算(1)」指導アイデア(1/22時)《乗法が用いられる場合と乗法の意味の理解》

執筆/東京都豊島区立高南小学校教諭・河内麻衣子
監修/文部科学省教科調査官・笠井健一、東京都目黒区立八雲小学校校長・長谷豊

目次
単元の展開
(1)かけ算の意味
第1時(本時)・第2時 「1つ分の数」「いくつ分」を捉え、「1つ分の数」と「いくつ分」の関係の場合に乗法が用いられることを知り、乗法の意味を理解する。
▼
第3時・第4時 乗法の場面を式やおはじきや図で表したり説明したりする活動を通して、乗法の意味の理解を確実にする。
▼
第5時 乗法の答えは、被乗数を乗数の数だけ累加して求められることを理解する。
▼
第6時 倍の意味を知り、ある量の何倍かに当たる量を求めるときもかけ算を用いることを理解する。
▼
第7時 単元の学習の活用を通して事象を数理的に捉え、論理的に考察し、問題を解決する。
▼
(2)5の段、2の段の九九
第8時 5の段の九九の構成のしかたを理解する。
▼
第9時・第10時 5の段の九九を確実に唱え、適用することができる。
▼
第11時 2の段の九九の構成のしかたを理解する。
▼
第12時・第13時 2の段の九九を確実に唱え、適用することができる。
▼
(3)3の段、4の段の九九
第14時 3の段の九九の構成のしかたを理解する。
▼
第15時・第16時 3の段の九九を確実に唱え、適用することができる。
▼
第17時 4の段の九九の構成のしかたを理解する。
▼
第18時・第19時 4の段の九九を確実に唱え、適用することができる。
▼
第20時 問題づくりによる、式の読みや式に表現することを通して、5、2、3、4の段の九九の理解を深める。
▼
第21時・第22時 学習内容の定着を確認するとともに、数学的な見方・考え方をふり返り、価値付ける。
本時のねらい
「1つ分の数」「いくつ分」を捉え、「1つ分の数」と「いくつ分」の関係の場合に乗法が用いられることを知り、乗法の意味を理解する。
評価規準
「1つ分の数」と「いくつ分」の関係の場合に乗法が用いられることを理解している。
本時の展開
まいこさんは遠足で遊園地に来ました。まいこさんの学校のお友達は、どんな乗り物に乗っているでしょう。全部で何人乗っているか数えてください。今から見せます。1つ目はゴーカートです(電子黒板に観覧車の絵を写し、ぱっと消す)。
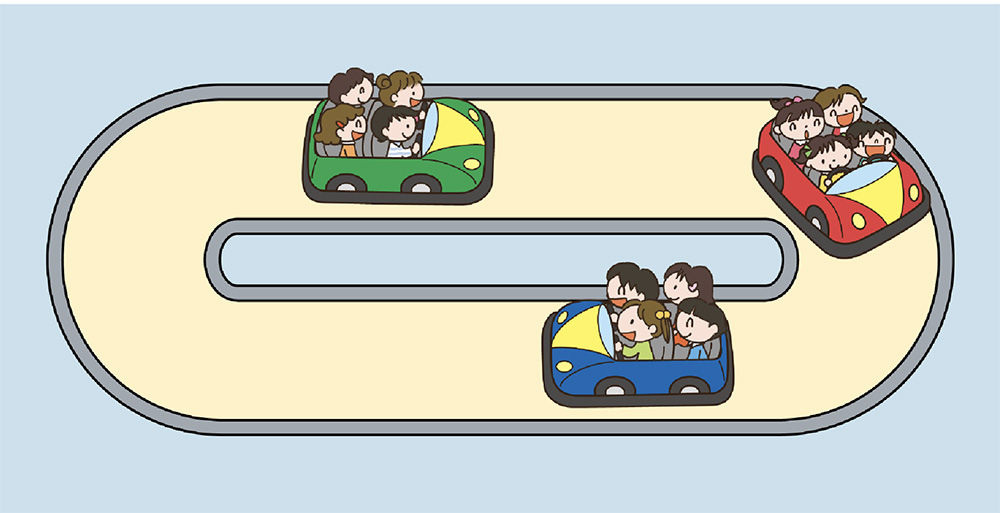
何人いたか分かりました。12人です。
すごい! 確かに12人ですね。どうしてすぐに分かったのですか。
1台に4人乗っていて、それが3台あったからです。
では、次は観覧車です(電子黒板に観覧車の絵を写し、ぱっと消す)。
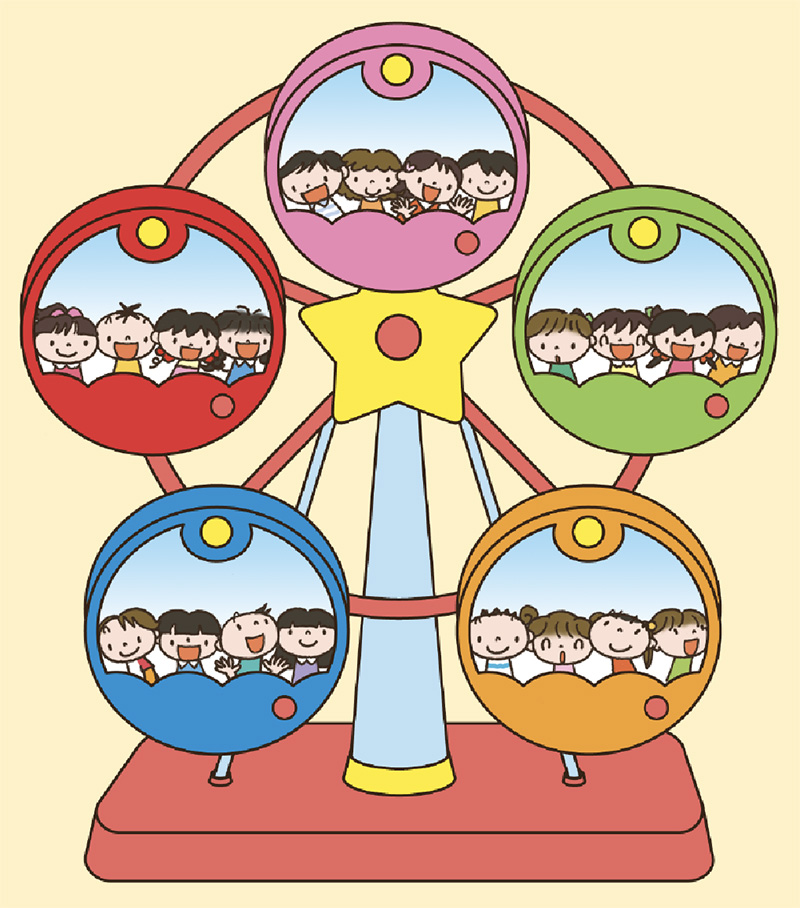
これも分かりました。1台に4人乗っていて、5台あるから20人です。
次はボートです(電子黒板にボートの絵を写し、ぱっと消す)。
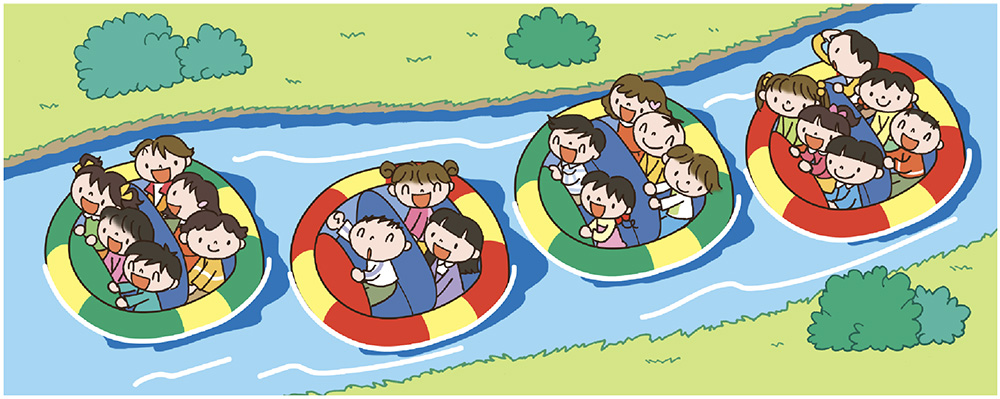
あれ? さっきと違います。
分かりません。
これじゃ数えられません。

ゴーカート・観覧車に乗っている人数は数えやすくて、ボートに乗っている人数が数えにくいわけを考えよう。
見通し
どこを見るとよいかな。
それぞれ何人ずつ乗っているのかな。
自力解決の様子
子供たちにゴーカートや観覧車、ボートが描かれたワークシートを配る。
A つまずいている子
1台の人数に目を向けることができず、なぜ数えにくいのかよく分かっていない。
B 素朴に解いている子
1台に乗っている人数が同じだと全部の数を数えやすいが、1台に乗っている人数がみんな違うと、全部の数が数えにくいことに気付いている。
C ねらい通り解いている子
1台に乗っている人数が同じだと、それがいくつあるか分かれば全部の人数を数えることができるが、1台に乗っている人数がバラバラだと、1台ずつ何人乗っているか数えなければならないため、手間がかかることを理解している。
学び合いの計画
自力解決では、ワークシートに描かれた乗り物の1台分に○を付けて、1台に乗っている人数に着目したり、1台分に何人乗っていて、それがいくつあるのか、1台ずつに人数をかき込んだりして、いくつ分かに着目している姿があったら、その様子を発表・検討場面で生かせるように、板書しておきます。
イラスト/横井智美、やひろきよみ