小4算数「がい数」指導アイデア
執筆/福岡教育大学附属久留米小学校教諭 廣木伸幸
編集委員/文部科学省教科調査官・笠井健一、福岡教育大学教授・清水紀宏
目次
本時のねらい(本時6/8時 単元展開)
四捨五入をして概数にする前の、元の数の範囲を求めることができる。また、「以上」「未満」「以下」の意味を知る。
評価規準
四捨五入して求めたい位までの概数にしたときに、ある概数になる整数の範囲を求め、「以上」などの言葉を使って表すことができる。(知識・技能)
問題
今週の図書館の利用者数を四捨五入して、十の位までのがい数にすると、約630人でした。約630になる整数について考えましょう。
図書委員会からの放送で、今週の図書館の利用者は約630人ということでしたね。正確には何人でしょうね。
632人かな。
625人とか。
625人は約630人になるのかな。
なるほど。では今日は(問題場面を提示して)、約630と言えるのは、どのような数か調べてみましょう。
学習のねらい
四捨五入して、求めたい位までのがい数になる整数について調べよう。
見通し
- 十の位の数や一の位の数に目を付けるとよい。〔着眼の見通し〕
- 数直線を使って調べる。〔方法の見通し〕
- 625から635までではないかな。〔結果の見通し〕
自力解決の様子
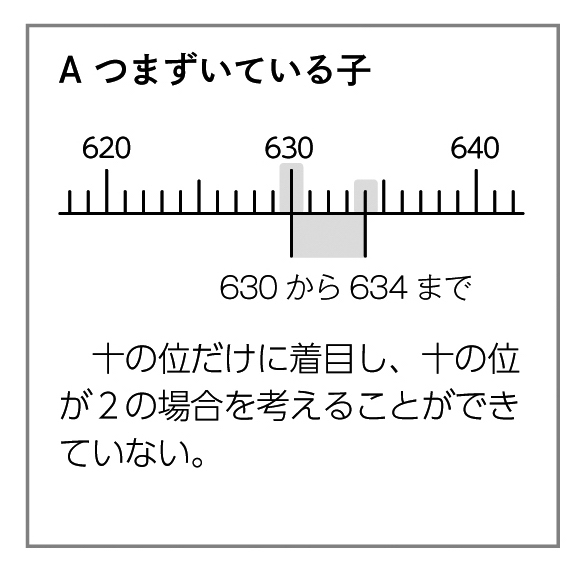
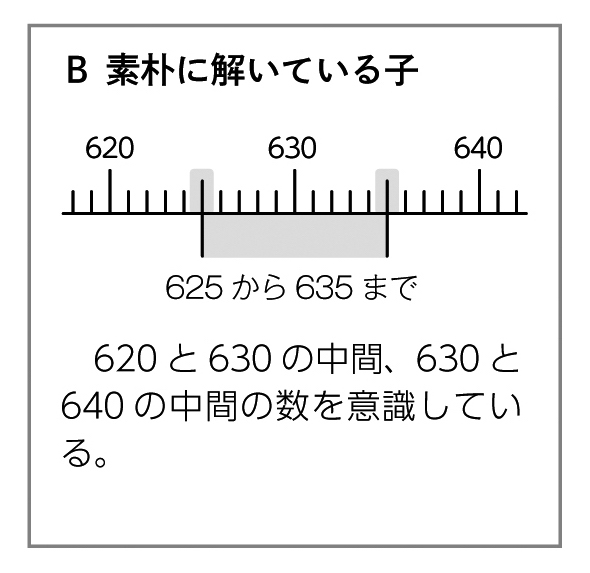
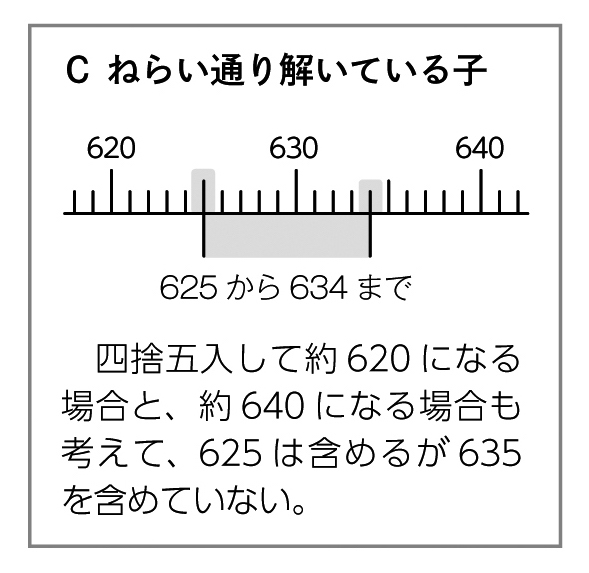
学び合いの計画
イラスト/横井智美
『教育技術 小三小四』2021年8/9月号より






