小5算数「整数の性質」指導アイデア《公約数を活用した問題解決》
執筆/福岡県北九州市立港が丘小学校教諭・塩谷順平
監修/文部科学省教科調査官・笠井健一、福岡教育大学教授・清水紀宏

目次
単元の展開
第1時 二つに分けられた整数の特徴に着目し、その分け方を考える。
▼
第2時 整数が2で割り切れるかどうかに着目し、整数が偶数と奇数に類別できることを知ること。
▼
第3時 偶数と奇数を乗法の式に表し、その意味や性質を考える。
▼
第4時 倍数の意味を理解する。
▼
第5時 公倍数、最小公倍数の意味を理解する。
▼
第6時 公倍数の意味や性質に着目し、公倍数の求め方を考える。
▼
第7時 二つの数の公倍数の求め方を基にして、三つの数の公倍数の求め方を考える。
▼
第8時 約数の意味を理解する。
▼
第9時 公約数、最大公約数の意味を理解する。
▼
第10時 公倍数の意味や性質に着目し、公約数の求め方を考える。
▼
第11時(本時) 公約数を活用し、問題を解決する。
▼
第12時 学習内容のふり返りと定着
本時のねらい
日常場面の問題を、公約数を用いて解決することができるようにする。
評価規準
公約数を使って、問題をよりよく解決することができる。(思考・判断・表現)
本時の展開

下のような、たて18㎝、横12㎝の方眼紙があります。方眼紙の目盛りは1㎝です。この方眼紙を目もりの線にそって切って、紙のあまりが出ないように、できるだけ大きな同じ大きさの正方形に分けたいと思います。正方形の1辺はなん㎝でしょうか。
※太字の部分は、最初は隠しておく。
この問題で扱われている「方眼紙」という素材や正方形という形は、子供にとって身近なものです。とはいえ、この問題場面のような活動を、子供たちが日常的に多く行うわけではないでしょう。そこで、まずはこの問題場面を確実に理解させることが大切になります。
そのために、問題文の一部を最初は隠しておき、同じ大きさの正方形に分けるということをイメージさせるとよいでしょう。本実践では、ICTを活用して、子供たちにとって比較的理解しやすい数値(1㎝、2㎝)で、この問題場面のイメージをつかませます。
また、明らかにうまくいかない場合(10㎝)を提示することで、18や12を「あまらないように分ける」こと、すなわち約数や公約数に着目させることにつなげていきます。
※縦18㎝、横12㎝の方眼紙を子供たちに1枚ずつ配付する。
この方眼紙を同じ大きさの正方形に分けましょう。方眼紙だから確実な分け方が一つありますが、分かりますか。
一辺が1㎝のときは、分けられると思います。
※ICTを活用して、タブレットやテレビに分けた状態を示す。

全部、一辺が1㎝の大きさの正方形になっていますね。では、一辺が1㎝でないと、同じ大きさの正方形に分けられませんか。
2㎝でもできそうです。
できるでしょうか。
※ICTを活用して、一辺が2㎝の場合を映す。
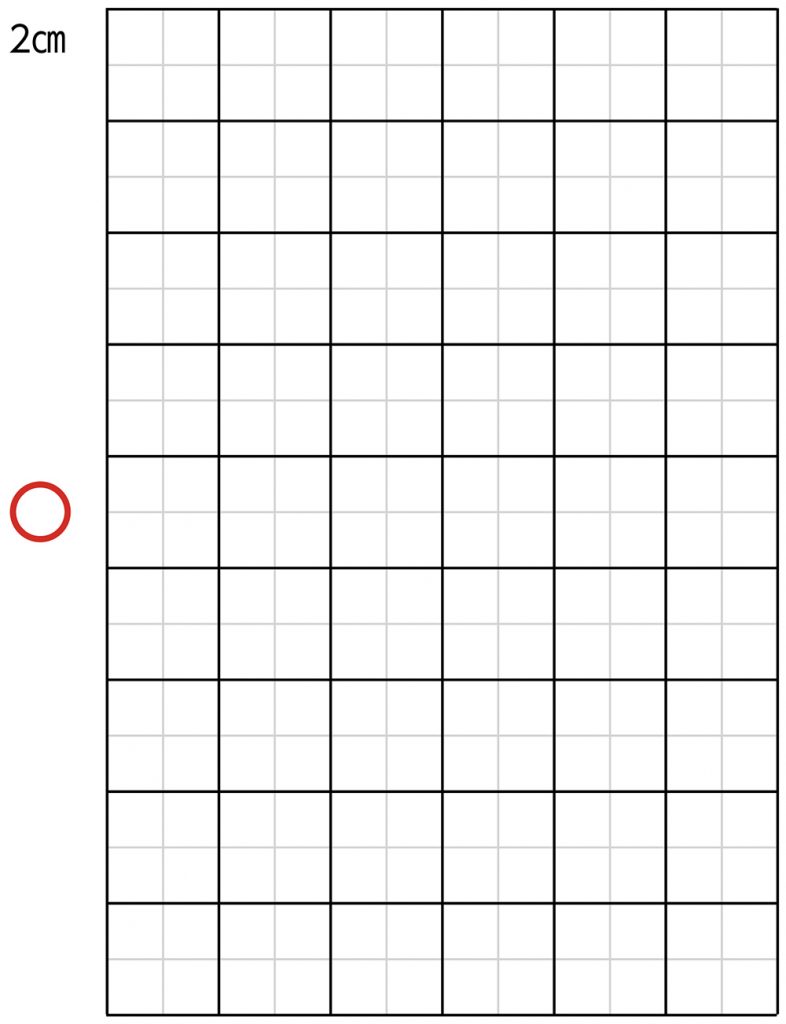
やっぱりできた。
10㎝のときはどうでしょうか。隣の友達と相談してみましょう。
(相談後)できないと思います。
もう少し詳しく説明できますか。
一つしか正方形ができないと思います。
紙があまると思います。
※ICTを活用して、一辺が10㎝の場合を映す。
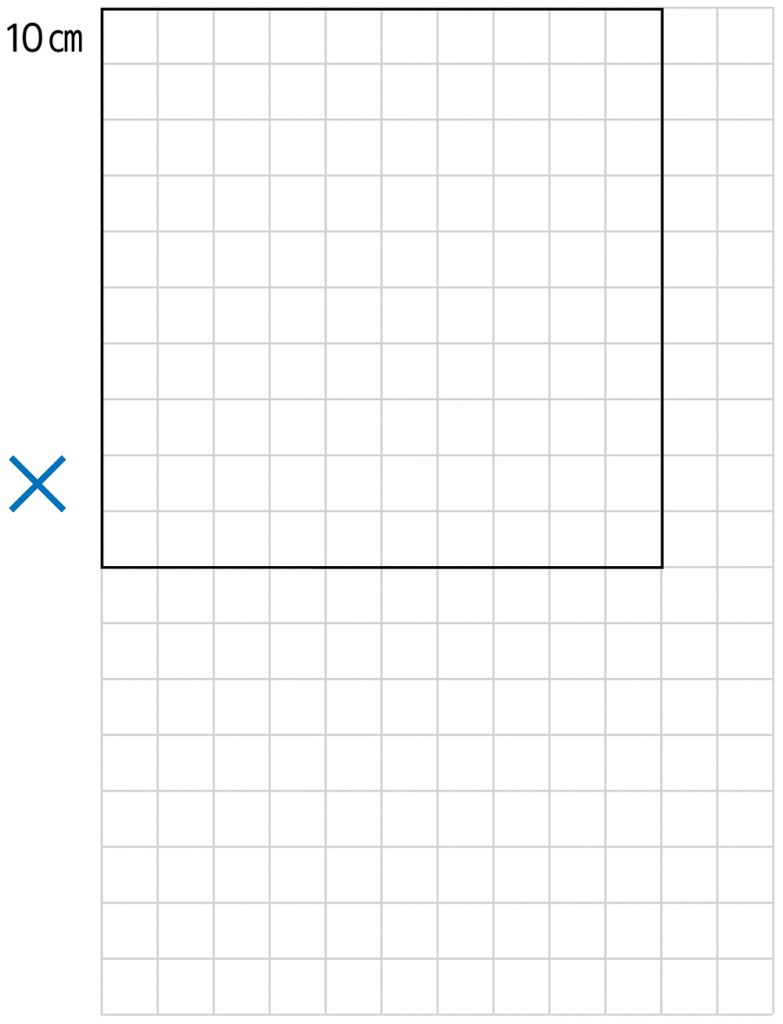
確かに、一辺が10㎝の正方形が、一つしかできないようですね。さっき、紙があまると言ってくれましたが、数を使ってもう少し詳しく説明できますか。
縦が18㎝だから18―10=8で、縦が8㎝あまります。
横も12―10=2で、2㎝あまります。
同じ正方形で分けていくとき、紙にあまりがない場合と、あまりがある場合がありますね。それでは、今日の問題です(問題文の隠していた箇所を見せる)。この問題の条件は、次の三つになりますね(子供とのやりとりで条件を確認する)。
条件
①同じ大きさの正方形に分ける。
②あまりが出ないように分ける。
③できるだけ大きくする。

条件に合うような正方形の分け方を調べよう。
自力解決の様子
A つまずいている子
・12や18の約数に着目することができない。
・12や18の約数を調べればよいことには気付いているが、12と18の公約数を求めればよいことに気付かない。
〈解答例〉
12の約数は1、2、3、4、6、12
答え 6㎝
B 素朴に解いている子
・12と18の公約数を求めればよいことに気付き、それぞれの約数を求めてから、公約数を見付ける。
〈解答例〉
12と18の最大公約数を求めます。
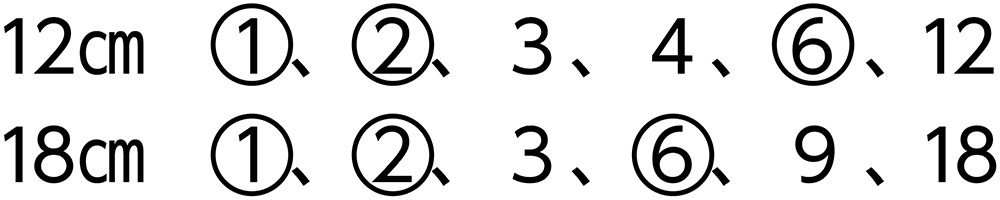
答え 一辺が6㎝の正方形
C ねらい通り解いている子
12と18の公約数を求めればよいことに気付き、一方の約数を求めてから、もう一方の公約数になっているかどうかを大きい数から調べ、最大公約数を見付ける。
〈解答例〉
12の約数を求めてから、大きい順に18の約数かどうか調べる。
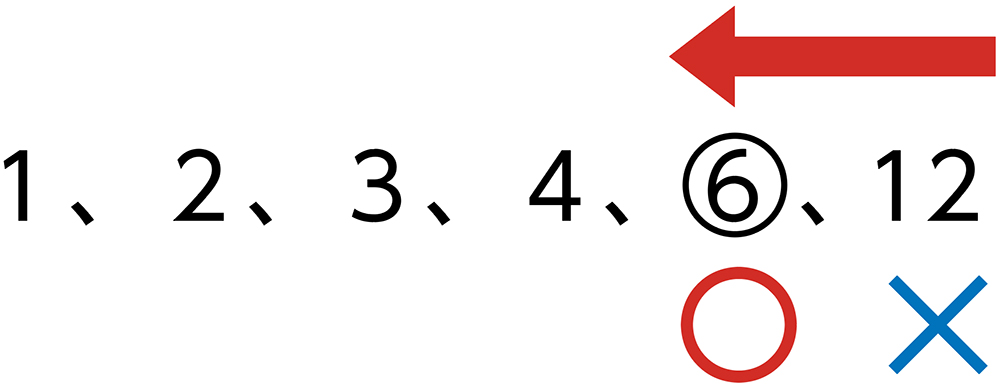
答え 一辺が6㎝の正方形
ノート例
イラスト/横井智美