小6算数「分数のわり算」指導アイデア《分数÷分数の計算方法を考えよう》
執筆/東京都公立小学校教諭・工藤倫子
編集委員/文部科学省教科調査官・笠井健一、東京都公立小学校校長・長谷豊
目次
本時のねらいと評価規準
(本時の位置 2/10)
ねらい
分数÷分数の計算の仕方を考え、説明することができる。

評価規準
・既習の整数や小数の除法や計算のきまりを活用し、分数の除法の計算の仕方を進んで考えようとしているか。
・分数÷分数の計算の仕方を、既習の計算や数直線を用いて考え、筋道立てて説明しようとしているか。
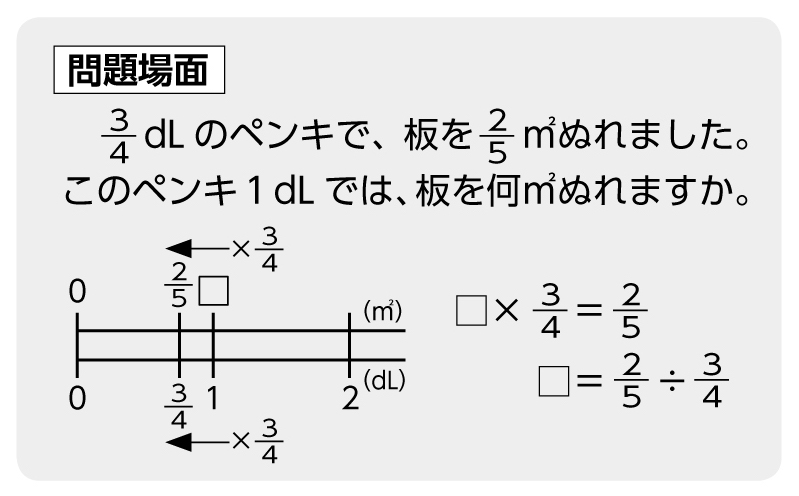
前の時間に1にあたる大きさを求める時、わる数が分数でも整数や小数と同じようにわり算の式になることを学習しました。今日は、その計算の仕方を考えて、1dLで何㎡ぬれるか調べてみようと思います。
式はどのような式になりましたか。
[MATH]\(\frac{2}{5}\)[/MATH]÷[MATH]\(\frac{3}{4}\)[/MATH] です。
今までのわり算と違うところはどこですか。
わる数が分数になっているところです。
わる数が分数でも計算できるのかな?
本時の学習のねらい
[MATH]\(\frac{2}{5}\)[/MATH]÷[MATH]\(\frac{3}{4}\)[/MATH] の計算の仕方を考えよう。
見通し
どうすれば1dLで何㎡ぬれるかをもとめられそうですか。
[MATH]\(\frac{3}{4}\)[/MATH]Lは[MATH]\(\frac{1}{4}\)[/MATH]dLが3つ分だから、[MATH]\(\frac{1}{4}\)[/MATH]dLでは何㎡ぬれるかを考えてみたらできないかな?
わる数が小数の時みたいに、[MATH]\(\frac{3}{4}\)[/MATH]も整数になおせないかな?
わる数を1にできないかな?
自力解決の様子



学び合いの計画
前時で、[MATH]\(\frac{3}{4}\)[/MATH]dLが2dLや3dLだったらという場面を提示しているので、それを活用し、「わる数が整数だったら計算できるのに…」というイメージをもたせたいものです。そのために、「[MATH]\(\frac{3}{4}\)[/MATH]dLが、どんな数だったら計算できそうかな?」や「[MATH]\(\frac{3}{4}\)[/MATH]dLをどのようにしたら整数にできるかな?」などの声かけをしていきましょう。
イラスト/横井智美
『教育技術 小五小六』 2020年6月号より

