小5算数「正多角形と円」指導アイデア
執筆/お茶の水女子大学附属小学校教諭・岡田紘子
編集委員/文部科学省教科調査官・笠井健一、東京都公立小学校校長・長谷豊
目次
本時のねらいと評価規準
本日の位置 2/9
ねらい
正多角形と円の特徴を活用して、正八角形を作図することができる。
評価規準
円の中心の周りの角度に着目し、正多角形を作図することができる。

(前時に作成した正八角形の紙を見せながら)前の時間に学習した正八角形は、どんな特徴がありましたか?
8つの辺の長さがすべて等しくて、8つの角の大きさもすべて等しいです。
正八角形の角の大きさは、すべて135°でした。
円の形の紙を折って正八角形を作ったとき、8つの合同な二等辺三角形ができました。
正八角形の中心から、頂点まではすべて同じ長さでした。
今日は、円を使って正八角形をかいてみましょう。前の時間に見つけた正八角形の特徴を使って、かき方を考えましょう。
本時の学習のねらい
円を使って正八角形のかき方を考えよう。
見通し
円の中に、合同な二等辺三角形を8個かけばできると思います。
正八角形の角の大きさは、135°であることを使えないかな。
円の中心の周りの角を8等分すればかけそう。
自力解決の様子
A つまずいている子
円の中心の周りの角を8等分する方法がわからない。
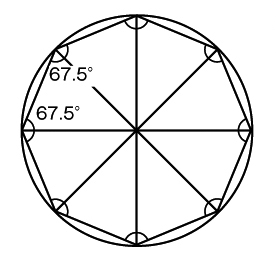
B 正八角形の角が135°であることを基に、135÷2=67.5°であることを基にかき方を考える子
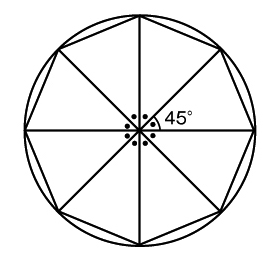
C 中心にある角の大きさに着目し、中心の角を360÷8=45と計算し、中心が45°の合同な二等辺三角形を用いて、正八角形のかき方を考える子
学び合いの学習
前時では、円形の紙を用いて正多角形を作り、その特徴を調べる活動を行う。前時で見いだした正多角形の性質や特徴を基に、本時では、正多角形のかき方を考えさせていく。はじめに、円形の紙を用いて作成した正八角形を提示する。そして、正八角形の性質や特徴を振り返る場を設ける。前時を振り返ることで本時の課題の見通しをもたせ、辺の長さがすべて等しいこと、すべての角の大きさが等しいことに加え、8個の合同な二等辺三角形で正八角形が構成されていることに着目させる。
イラスト/横井智美
『教育技術 小五小六』 2020年2月号より






