小6算数「角柱と円柱の体積」指導アイデア
執筆/神奈川県公立小学校教諭・三上顕
編集委員/文部科学省教科調査官・笠井健一、島根県立大学教授・齊藤一弥

目次
本時のねらいと評価規準
[本時の位置 2/5 三角柱の求積]
ねらい
図形を構成する要素に着目し、三角柱の体積の求め方を見いだすとともに、その表現を振り返り、簡潔かつ的確な表現に高めることができる。
評価規準
三角柱の面積の求め方を、既習の計算によって体積を求める考えに帰着させて考えている。
問題場面
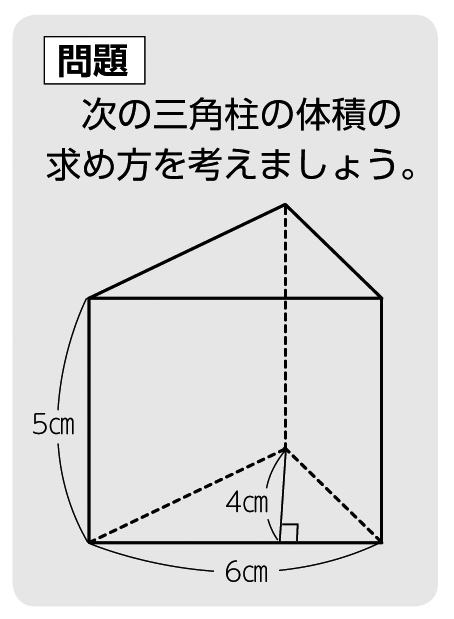
これまでに、どんな立体の体積を求めてきましたか。
直方体や立方体の体積を求めました。
四角柱の体積も求めました。
直方体や立方体の体積は、どのように求めてきましたか。
直方体は、縦×横×高さで求めました。立方体も、一辺×一辺×一辺で求めました。
底面積×高さとみても、求められました。
つまり、かけ算を使って求めてきましたね。今回の三角柱も、かけ算を使って求められるかな。
底面を見ると、1つ分の大きさが違うので、かけ算が使えません。
でも、面積の時と同じように、工夫すればできそうだ。
三角柱の体積も、かけ算を使って工夫して求めてみましょう。
本時の学習のねらい
三角柱の体積を求め、説明しよう。
見通し
〈方法の見通し〉
三角形の面積を求めたときと同じように、図形を切ったり組み合わせたりするとできそうだな。
〈方法の見通し〉
三角柱の場合も、四角柱と同じように「底面積×高さ」で考えることができそうだね。
自力解決
A つまずいている子
辺の長さを、やみくもにかけて計算している。
B 素朴に解いている子
四角柱の半分とみて、図形を切ったり組み合わせたりしながら求めている。
C ねらい通りに解いている子
四角柱での解決方法から類推し、「底面積×高さ」とみて体積を求めている。
学び合いの計画
体積を求めることができただけで終わりにせず、図形を構成する要素に着目し、三角柱の体積の求め方を見いだすとともに、その表現を振り返り、簡潔かつ的確な表現に高めていきます。
イラスト/横井智美
『教育技術 小五小六』 2019年7/8月号より






