小5算数「小数のかけ算」指導アイデア
執筆／東京都公立小学校教諭・横須賀咲子
編集委員／文部科学省教科調査官・笠井健一、東京都公立小学校校長・長谷豊
目次
本時のねらいと評価規準
(本時 1・2 / 12 時間)
ねらい
小数をかけることの意味を理解し、整数×小数の計算の仕方を考える。
評価規準
既習の整数または小数×整数の計算の仕方と関連付けて、整数×小数の計算の仕方を考えている。(数学的な考え方)
問題
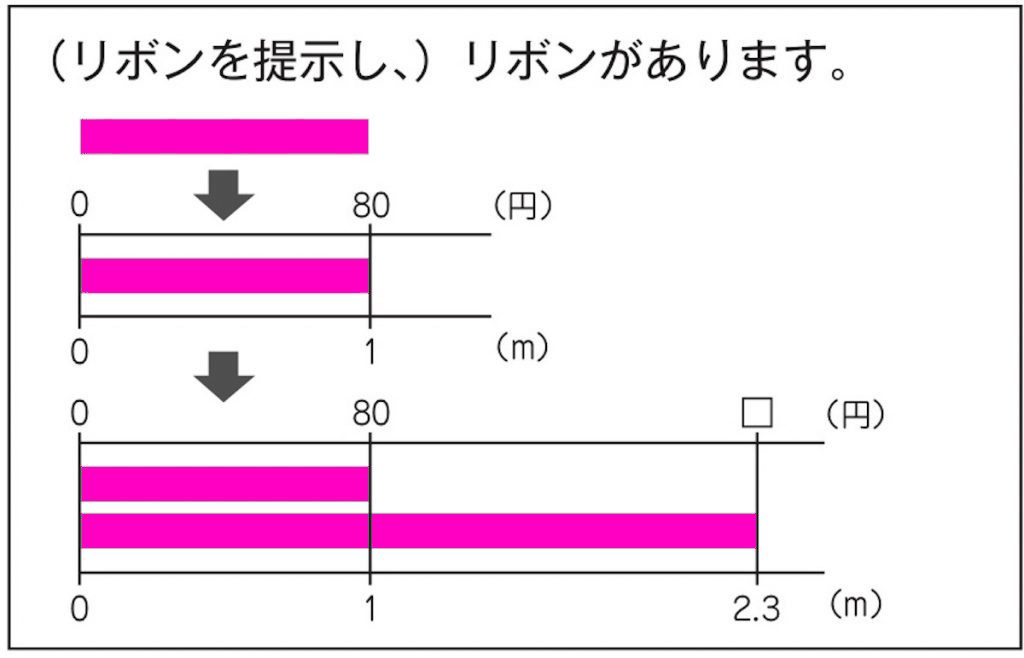
図を、文にしてみましょう。
1mの値段は、80円です。
さらに図を付け加えますよ。いくらぐらいかしら?
2mくらいだから、160円くらい。
2mより、ちょっと長そうだよ。160円よりちょっと高いから、200円くらいじゃないかな。
（図に加えて）また図を文にしてみましょう。
2.3mではいくらでしょうか。
図に合わせて、文を作るように促します。子供と一文ずつ作ることで、問題場面をしっかりと捉えさせたり、見積もりをもたせたりします。
本時の学習のねらい①
どんな式になるでしょう。
見通し
2mだったら160円と考えたのは、どうしてですか。
1mで80円ということは、 2mはその2個分だから、 80×2で160円です。
1mの値段×長さで代金が出るから、80×2で160円です。
2.3mでいくらかを求めるには、どのような式を立てればよいでしょうか。
2.3個分って言わないけれど、かけ算でいいのかな?
長さが小数になっても、1mのねだん×長さで、 80×2.3だと思います。
リボンの長さと代金は比例しているから、長さが2.3倍になると、やはり代金も2.3倍になります。図で、説明します。
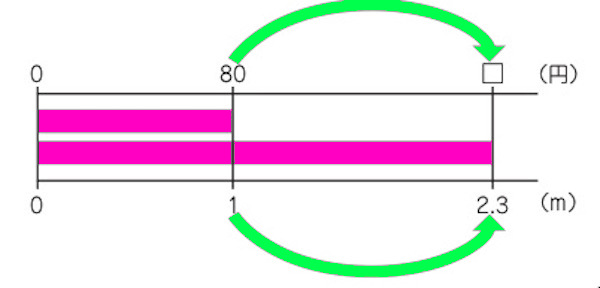
だから、長さが小数になっても、かけ算にしていいんだね!
でも、80×2.3って、どうやって計算するのだろう?
本時の学習のねらい②
80×2.3の計算のしかたを、考えましょう。
自力解決の様子
自力解決の際、手がつけられずにいる子供を集めて、今までの学習との違いである「かける数が小数であること」を確認し、「2.3を整数にするためにはどうしたらよいか」を考えさせ、2.3を10倍することを気付かせていきます。
学び合いの計画
自力解決の際、しばらくたっても手がつけられずにいる子供には、机間を静かに回って友達のノートを見て回ってもよいことを伝えます。そのようにすると、友達のノートから考えるきっかけをもらえることがあります。
イラスト／横井智美
『教育技術 小五小六』2019年５月号より
