小5算数「整数と小数」指導アイデア《整数と小数のしくみを理解し、数の世界を広げよう》
執筆/東京都公立小学校教諭・内藤信義
編集委員/文部科学省教科調査官・笠井健一、東京都公立小学校校長・長谷豊
目次
本時のねらいと評価規準
(本時の位置 1/5)
ねらい
整数と小数は十進位取り記数法で表され、0から9までの数字と小数点を使うと、どんな大きさの整数や小数でも表せることを理解する。
評価規準
整数と小数が同じ十進位取り記数法で表されていることに気付き、そのしくみを理解している。

問題場面
どのような数か、説明しよう。
どんな数ですか?(封筒から、少しずつ数を出して見せていく)。

375かな? でも、3と7の間が空いているから……。
やっぱり3.75だ。五円玉? 大きさかな?
この数は、五円玉の重さ3.75gです。
四年生で学習しましたね。では、3.75はどのような数だといえますか。説明してみよう。
位の部屋で書いてみると、次のようになります。
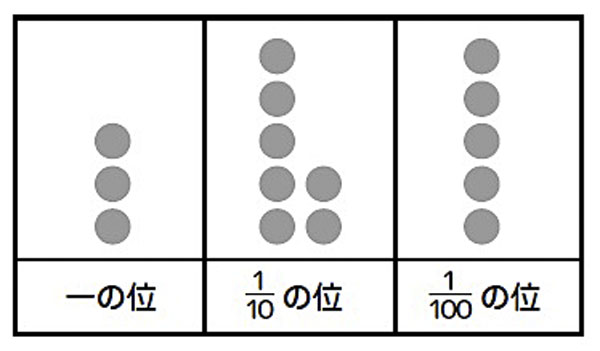
3と0.7と0.05を合わせた数です。
式で表すと 3.75=3+0.7+0.05 です。
1が3つと、0.1が7つと、0.01が5つを、合わせた数です。
0.01が375こ、集まった数です。
いろいろな表し方で、説明できましたね。では、次の数はどのような数ですか。

↓↓↓↓↓
使っている数字は同じだけれど、大きさが違う。
本時の学習のねらい
同じ数字を使っている2つの数を比べて、小数や整数のしくみを調べよう。
見通し
数のしくみを調べるために、どんな方法で2つの数を表しますか。
位ごとに、表に表そう。(A)
位ごとに、いくつ分かで言葉で表すと…。(B)
式で表すと…。(C)
自力解決の様子
A 位の部屋で、表している
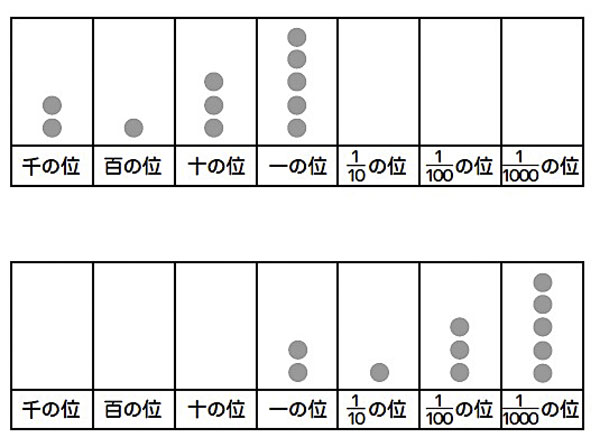
B 位ごとに、○のいくつ分かで表している
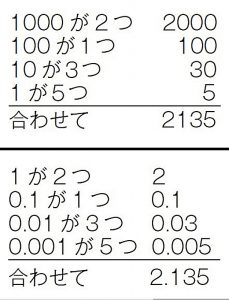
C 式で表している
2135 = 2000 + 100 + 30 + 5
2.135 = 2+0.1 + 0.03 + 0.005
学び合いの計画
本学習は第1時です。ここでは、既習を生かして解決する経験を大切にします。まず、導入では、既習の3.75のような小数について、表や言葉で位ごとに分けたり、式で表したり、多様な見方をしてきたことを振り返ります。ここで、学級の子供の実態を把握し、実態が十分でない場合は補っておきます。その上で、2135と2.135を提示します。
イラスト/やひろきよみ、横井智美
『教育技術 小五小六』2019年4月号より

