小３算数「小数」指導アイデア《数直線上の小数の表し方》

特集: 文部科学省教科調査官監修｢教科指導のヒントとアイデア｣

2025.10.27

年間指導計画

年間指導計画はこちらをクリック

・かけ算
・時刻と時間
・わり算
・たし算とひき算の筆算
・棒グラフと表
・余りのあるわり算
・長さ
・暗算
・かけ算の筆算　１けた
・１万を超える数
・円と球
・重さ
・わり算や分数
・何倍でしょう
・小数
・分数
・三角形と角
・計算の順序
・式と計算
・かけ算の筆算　２けた
・そろばん

単元の展開（各時の主な学習活動内容）

第１時　整数で表せない端数部分の大きさ（かさ(L)）の表し方
第２時　小数、小数点、整数の意味
第３時　長さ（cm）の端数部分の表し方
第４時（本時）数直線上の小数の表し方
第５時　小数第一位、小数の位取りの仕組み
第６時　小数の大小関係
第７時　小数の加法の計算の仕方
第８時　小数の減法の計算の仕方
第９時　小数第一位までの小数の加減法の筆算の仕方
第10時　小数の多様な見方や表し方
第11時　身の回りの小数を用いた問題解決

本時のねらい

１目盛りの大きさに着目して、整数と同様に数直線上の小数の読み方や表し方を考え、説明することができる。

評価規準

１目盛りの大きさに着目して、整数と同様に数直線上の小数の読み方や表し方を考え、説明している。

本時の教材のポイント

ここでは、小数を整数と同じ数直線の中に位置付けていくことで、小数の理解を深めていきます。整数の十進位取り記数法の考えを１より小さい数に拡張して、単位（１）の大きさを10等分して新たな単位（0.1）をつくり、整数と同じ数直線の中に表すことができることを学びます。

本時では、「十進位取り記数法の仕組みに着目し、小数の仕組みを整数の仕組みと統合して考えること」や「数を連続しているものと捉え、小数も整数と同様に数直線に表すことができること」などに子供が自ら気付いていけることをめざし、授業の中で子供が整数の場合と小数の場合とを行き来しながら思考を深めていけるような授業設計としました。

導入では、既習事項の想起をていねいに行います。第２学年「３けたの数」の学習から、数直線を読んだり数を表したりする際には、１目盛りの大きさに着目することが大切であることを全体で確認します。また「大きな数のしくみ」の学習で、数直線の大きい１目盛り（図の青四角）が10000を表す際のいちばん小さい１目盛りが1000であったことなど、既習の数直線の確認過程から、自然と子供が「小数の場合はどうなるのだろう」と考えや興味を進展させていけるよう指導します。

全体の話合い場面では、大きい１目盛りが１のとき赤四角の位置が1.3になる根拠を軸に子供による話合い活動を行います。話合いのねらいは大きく２つあります。

一つ目は、１が10等分されていることからいちばん小さい１目盛りが0.1であることを見いだし、赤四角が1.3であることを論理的に説明することです。これは本時のねらいに迫るものであり、１目盛りの大きさに着目して整数のときと同様に小数も数直線に位置付けることができることを学習する過程です。

二つ目は、冒頭で述べた「十進位取り記数法の仕組みに着目し、小数の仕組みと整数の仕組みを統合していく」学習過程の実現です。数直線の大きい１目盛りが1000、100、10などの既習の場合と本時で扱う１の場合とを比較する中で、いちばん小さい１目盛りが100、10、１、0.1になっていることを見いだし、小数も整数と同様の位取りの仕組みや構成になっていることに気付かせるよう指導します。これは、次時の「小数第一位」の学習につながるものであり、単元を見通した子供の自然な思考を育むものでもあります。

また、授業の中で「数を連続しているものと捉えること」を顕在化させる指導も大切です。例えば、授業の終末の場面で「１の次の数は？」と子供に問い、「２？　いや1.1？」などと小数を表す数直線を用いて、数の世界を拡張していくような話合いを学級で展開してもよいかもしれません。また、記事末の「ポイント＆アドバイス」で紹介したタブレットなどのデジタル機器を扱い、数の相対的な見方や連続的な見方に触れる指導も有効であると考えられます。

本時の展開

※数直線を提示する。

あ、数直線だ。

大きい数の授業で習いました。

赤の四角（０から数えて13の位置）に入る数はいくつでしょう。

13だと思います。

うん、０から数えて13番目にあるし、大きい目盛り（青の四角）から３大きいところにあるから。

本当にそうでしょうか。

んー、130とかかもしれない。

１目盛りが１だったら13だけど、１目盛りが100だったら1300になる。

１目盛りの大きさが1000のとき、10目盛り目で10000を表したね。

１目盛りの数が変わると、同じ数直線でも表せる数が変わったね。

※デジタル数直線を活用して、１目盛りの大きさが変わる様子や数が連続している様子を確認する。

１目盛りがいくつか分からないから、赤四角がいくつかは分からない。

青の四角がいくつか分かれば分かる。

だって、青の四角を10等分すれば、１目盛りの大きさが分かる。

じゃあ、ここ（青の四角）が１だったらどうでしょう。

え、そんな数ないんじゃない。

なんだろう。

1.3かな。

え、小数か。

1.3な気がするけど……。

小数も数直線に表すことができるのかな。

どうして赤の四角が1.3だと言えるのでしょうか。

小数を数直線に表す方法を考えよう。

見通し

青の四角の目盛り（大きい目盛り）が１だから、いちばん小さい１目盛りは……。

10000を10等分したとき、１目盛りが1000。1000を10等分したとき、１目盛りは100だったから……。

13は１が13個分。1.3は0.1が13個分だから……。

自力解決の様子

Ａ　つまずいている子

・なんとなく1.3だということは分かるが、その理由がはっきりと分からない。

Ｂ　素朴に解いている子

・０から数えて13番目だから、1.3だと考えている。

・一つ目の大きい目盛りが、10のときの数直線と比較し、10が１になっていることから、13が1.3になると考えている。

※次時の位取りの仕組みの学習につなげたい。

Ｃ　ねらい通り解いている子

・１が10等分されていることから、１目盛りの大きさが0.1であることを見いだし、それがいくつ分あるかと考えている。

ノート例

Ｃ　ねらい通り解いている子

全体発表とそれぞれの考えの関連付け

それではみんなで確認しましょう。どうしてここ（赤の四角）は1.3だと言えるのでしょう。

0.1が13個分、０から数えて13番目の目盛りだから、1.3と言えます。

１から、0.1の目盛りが３つ分進んでいるから、1.3です。

みんなが話している0.1とはどんな数ですか？

１目盛りです。

いちばん小さい１目盛りが0.1です。

数直線の０から１までの目盛りが10等分されているからです。

１を10等分したら、いちばん小さい１目盛りが0.1になります。

どうしていちばん小さい目盛りを求めたのですか。

数直線を読むときはいちばん小さい目盛りがいくつか分かれば、そのいくつ分で読めるからです。

整数のときも数直線を読むときは、いちばん小さい１目盛りが大切だったね。

いちばん小さい１目盛りがいくつを表すのかが大切でした。

（板書計画のように数直線を縦に並べて）整数の数直線と比べて気付くことはありますか。

10集まると大きい目盛りになるのは同じ。

10集まったら位が一つ上がる。

いちばん小さい１目盛りが10なら10目盛り目は100、100を10等分したら10になる。

反対に目盛りを小さくするのには、10等分する。

目盛りを小さくするのに10等分するのは整数も小数も同じかも。

10等分すると、位が一つ下がった目盛りがつくれるのだ。

今回だったら、10等分すると整数と整数の間に0.1（小数）をつくることができた。

数直線を縦で比べると、０が１つずつ減っている。

大きい目盛りが10の数直線と比べると、いちばん小さい目盛りが１じゃなくて0.1になっている。

大きい目盛りが10のとき、いちばん小さい目盛りは１になっていて、大きい目盛りが１のとき、いちばん小さい目盛りは0.1になっているね。

整数のときのように、位が一つ下がっている？　0.1の位ということだと思う。

学習のまとめ

数直線を読んだり、書いたりするときは、いちばん小さい１目盛りの大きさが大切。
いちばん小さい１目盛りを0.1にすると、小数も整数と同じように数直線に表すことができる。
大きい１目盛り目を10等分すると、小さい１目盛りの数が分かる（位が一つ下がる）。

評価問題

（１）□にあてはまる数をかきましょう。
　　　①3.6は、0.1を□こ集めた数です。
　　　②0.1を21こ集めた数は□です。

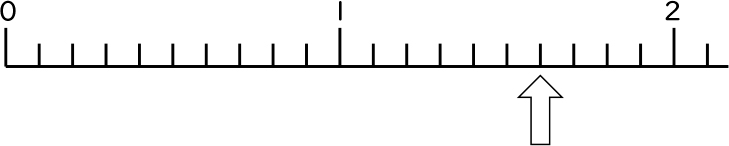
（２）下の数直線の矢印が表す数はいくつですか。また、その理由もかきましょう。

（３）下の数直線の、0.7に印をつけましょう。

子供に期待する解答の具体例

（１）①36個　②2.1

（２）1.6
　　　理由は、いちばん小さい１目盛りが0.1で、それが16個分ある（16番目だ）から。

（３）

感想例

小数も整数と同じように考えて数直線に表すことができると分かった。数直線にすると、整数と整数の間に小数が入ることが分かりました。小数と小数の間にはどんな数が入るのか気になりました。
数直線を読んだり表したりするときは、いちばん小さい１目盛りの大きさが大切だと改めて思いました。大きい目盛りを10等分して、小さい１目盛りの大きさを求めることができました。
10等分すると位が下がるなら、一の位より下の位について調べたい。