小5算数「円と正多角形」指導アイデア《円を使って正六角形をかく》
執筆/横浜市立霧が丘義務教育学校前期課程・青木真璃奈
監修/文部科学省教科調査官・笠井健一
島根県立大学教授・齊藤一弥

目次
単元の展開
第1時 辺や角に着目し、正多角形の定義や性質を理解する。
▼
第2時 正多角形の性質に基付き、円の中心の周りの角を等分して正多角形をかく方法を考える。
▼
第3時(本時)正多角形や円の定義や性質に基づき、円を使って正六角形をかくことができる理由を考え、説明することができる。
▼
第4時 正多角形の性質に基づき、円周と直径の関係について考える。
▼
第5時 円の直径の長さと円周の長さの関係について考える。
▼
第6時 円周率について知り、円周の長さや直径の長さを求める問題を解決する。
▼
第7時 円周の長さと直径の長さの関係を、比例という観点から捉える。
▼
第8時 本単元の学習内容の定着及び円周の長さを活用する問題を解決する。
本時のねらい
図形の構成要素に着目して、正多角形や円などの既習の図形の定義や性質に基づき、円を使って正六角形をかくことができる理由を考え、説明することができる。
評価規準
正六角形を構成している正三角形の辺の長さや角の大きさに着目し、円の性質と関連付けながら、正六角形がかける理由を考え、説明している。
本時の展開

正八角形と同じように正六角形が作図できるか考え、説明しよう。
前回の授業では何をしましたか。
正八角形をかきました。
どうやったら正八角形をかくことができましたか。
円周上に8つの点を決めればかけました。
どうして、正八角形は円周上にあると分かったのですか。
正八角形の対角線同士を結んでできた中心Oから頂点までの距離が同じ長さだったからです。
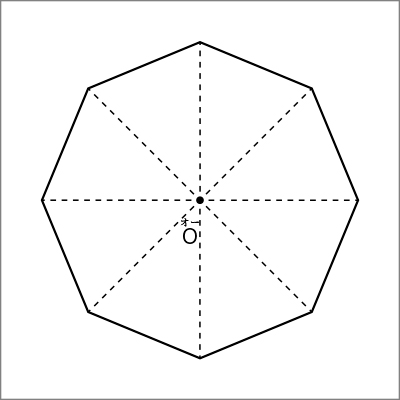
そこから、円周上に8つの点を決めることができれば、正八角形がかけると分かったのですね。では、どうやって8つの点を決めたのですか。
円の中心の周りの角を8等分しました。
8等分すると1つ分の角度は何度になりましたか。
360°÷8=45°で、45°になりました。
分度器で45°を測りながら半径をかき、円と交わったところを8つの点を決めました。
45°を測って、二等辺三角形をかいて、その底辺と同じ長さをコンパスで測りとって、印をつけていく方法もありました。
どうして、その方法が使えるのですか。
正八角形は、合同な二等辺三角形が8個でできている図形だからです。
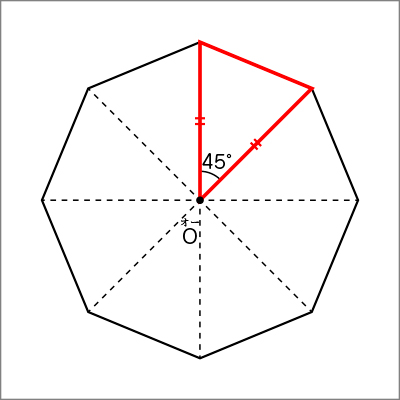
正八角形の性質と円の性質を使ったら、正八角形はかくことができたのですね。
正八角形以外もかけます。
正八角形以外もかくことができるのですか。
同じようにすれば、正六角形などもかけるはずです。
では、今日は正六角形も同じようにかけるか、試してみましょう。

正八角形と同じように、図形のどんな性質を使えば正六角形がかけるか考え、説明しよう。
見通し
正八角形のときは、円の周りの角を8等分したから、今回は6等分すればかけそうだな。(方法の見通し)
合同な三角形が6個あるはずだから、それを使えばかけそうだな。(方法の見通し)
正八角形でやったことと同じようにすれば、正六角形もかけそうだ。(結果の見通し)
自力解決の様子
A つまずいている子
円の周りの角を6等分し、毎回分度器を使って、60°を測りながら、円周上の6つの点を決めている。
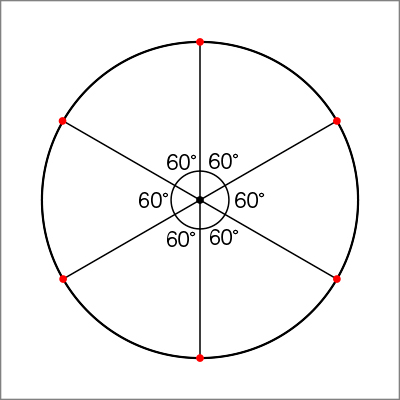
B 素朴に解いている子
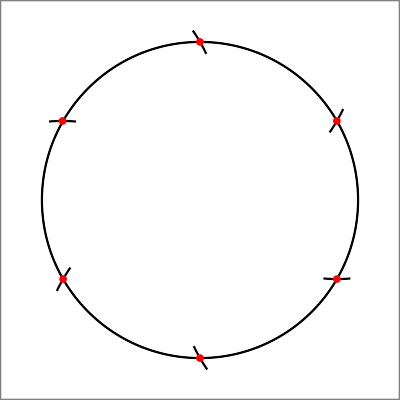
正八角形の作図を活用し、底辺と同じ長さをコンパスで測りとりながら円周上に6つの点を決めている。
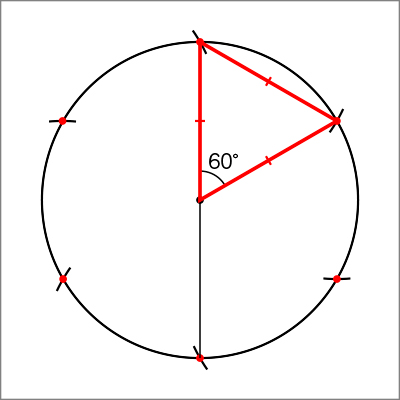
C ねらい通り解いている子
正六角形が6つの正三角形で構成されていることに気付き、円の半径の長さと正三角形の一辺の長さが等しくなることを使って、円周上に6つの点をとることができている。
学び合いの計画
前時の学習では、正八角形の作図を行いました。そこでは、正八角形の頂点が円周上にあること、8個の合同な二等辺三角形で構成されていることに着目して考えています。
本時の学習では、前時の正八角形の作図をふり返り、その過程や結果から類推して、正六角形を作図する活動から始めます。正八角形の作図の方法と正六角形の作図の方法を比較したり、作図にどのような性質を活用したかについて明らかにしたりしていくことを通して、正多角形の性質の理解をさらに深めましょう。また、正六角形は、合同な正三角形が6つで構成されている図形であるため、他の正多角形とは異なり、角度を測らなくても作図をすることができる図形です。作図方法を比較することで、既習の図形の性質や合同な図形の性質を活用することが、労力を減らして考えることにつながることを実感させましょう。そうすることで、既習の図形の性質を活用することのよさに気付けると考えます。
また、「いつでも使えるか?」という視点で作図をふり返ると、半径の長さだけを使ってかく方法は正六角形の作図の際には極めて有効ですが、他の正多角形の作図には適用できません。作図の方法を比較することで、正三角形と二等辺三角形の性質の違いにも改めて気付くことができるので、「いつでも使えるのか」「どんな正多角形でも使えるのか」という視点でふり返ることも大切にしましょう。
考えの共有の場面や、適用問題で「他の正多角形をかけるか」について試す場面では、1人1台端末の活用が有効になります。その際には、ただ友達の考えを見るのではなく、自分のかき方と「同じか、違うか」という視点や、違うとしたら「相手はどのように考えてかいたのか」と考える視点をもたせることが大切です。比較を通して、相手の考え方を学んだり、よりよい考えはどれかについて子供自身が考えられる機会を増やしたりすることで、自分の答えに満足することなく、よりよいものを求めようとする子供の姿にもつなげていきます。
ノート例
A つまずいている子
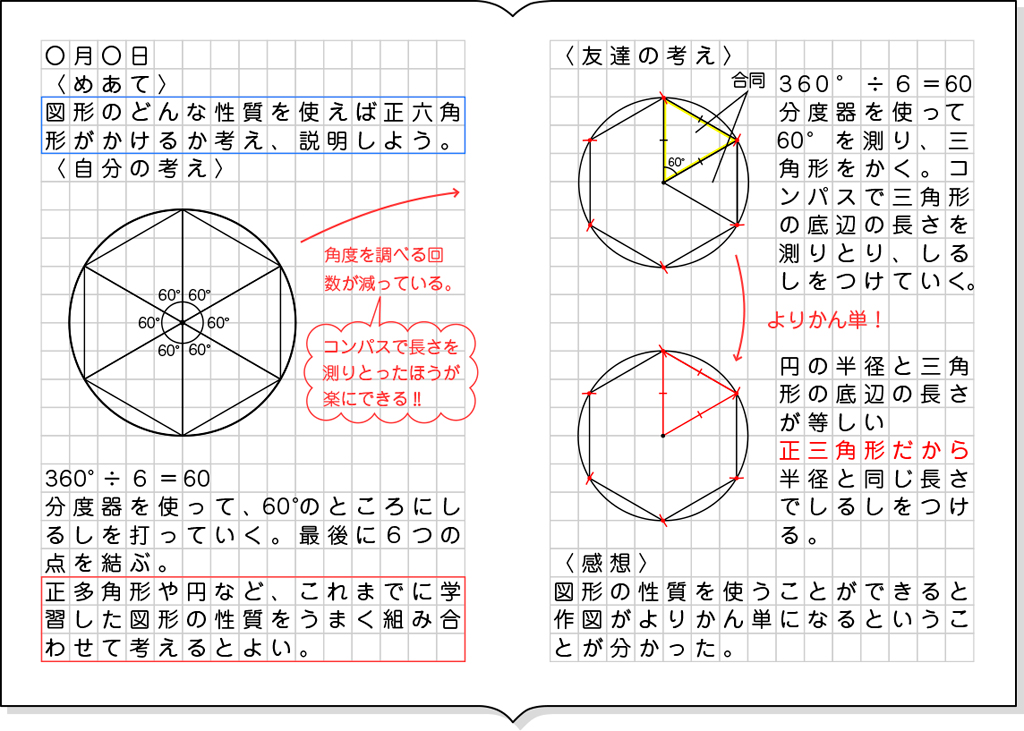
B 素朴に解いている子
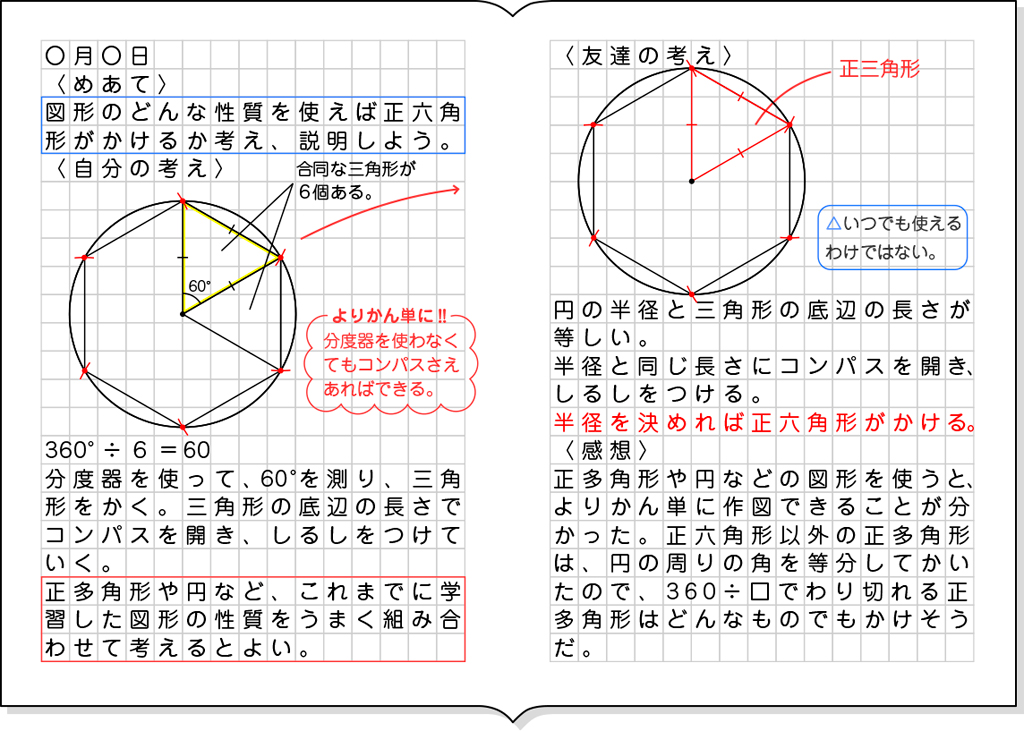
全体発表とそれぞれの考えの関連付け
※C1、C2、C3のそれぞれが発表をする。
C1
円の周りの角は360°です。それを6等分すると360÷6=60で60°になります。分度器を使って、60°を測って印をつけるということを6回繰り返して、6つの点を決めるとかくことができました。
C2
正八角形の作図と同じように考えます。正六角形は合同な三角形が6つでできているので、分度器で60°を測って、三角形をかきます。その三角形の底辺と同じ長さをコンパスで測りとりながら、円周上に6つの点を決めるとかくことができました。
C3
正六角形は合同な正三角形が6つでできています。正三角形は3つの辺の長さが等しいので、円の半径の長さと正三角形の1辺の長さが等しくなります。コンパスを半径の長さに開いたまま、円周上に印をつけていくと6つの点が決まり、図形をかくことができました。
3つの考えを比べると、よりよいと思うのはどれですか。
イラスト/横井智美

