小４算数「面積」指導アイデア《長方形や正方形の面積の求め方》

特集: 文部科学省教科調査官監修｢教科指導のヒントとアイデア｣

2025.01.29

単元の展開

第１時　図形を構成する正方形や長方形の数に着目し、面積の比べ方を考える。
▼
第２時　面積の意味、単位「平方センチメートル（㎠）」を知る。
▼
第３時（本時）１㎠のますの数に着目し、長方形や正方形の面積を求める公式を考える。
▼
第４時　面積の公式を適用して、面積を求める。
▼
第５時　長方形を組み合わせた図形について、構成する長方形、正方形に着目し、面積の求め方を考える。
▼
第６時　基にする広さに着目して、大きな面積の表し方を考える。
▼
第７時　１ｍ＝100㎝であることに着目し、１㎡＝10000㎠であることを考える。
▼
第８時　面積の単位「アール（a）」「ヘクタール（㏊）」「平方キロメートル（㎢）」を知る。
▼
第９時　正方形の１辺の長さに着目し、単位の相互関係を考える。
▼
第10時　表や折れ線グラフに着目して、縦の長さと面積の関係を考える。
▼
第11時　学習内容の習熟や定着、数学的な見方・考え方のふり返りを行う。

本時のねらい

長方形や正方形の面積を計算で求める方法を考え、公式を導くことができる。

評価規準

辺の長さと１㎠の正方形の数の関係に着目して、長方形や正方形の面積の求め方を考えたり説明したりしている。

本時の展開

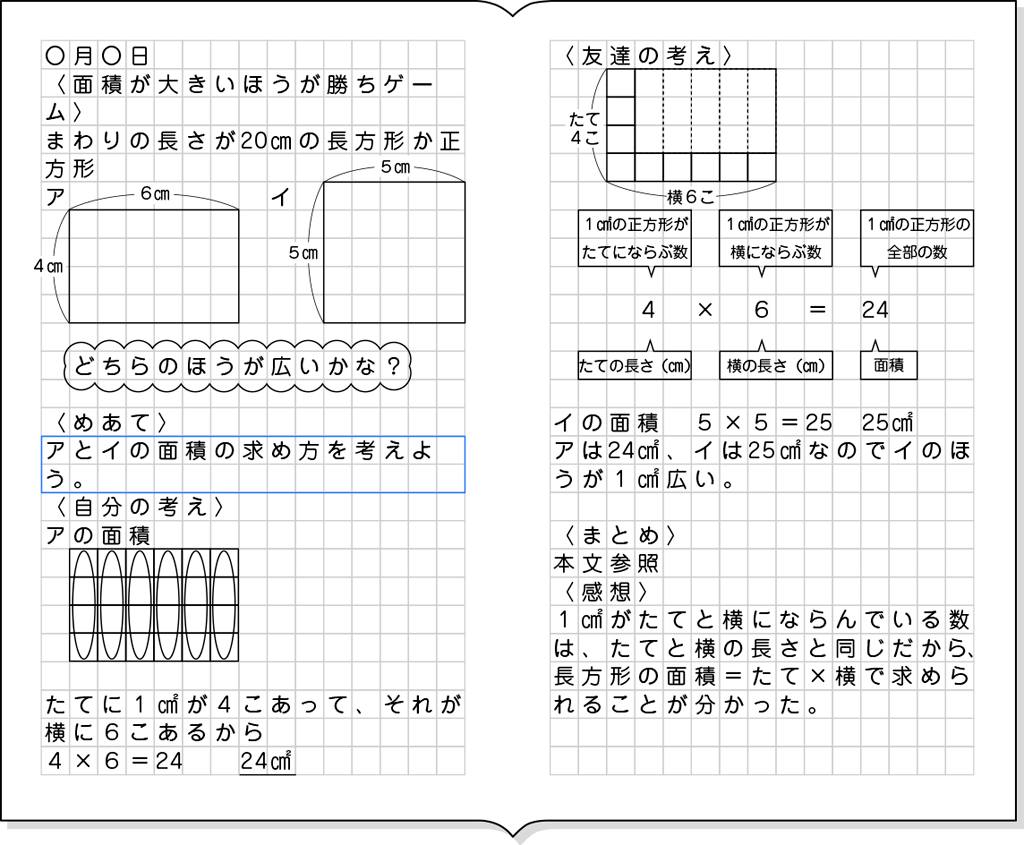
｢面積が大きいほうが勝ちゲーム」をしましょう。ルールを説明します。周りの長さが20㎝になる長方形か正方形をノートにかきます。面積が一番大きい長方形か正方形をかいた人が勝ちです。

周りの長さが20㎝になるということは、縦と横の長さを足したら、10㎝になる長方形か正方形をかけばいいね。赤＋赤＋青＋青＝20㎝だから、赤＋青は20㎝の半分になるね。

細長い長方形もできますね。

全部で５通りかくことができたけれど、どれが一番面積が大きい図形かな。

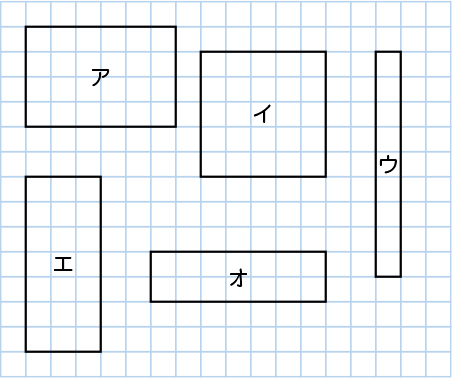
アとウの長方形だと、アの長方形のほうが面積が大きいと思います。

みんながつくった長方形、正方形のなかで、一番面積が大きい図形はどれでしょう。

※一番面積が大きいと思うものを予想させる。

私はアだと思います。

イも広そうだよ。

アとイだと、どちらのほうが広いのかな。

アとイの面積を求めることはできますか。

前の時間に学習した１㎠の正方形の何個分か考えればいいと思います。

１㎠の正方形の数を数えるのは大変だな。

面積を計算で求めることはできないかな。

では、面積を計算で求める方法を考えてみましょう。

アとイの面積の求め方を考えよう。

見通し

１㎠の正方形を縦と横に何個並べることができるかな。

アの長方形は、縦に１㎠の正方形を並べると、４個並べることができます。

自力解決の様子

※ノートに長方形の図をかかせて、どのように考えたか説明も書くように伝えます。

Ａ　つまずいている子
１㎠のマスをかいて数えている。

Ｂ　素朴に解いている子
１㎠のマスをかいて、その数の求め方をかけ算を用いて説明している。

Ｃ　ねらい通り解いている子
長方形の面積の求め方を考え、１㎠の正方形が縦に４個並べることができ、それが６個あることから、かけ算を用いて１㎠がいくつ分かを縦と横の長さを用いて考え、説明している。

学び合いの計画

実際に方眼のマス目のあるノートに縦４㎝、横６㎝の長方形をかかせて、１㎠が24個あることから、面積は24㎠であることを全員で確認します。そして、数えなくても面積が24㎠であることを、縦に1㎠の正方形が並ぶ数と、それがいくつ分あるかを考えることで、かけ算を用いて面積を求めることができることを理解させていきます。

本時では、長方形や正方形の面積を求める際、単位となる正方形を敷き詰めるのではなく、計算によって面積を求める方法について考えることができるようにすることが大切です。その際、正方形や長方形では、辺にそって１辺が１㎝の単位正方形を規則正しく並べることができることから、乗法を用いると、その個数を手際よく求めることができるよさに気付き、計算を用いて面積を求めたり、｢長方形の面積＝縦×横（または横×縦）」という公式を見いだしたりしていきます。

４×６の４は、長さの４ではなく、１㎠の正方形が縦に４個並んでいるので、正方形が４個分の４であること、横の６も、６㎝ではなく、１㎠の正方形が横に６個並んでいるので６個分であることの６であること、つまり、長さ×長さをしているのではなく、結果的に１㎠の正方形の並ぶ個数と長さが等しいため、１㎠の正方形の個数をかけ算を用いて求める際、縦の長さと横の長さを用いることで、１㎠の正方形の個数が分かります。

子供たちのなかには、長さと長さをかけ算していると考えている子もいると思いますが、面積は単位正方形の何個分かで求めることができることを繰り返し扱っていくことで、公式の意味理解にもつながっていきます。公式を形式的に覚えさせるのではなく、公式を導いた根拠も説明できるようにしていくことが大切です。

ノート例

Ｂ　素朴に解いている子

単位正方形の並び方に着目し、縦に４個並んでいるまとまりが横に６個あることから、乗法の式を用いて面積を求めることができていたら、計算によって面積を求められることを理解していると考えることができます。

Ａ　つまずいている子　

単位正方形を敷き詰めてその数を数えればよいことは理解できている場合、単位正方形の数を計算で求めることはできないか、これまでの既習事項を思い出させるよう声かけをしましょう。縦に４個並んだまとまりがいくつ並んでいるか考えさせることで、乗法の式で求められること、また、縦に並んでいる単位正方形の数は縦の長さの数値と同じであり、同様に横に並んでいる単位正方形の数は横の長さの数値と同じであることに全体で確認していくことで、長さと長さを掛けているのではないことに気付かせていくことも大切です。