小３算数「あまりのあるわり算」指導アイデア《問題に応じた商の処理の仕方》

特集: 文部科学省教科調査官監修｢教科指導のヒントとアイデア｣

2024.10.29

単元の展開

第１・２時　割り切れない場合の計算の仕方（包含除）14÷３
▼
第３時　割り切れない場合の計算の仕方（等分除）16÷３
▼
第４時　割り切れない場合の答えの確かめ方
▼
第５時（本時）問題に応じた商の処理の仕方（余りを考える問題）
▼
第６時　まとめ

本時のねらい

商や余りの意味に着目して、問題に応じた商の処理の仕方を考え、説明することができる。

評価規準

商や余りの意味に着目して、図などを用いて問題に応じた答えの求め方を考え、説明している。

本時の展開

ケーキが23こあります。１箱に４こずつ入れていきます。ケーキを全部入れるには何箱ひつようですか。

どんな式になりそうですか。

23÷４です。

どうしてわり算なのですか。

同じ数ずつ、ケーキを分けていくからです。

そうですね。同じ数に分けていくことを「わり算」で表すことができるのでしたね。答えはどうなりますか。

５余り３です。５箱に入れて３つ余ります。だから、５箱必要です。

でも、よく問題を見ると、ケーキを全部入れないといけないよ。

そうか。余りの３つも箱に入れないといけないんじゃないかな。

つまり、６箱必要だ。

なるほど。余った３個も箱に入れないといけないんですね。今までの問題とどんなことが違いますか。

計算の答えをそのまま使うと、問題の答えに合わないところです。

余ったケーキも箱に入れないといけないところです。

余りをどうするかを考えなくてはいけないのですね。では、次の問題ではどうでしょう。

１台の車にタイヤを４こ使って、おもちゃの車を作ります。タイヤは30こあります。何台の車が作れますか？

これもわり算の問題だから、式は30÷４です。

割り切れないから、余りが出るね。

今回の問題も余りが出てきそうですね。今日は余りに注目して問題を考えていきましょう。余りをどうするか考えて、答えを求めましょう。また、わけも考えましょう。

余りをどうすればよいか考えよう。

見通し

問題①と同じように、余りがあるので１足して考えればいいんじゃないかな。

図を使って考えればはっきり分かるよ。

かけ算を使ってわけを考えてみよう。

自力解決の様子

A　つまずいている子
式は書けているものの、余りの処理の仕方が分からず、そのまま「７台余り２個」や前問と同様に考え、答えを＋１して「８台」と回答している。

Ｂ　素朴に解いている子
計算の答えが「７余り２」であることから、答えも「７台」と書いている。

Ｃ　ねらい通り解いている子
Ｂの子に加えて、「余り２ではタイヤが足りずに作れないから、この問題は＋１をしない」と前問と比べて説明することができている。

学び合いの計画　

この単元では、既習事項（わり算）を活用しながら、余りのあるわり算について考えていく単元です。本時での子供がつまずく場面として、余りの捉え方と処理が考えられます。立式することや計算の答えを求めることは可能ですが、問題場面の答えとして余りをどう処理していくかに難しさがあります。そのため、日常場面に即しながら考察したり、具体物や図を活用しながら問題場面を視覚的に表したりすることでより良い理解につながります。

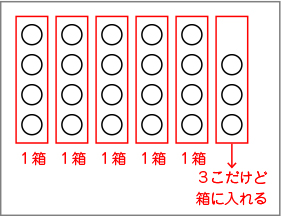
例えば、問題場面①ではケーキを４個ずつ入れていくと５箱はきれいに入れることができますが、３個余ってしまった場面を「答え５箱」とするのではなく、余ってしまった３個も箱に詰めないといけないことを確かめたり、図のように表し、すべて箱に入れるためにはもう１つ箱を用意しなければならないことが視覚的に理解したりできるように工夫します。

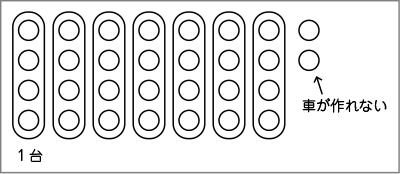
また、問題場面②では、タイヤが４個ずつ７台分と余り２個の場面では、タイヤ２個では車を作ることができないから、余りのタイヤは使わないことを理解させます。そのため、自力解決の際は、図やブロックを使って考えている子供に対し、｢なるほど。図があると分かりやすいね」｢ブロック使っているから説明が上手だね」と称賛し価値付けていくことが大切になります。その際、問題場面①のケーキの問題と比較させ、｢余りの分を考えて、計算の答えに１を足すときと足さないときがある」と気付けるようにします。

練り上げの際は、どうして車の問題では答えに１を足さないのか、どんなときに１を足すのかと、余りの処理の仕方について話合いを行い、余りの処理の仕方について日常場面に即して考察し、理解を深めるようにすることが大切です。適用発展の際に、子供自ら問題を作成し、子供どうしで問題を出し合う活動も考えられます。余りの処理を考える問題をつくり、ICTを活用しながら全体に共有することで、今日の学びを深めていく活動につながります。