小４算数「わり算２けた」指導アイデア《３位数÷２位数＝２位数の筆算》

特集: 文部科学省教科調査官監修｢教科指導のヒントとアイデア｣

2024.10.29

単元の展開

第１時　数の構成に着目し、「何十で割る計算」の仕方を考える。
▼
第２時　「２位数÷２位数（仮商修正なし、余りなし）」の筆算の仕方を考え理解する。
▼
第３時　「２位数÷２位数（仮商修正なし、余りあり）」の筆算の仕方を考え理解する。また、「割る数×商＋余り＝割られる数」の関係と検算の仕方を理解する。
▼
第４時　「２位数÷２位数」の筆算で、過大商を立てたときの仮商修正の仕方を考え、その計算をする。
▼
第５時　「２位数÷２位数」の筆算で、仮小商を立てたときの仮商修正の仕方を考え、その計算をする。
▼
第６時　「２位数÷２位数」の筆算で、除数の切り捨てや切り上げを選んで仮商を立てて計算する。
▼
第７時　「２位数÷２位数」の筆算を基に「３位数÷２位数＝１位数」の筆算の仕方を考え、その計算をする。
▼
第８時（本時）「３位数÷２位数＝２位数」の筆算の仕方を考え、その計算をする。
▼
第９時　「３位数÷２位数＝２位数」の筆算で、除数の切り捨てや切り上げを選んで仮商を立てて計算する。
▼
第10時　商に０が立つ場合の簡便な筆算の仕方や「３位数÷３位数」の筆算の仕方を考え、その計算をする。
▼
第11時　除法について成り立つ性質を考え、理解する。
▼
第12時　末尾に０のある数の除法の簡便な筆算の仕方と余りの求め方を考え、その計算をする。
▼
第13時　学習内容を適用して問題を解決する。
▼
第14時　割られる数や割る数の一部が分かっていない場合のわり算の筆算（虫食い算）について、筆算の仕組みを考えながら解決する。

本時のねらい

｢３位数÷２位数＝２位数」の筆算の仕方を考え、その計算をすることができる。

評価規準

既習の除法の筆算の仕方を基に、345÷21などの商を十の位に立てる計算の仕方を図や式を用いて考え、説明している。（思考・判断・表現）

本時の展開

※色紙を提示する。

色紙が345枚あります。この色紙を21人で同じ数ずつ分けると、１人分は何枚になって何枚余りますか。

わり算で答えを求められるぞ。

式は345÷21です。

筆算で計算できそうだ。

数が大きいからできるかな。

では、今日は345÷21の筆算の仕方を考えましょう。

※出題後、すぐに式を立てたり筆算をしたりする子供もいますが、ここでは筆算の最初の部分を書いて手が止まっている子供を確認しておきます。そして、計算の仕方を考えるという学習のねらいを共有します。

345÷21の筆算の仕方を考えよう。

見通し

①結果の見通し

だいたい何枚くらいになりそうですか。

〈Ｃ１〉１人分が10枚だとすると、10×21＝210だから、10枚より多そう。

②方法の見通し

どのように筆算しますか。

〈Ｃ２〉今までと同じように「立てる」｢掛ける」｢引く」｢下ろす」の順に計算します。

〈Ｃ３〉一の位に数を立てます。

〈Ｃ４〉これまでは商は一の位に立てていたけれど、十の位から立てられるかもしれません。

※Ｃ１、Ｃ３、Ｃ４は十進位取り記数法に基付いた数の見方につながり、Ｃ２は類推的な考え方につながります。このような発言や式を板書し、この後に考える筆算の仕方のヒントにつなげます。

自力解決の様子

Ａ　つまずいている子
・商が何の位に立つか分からず手が止まっている。

何の位から商を立てればいいのかな？

Ｂ　素朴に解いている子
・一の位に商を立てて計算している（もしくは途中で止めている）。

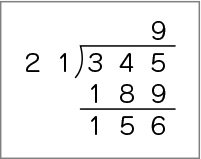
できたぞ。でも、あまりが大きすぎるような……。

・商を「10」と立てて計算している（もしくは途中で止めている。）

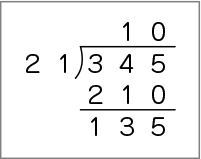
余ったのを21でもう一度割ってみよう。

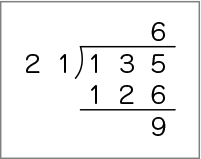
Ｃ　ねらい通り解いている子
・商を十の位に立て、既習の手順で計算している。

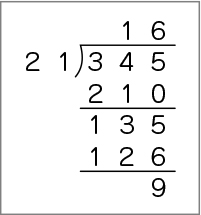
計算できました！

学び合いの計画

最初の自力解決では、Ａ～Ｃの子供のように商が立てられない子供から、既習の除法の計算の仕方を基に計算できる子供まで存在します。自力解決では、このような子供たちを教師が見とり、把握することが大切です。そして、机間巡視で教師が手を止めている子供に対して「何が分からないのか（できないのか）？」｢おかしいな（変だな）と思うことは何か？」などと問いかけることによって、ＡやＢのような子供の問いを引き出します。

一方、Ｃのような既習の手順で計算している子供には、形式的に計算できていることは把握できますが、計算過程の意味を理解しているかどうかはまだ分かりません。そこでＣのような子供には、計算過程について具体的な場面（345枚の折り紙を21人で分ける）と関連付けた説明を考えさせます。

説明し合う場面では、まずＡの子供のような「何の位に商は立つのか」という問いを共有し、問題を焦点化して考えます。そして、筆算の過程と具体的物の操作の過程を関連付けながら考えることによって、筆算の計算過程や数の意味を理解させていきます。ここで重要なことは「まず折り紙を10の束で１束ずつ21人に分ける」という操作が、｢十の位に商１を立てて21に掛ける」ということにつながることと、210枚分けた後に残った135枚を１のばらで６枚ずつ21人に分ける」という操作が、｢一の位に商６を立てて、21に掛ける」ということにつながるということです。このようなことを全体で説明し合う場面で注目させます。

全体で説明し合った後はペアやトリオになり、一方が操作し、もう一方がその手順に合わせて筆算を書いて計算する活動（もしくは一方が筆算を書いて、もう一方がその手順に合わせて操作をする活動）を行います。こうすることで、子供一人一人に考えさせることができるとともに、教師は子供の様相を形成的に評価し、指導していくことができます。

※デジタル教材がある場合は、タブレットPＣ上で操作させたり筆算を書かせたりするとよいです。