小４算数「垂直平行四辺形」指導アイデア《平行四辺形の作図の仕方》

特集: 文部科学省教科調査官監修｢教科指導のヒントとアイデア｣

2024.10.23

単元の展開

第１時　２本の直線の交わり方を調べる活動を通して、垂直の意味を知り、垂直な２直線を弁別する。
▼
第２時　三角定規を使って、垂直な直線の引き方を理解する。
▼
第３時　２本の直線の並び方を調べる活動を通して、平行の意味を知り、平行な２直線を弁別する。
▼
第４時　平行な直線は他の直線と等しい角度で交わることや、平行な直線の間の距離は一定であることを理解する。
▼
第５時　三角定規を使って、平行な直線の引き方を理解する。
▼
第６時　方眼上の直線の垂直や平行の関係を理解する。
▼
第７時　辺の並び方に着目して、台形と平行四辺形の特徴を理解する。
▼
第８時　平行四辺形の性質について、辺の長さや角の大きさを調べたことを基に説明する。
▼
第９時（本時）平行四辺形の辺の位置関係や構成要素を基に、平行四辺形の作図の仕方を理解する。
▼
第10時　ひし形の辺の位置関係や構成要素を基に、ひし形の特徴を調べ、作図の仕方を理解する。
▼
第11時　作図した四角形を弁別する活動を通して、様々な四角形の特徴を捉え直す。
▼
第12時　対角線の意味と、様々な四角形の対角線の特徴を理解する。

本時のねらい

平行四辺形の辺の位置関係や構成要素を基に、平行四辺形をかくことができる。

評価規準

平行四辺形の辺の位置関係や、長さ、角の大きさを使って、平行四辺形のかき方を考えている。

本時の展開

※はじめに下のような図を提示し、本時の問題を伝えた後、図アのような教師が意図的に誤って作図した四角形を提示します。

下のような平行四辺形のかき方を考えましょう。

今日はこのような平行四辺形のかき方を考えます。先生は、はじめに辺ＢＣをかき、次に辺ＡＢをかきました。先生がかいた平行四辺形を見てください。

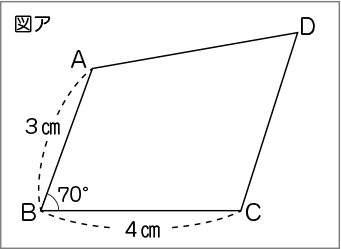
※教師がかいた図は、拡大図ではなく実寸でかいた図形を画面に提示するとよいです。

あれ？　先生がかいた四角形は平行四辺形になっていません。

先生がかいた四角形のどこを見て、平行四辺形ではないと言っているのですか。

向かい合っている辺が平行になっていません。

向かい合っている辺の長さも等しくなっていないと思います。

四角形の辺の長さや角の大きさ、向かい合う辺の並び方に着目し、教師がかいた四角形が平行四辺形でないと感じる根拠を説明する子供の発言を、全体で共有します。子供が前時までに学習した、｢向かい合った２組の辺がそれぞれ平行になっている」｢向かい合った辺の長さが等しい」｢向かい合った角の大きさが等しい」という平行四辺形の定義と性質を基に、平行四辺形を考えるようにします。

教師がかいた四角形を全員に配付し、子供たちが言ったことを確認させます。ここで、｢辺ＡＤと辺ＢＣ、辺ＡＢと辺ＤＣが平行になっているか」「辺ＡＤと辺ＢＣ、辺ＡＢと辺ＤＣが同じ長さになっているか」を調べることは、平行四辺形の作図をする場合と同じ操作になります。図イ、図ウのように四角形を修正して平行四辺形にする子供がいた場合は、その子供の図を写真に撮るなどして全体で共有するとよいです。

このような導入を行うことで、多くの子供が平行四辺形の作図の仕方について見通しをもつことができます。辺の長さを調べる際に、ものさしで長さを測る子供が多いと予想されますが、図イのようにコンパスを使う方法を確認し、作図に生かせるようにするとよいです。

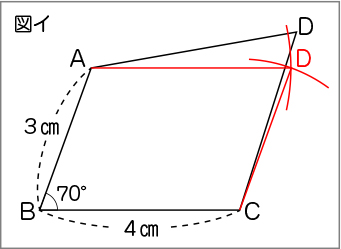
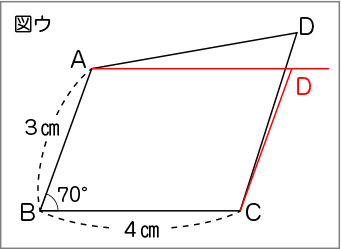
平行四辺形について学習したことを使って、平行四辺形のかき方を考えよう。

自力解決の様子

※自力解決の際、はじめに辺ＢＣをかき、次に辺ＡＢをかくことは共通で行うと、作図の仕方が共有しやすくなります。

Ａ　つまずいている子
ノートのマス目を利用して平行四辺形をかいていて、辺の長さ、角の大きさ、辺の位置関係といった平行四辺形の定義や性質を使っていないため、正しく平行四辺形をかけていない。

Ｂ　素朴に解いている子
辺ＢＣに平行な４㎝の辺ＡＤをかき、分度器で70°を測って平行四辺形を完成させている。

Ｃ　ねらい通り解いている子

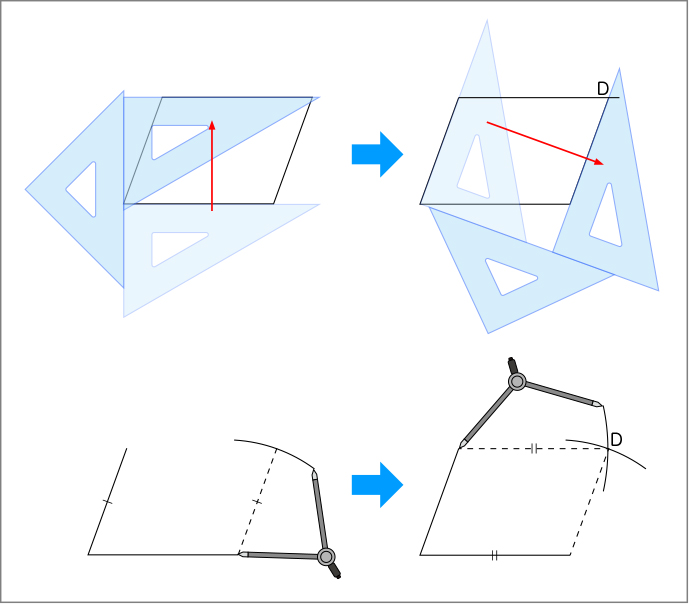
学び合いの計画

授業支援アプリを活用して、それぞれの子供がかいた平行四辺形の写真を提出させ、子供の解決の様子を把握します。ほとんどの子供が自力で平行四辺形をかくことができていれば、全員の考えを全体で共有し、その図を用いてペアや小グループでかき方を説明する時間を設けます。

その際、教師は自力解決でつまずいていた子供のそばに行き、学び合いの様子を見守り、必要ならば個別に支援をします。自力で平行四辺形をかくことができない子供が多かった場合や、子供の作図の方法が偏っていた場合には、全体でかき方を検討します。その際、友達がかいた図を見て、自分が考えなかった方法について考えることができるよう、発言する子供を意図的に指名するとよいです。

ノート例

Ｂ　素朴に解いている子

Ａ　つまずいている子　

全体発表とそれぞれの考えの関連付け

・頂点Ａ、頂点Ｃからそれぞれ、辺ＢＣ、辺ＡＢと平行な直線を引き、２つの直線が交わったところが頂点Ｄになる。

・頂点Ａ、頂点Ｃからそれぞれ辺ＢＣ、辺ＡＢと同じ長さのところに印をつけ、２つの印が交わったところが頂点Ｄになる。

平行四辺形のかき方を共有する際には、その手順だけでなく、上の２点のような頂点Ｄの位置がどのように決まったかをきちんと確認します。

学習のまとめ

並行四辺形のかき方が共有された後は、｢○○さんのような方法で平行四辺形をかくことができるのはなぜでしょう」｢○○さんはどうしてその方法で平行四辺形をかくことができると考えたのでしょう」などと問い、子供が平行四辺形をかく方法を、｢向かい合った２組の辺がそれぞれ平行になっている」｢向かい合った辺の長さが等しい」｢向かい合った角の大きさが等しい」という平行四辺形の定義や性質を関連付けて考えるようにし、本時のまとめとましょう。