小6算数「分数÷分数」指導アイデア《分数の乗法や除法を適用する問題で、演算決定をし、問題解決する》
執筆/富山大学教育学部附属小学校教諭・羽柴直子
監修/文部科学省教科調査官・笠井健一、前・富山県南砺市立福光東部小学校校長・中川愼一

目次
単元の展開
第1時 除数の分子が1のときの分数÷分数の式の意味と、計算の仕方を考える。
▼ 《除数の分子が1のときの分数÷分数の計算》
第2時 分数÷分数の計算の仕方を考える。
▼ 《割る数の分子が1でないときの計算》
第3時 除数が仮分数の計算の意味を理解する。
▼
第4時 帯分数で割る計算の仕方を考える。
▼
第5時 帯分数での除法の文章題を、線分図や表を基に解く。
▼
第6時 被除数、除数、商の関係を調べる。
▼
第7時(本時)分数の乗法や除法を適用する問題で、演算決定をし、問題解決することができる。
▼
第8時 既習事項の確かめをする。
本時のねらい
比較量や基準量が分数の場合でも、倍を表す数は除法で求められることを図や式を用いて考えることができる。
評価規準
整数や小数で成り立つ考え方を基にして、倍を表す数は除法で求められることを図や式を用いて多面的に捉え、考えている。(思考・判断・表現)
本時の展開
※問題①の学習は、学級の子供たちの実態に応じて取り入れるようにするとよいでしょう。

ピンク、黄、青の3本のリボンがあります。ピンク、黄のリボンの長さは、青のリボンの長さの何倍ですか? 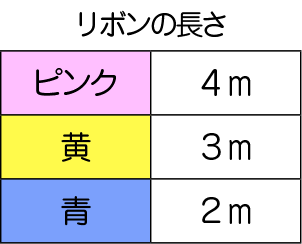
ピンクのリボンの長さ4mは、青のリボンの長さ2mの何倍ですか。
2倍です。
どうしてすぐに2倍と分かるのですか。
4mは2mの2つ分だからです。
それを式に表すとどうなりますか。
「2+2=4」です。
「2×2=4」でもよいです。
なるほど。2mが2つとか、2mの2倍ということが式から読み取れますね。ただ、この場面は2倍ということを求める場面ですね。何倍なのかを□を使って式にすると、どうなりますか。
「2×□=4」です。
□を求める式にすると、「4÷2=□」です。
それを言葉の式に表すと、どうなりますか。
「ピンクのリボン÷青のリボン=2倍」です。
黄のリボンの長さは青のリボンの長さのだいたい何倍ですか。
1倍の2mよりも長くて、2倍のピンクのリボンの4mより短いので、1倍と少しです。
1倍と2倍の真ん中だから、1.5倍です。
黄のリボンの長さは青のリボンの長さの何倍かは、どうやったら分かりますか。
何倍かを求めるときは、青のリボンの長さを基にして、そのいくつ分かを考えればいいです。
基にする数が2なのだから、3を2で割る計算をします。
「3÷2」です。
比べる数の3を、基にする数の2で割ります。
それを言葉の式にすると、どうなりますか。
「黄のリボン÷青のリボン=割合」です。
公式で言うと、「比べられる量÷基にする量=割合」です。
基にする量が青のリボンだということは、どこに目を付けたら分かるのですか。
「青のリボンの長さの何倍ですか」という文から分かります。
とくに目を付けたのは、その文のなかのどの部分ですか。
「青のリボンの長さの」の「の」の部分です。
「○○の」と出てきたら、基にする量なのですか。
だいたいそうです。「△△は」なら、比べられる量です。
困っているみなさんは、今の説明で納得できましたか。
まだ、十分に納得できるほどではないのですが、「青いリボンの長さ2m」が基にする量だということは、なんとなく分かりました。
「比べられる量÷基にする量=割合」に数を当てはめて、「3÷2」では何倍になりますか。
1.5倍です。
何が何の1.5倍なのですか。
黄のリボンの長さが青のリボンの長さの1.5倍です。
他のみなさんも、「黄のリボンの長さが青のリボンの長さの1.5倍」ということでよいですか。
よいです。(多数)
3mは2mの1.5倍です。
図にかくと分かりやすくなると思います。
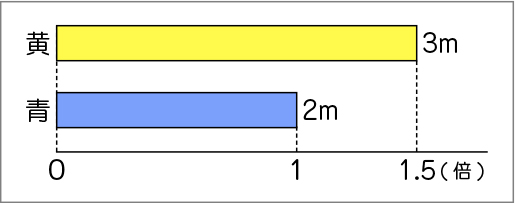
本当だ。黄のリボンと青のリボンの関係が、目で見て捉えられます。
黄のリボンと青のリボンの関係そのものを図に表したら、次のようになります。
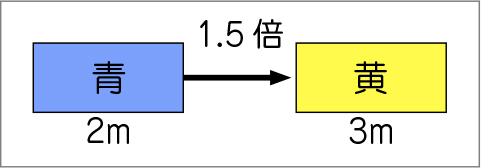
「黄のリボンの長さが青のリボンの長さの1.5倍」ということがよく分かります。
1.5倍のことを1[MATH]\(\frac{1}{2}\)[/MATH]倍とも言えるし、[MATH]\(\frac{3}{2}\)[/MATH]倍とも言えます。
1.5倍 や1[MATH]\(\frac{1}{2}\)[/MATH]倍という見方は、2つ分や3つ分という見方とどう違うのですか。
2つ分、3つ分というのは、ちょうど割り切れて整数倍になるときだけ使える見方です。いつでも割り切れるわけではないので、「倍の見方」を使っていくことが大事です。
みなさん、それでよいですか。
※ほぼ全員が挙手する。
ここでの学びで確かめることができたことは何ですか。
倍を求めるわり算は、「比べる量÷基にする量」だということです。
倍には、「整数」だけでなく、「小数」や「分数」にもなるということです。
他のみなさんも、今の話のように、「わり算の意味」や「倍の意味」について考えを確かめることができましたか。
はい。確かめることができました。(多数)

赤、青、白の3本のリボンがあります。赤、青のリボンの長さは、白のリボンの長さのそれぞれ何倍ですか?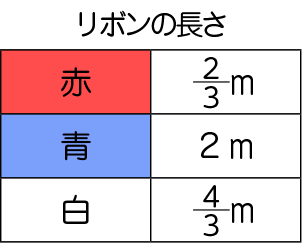
問題①の場面の学びを使って、赤、青のリボンは、それぞれ白のリボンの何倍になるかを考えることができそうですか。
できそうですが、基にする量が分数なので、どうしようかなと思っています。
分数だと長さがどれくらいなのかひと目で分からないので、自信がありません。
赤、青、白と3つあるので、どれを基にするのかが分かりにくいです。
みなさんが困っていることを解決するために、まず何をすればよいですか。
基にする量が何かをはっきりさせれば、いいと思います。
基にする量は何ですか。
「白のリボンの長さ[MATH]\(\frac{4}{3}\)[/MATH]m」です。
白いリボンが基にする量だということは、どこに目を付けたら分かるのでしたか。
「白いリボンの長さの何倍ですか」という文です。
「白いリボンの長さの」の「の」の部分です。
みなさんは、今の説明で納得できそうですか。
「白のリボンの長さ[MATH]\(\frac{4}{3}\)[/MATH]m」を基にする量にすることは、頭ではなんとなく分かります。
頭だけでなく、心から納得するためには何が必要ですか。
さっきのように図に表したらいいと思っています。
同じように、図があったら、納得を深めることができそうだと思っている人は、手を挙げてみてください。
※多数が挙手する。
それでは、黒板に図をかくことを手伝えそうな人は前に出てきてください。
※子供と一緒に、黒板にテープ図を作成する。
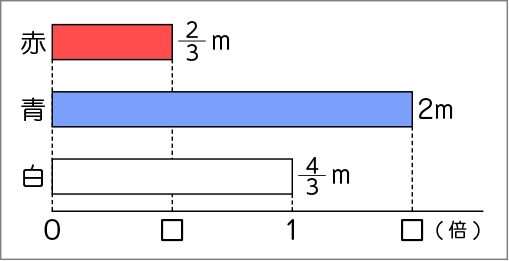
どうですか。リボンの長さの関係をつかむことができそうですか。
白いリボンを基にすることが分かってきました。
白いリボンを基にするということは、白いリボンの長さを1と見るということです。
わり算にするときに、白のリボンの長さの[MATH]\(\frac{4}{3}\)[/MATH](m)で割ればいいのだと思います。
関係の図にも表してみたいです。
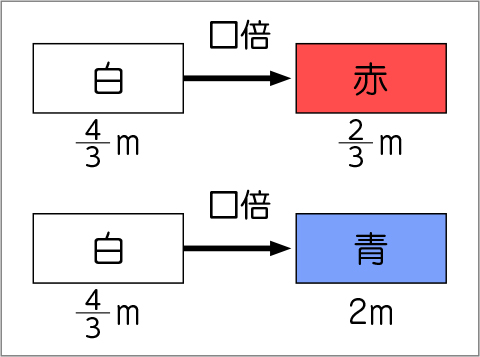
みなさん、白いリボンを基にする量として、その何倍かを考えていくということに納得できましたか。「基にする量」の次に、解決したいと思っていることは何ですか。
割る数が [MATH]\(\frac{4}{3}\)[/MATH]という分数だということです。
割る数が分数だと、どんな困ることがあるのですか。
計算が難しいことです。
倍の意味が分かりにくいことです。
それではみんなで、基にする数が分数のときにわり算を使って何倍かを求めていくことについて考えていきましょう。

基にする数が分数のとき、わり算を使って何倍かを求めることについて考えよう。
見通し
何倍になるかを図や数直線図から見当を付けて考えよう。(方法の見通し)
整数倍や小数倍と同じように、わり算を使って分数倍も求めることができるのかを考えよう。(方法の見通し)
比べられる数を基にする数で割ると、何倍になるのか分かるので計算しよう。(結果の見通し)
自力解決の様子
A つまずいている子
何倍かを求める計算がわり算だということがよく分からない。
- 何倍を求める学習をしたことはある。
- 問題を解決するときに、乗法や除法のどちらを使うのかがよく分からない。
- どの数とどの数を掛けたり割ったりするのかがよく分からず、当てずっぽうに組み合わせてしまう。
- 自信をもって計算できない。
- 図や数直線を使うことが難しく、分数の倍をイメージすることができない。
B 素朴に解いている子
分数倍のイメージを十分にもてていない。
- 何倍を求めるときには、基にする数のいくつ分と考えて、わり算で計算することは理解している。
- 本単元で学んだ分数のわり算の計算方法で答えを求めることができる。
- 分数の答えを導くことはできるが、分数倍の意味はイメージできていない。
C ねらい通り解いている子
倍を求めるわり算や分数倍について理解している。
- 図や数直線を用いて、問題解決をするために、乗法と除法のどちらを適用すればよいのかを理解している。
- 分数倍を求めるときには、除法を使うことを、図や数直線で表しながら説明しようとしている。
- 整数倍や小数倍のように倍について、「1と見たときに〇に当たる」と分数でも表せることを統合的に捉えている。
学び合いの計画
本時は、分数のわり算を用いて、比較量や基準量が分数で表された場合の割合を求める場面です。割合に関する学習については、第3学年では、「2の□倍が6」といった整数の範囲について、第1用法、第2用法、第3用法にふれてきています。
第4学年では、「10の□倍が12」といった割合を表す数が小数になる場合について学習してきています。第5学年では、小数の場合の3つの用法について学習しました。そのため、第1用法、第2用法、第3用法を分数の範囲に広げて学習する第6学年の本単元の問題に対しても、公式「比べる量÷基にする量」に数を当てはめて答えを出すだけで満足してしまう子供も少なくはありません。
本単元では、整数倍や小数倍のように、倍について「1と見たときに〇に当たる」と分数でも表せることを統合的に捉え、図を用いて考えを説明することを大切にします。子供にとって、分数倍をイメージすることは容易ではありません。そこで、自力解決や全体発表において、関係図や数直線テープ図を用いて可視化し、説明する手立てが大切になってきます。
【割合の3用法】
割合の3用法というのは、割合に関する3つの計算方法をまとめて言い表したものです。
(第1用法) p=A÷B
割合の第1用法は、2つの量A、Bが分かっているとき、AがBの何倍に当たるか。すなわち、Bを基にしたときのAの大きさの割合pを求める方法です。

(第2用法) A=B×p
割合の第2用法は、基にする量(B)と割合(p)が分かっていて、比べる量(A)を求める方法です。
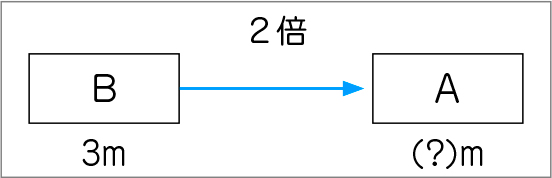
(第3用法) B=A÷p
割合の第3用法は、比べる量(A)と割合(p)が分かっていて、基にする量(B)を求める方法です。
ノート例
A つまずいている子
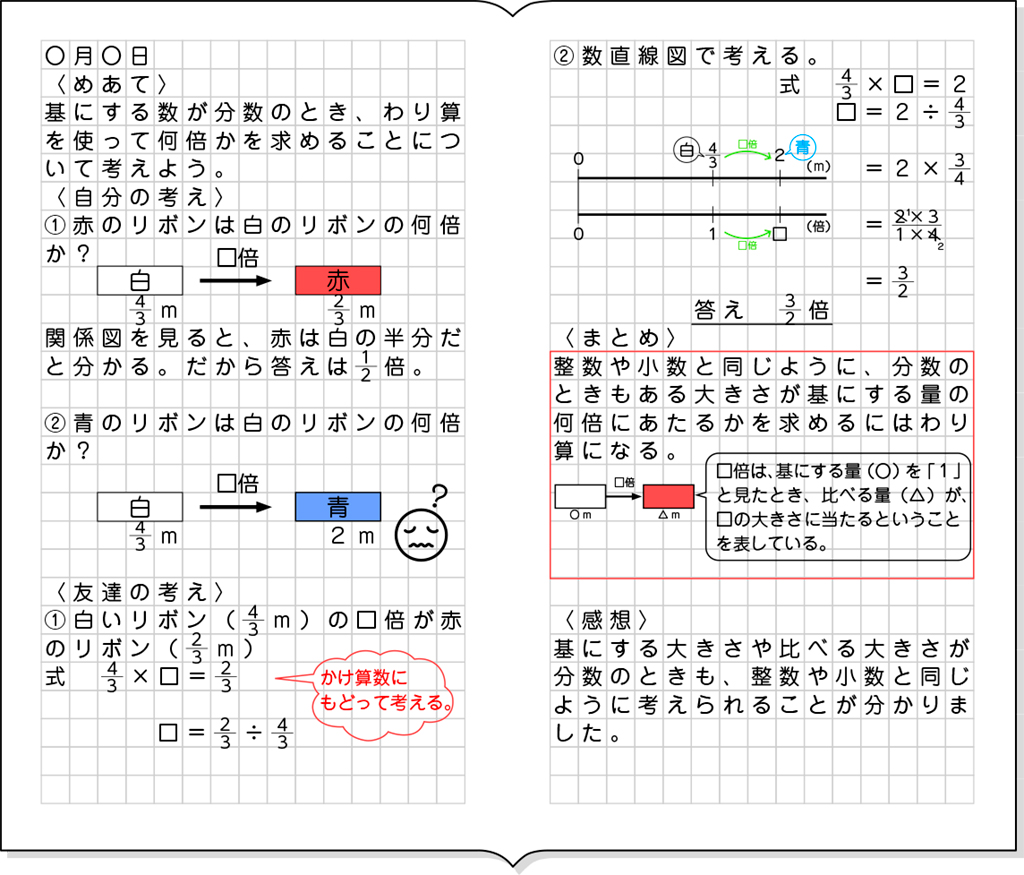
B 素朴に解いている子

全体発表とそれぞれの考えの関連付け
赤、青のリボンの長さは、白のリボンの長さのそれぞれ何倍か、求めることはできましたか。
イラスト/横井智美

