小６算数「文字を使った式」指導アイデア《場面や図と式を結び付けて、式を読み取る》

特集: 1人1台端末時代の｢教科指導のヒントとアイデア｣

2024.07.30

単元の展開

第１時　ｘやaなどの文字を使った式の表し方を知る。
▼
第２時　文字に数を代入して、式の値を求める。
▼
第３時　乗法の場面を文字式で表し、文字に当てはまる数の求め方を考える。
▼
第４時　加法の場面を文字式で表し、文字に当てはまる数の求め方を考える。
▼
第５時　乗法や加法の混じった場面を文字式で表し、文字に当てはまる数の求め方を考える。
▼　　　《乗法や加法の混じった場合を文字式で表す》
第６時（本時）場面や図と式を結び付けて、式を読み取る。
▼
第７時　文字式に様々な数を当てはめ、図形と式を結び付けて、式が表す意味を考える。
▼　　　《文字式が表す意味》
第８時　既習事項の確かめをする。

本時のねらい

問題の場面や図と結び付けて、ｘ・ｙを用いて式に表し、その式の意味について考える。

評価規準

問題場面の数量の関係に着目し、ｘ・ｙを用いて式に表したり、その式の意味を考えたりしている。（思考･判断･表現）

本時の展開

次の場面を式に表して考えましょう。
①40円のチョコレートとｘ円のジュースを買います。代金はｙ円です。
②面積が40㎠の平行四辺形があって、底辺の長さはｘ㎝です。高さはｙ㎝です。

今から、①の場面を紹介します。｢40円のチョコレートとｘ円のジュースを買います。代金はｙ円です｣。この場面を表す式は、次の4つのうち、どの式だと思いますか？

（Ａ）40＋ｘ＝ｙ　
（Ｂ）40－ｘ＝ｙ　
（Ｃ）40×ｘ＝ｙ　　
（Ｄ）40÷ｘ＝ｙ

（Ａ）だと思う人｡（Ｂ）だと思う人｡（Ｃ）だと思う人｡（Ｄ）だと思う人。

※（Ａ）から（Ｄ）まで順に挙手させていく。

みんなが（Ａ）に手を挙げていたけれど、どうして､（Ａ）だと思ったのですか。（一人一人に理由を答えさせていく）

40円のチョコレートとｘ円のジュースの２つを合わせたものがｙ円です。図で表すと次のようになります。（黒板に線分図をかいて説明する）

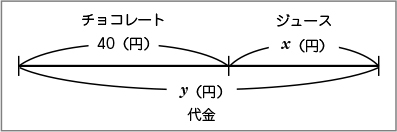
だから、チョコレートの値段とジュースの値段をたし算で表した（Ａ）が正しいと思います。

そう！　そう！

図を使うと、ｘとｙの関係が分かりやすくて説得力があるよね。

ｘやｙなどの文字で表された場面を式に表すと、どのようになるのかをもう少し考えていきましょう。では、②の場面はどうでしょう。｢面積が40㎠の平行四辺形があって、底辺の長さはｘ㎝です。高さはｙ㎝です｣。この場面を表す式は次の４つのうち、どの式だと思いますか。

（Ａ）40 ＋ｘ＝ｙ
（Ｂ）40 －ｘ＝ｙ
（Ｃ）40 × ｘ＝ｙ
（Ｄ）40 ÷ ｘ＝ｙ

平行四辺形の公式はかけ算だから、Ｃじゃないかな。

でも、この場面に合わせると、違ってくるかもしれない……。

場面に合う式はどれだろう。

式だけを見ていると、ｘが何でｙが何だったのか分からなくなるね。

ｘとｙが何なのかをはっきりさせて考えていく必要がありそうだよ。

ｘとｙが何を表しているのかはっきりさせて、場面に合う式を考えよう

見通し

ｘとｙが何を表しているのか、場面をしっかり読み取ればよさそうだ。（方法の見通し）

平行四辺形の公式に当てはめた式になりそうだ。（結果の大きさの見通しなど）

自力解決の様子

A　つまずいている子
（Ｃ）40×ｘ＝ｙ
・平行四辺形の面積の公式「平行四辺形の面積＝底辺×高さ」から、かけ算だと思い込み、｢（Ｃ）40×ｘ＝ｙ」を選んでいる。

Ｂ　素朴に解いている子
（Ｄ）40÷ｘ＝ｙ
・平行四辺形の面積の公式「平行四辺形の面積＝底辺×高さ」にｘとｙを当てはめて、｢40＝ｘ×ｙ」を見いだしている。
・｢40＝ｘ×ｙ」を変形させると、｢（Ｄ）40÷ｘ＝ｙ」になることに気付いている。
・底辺の長さがx㎝、高さがy㎝の平行四辺形の図をかき、その面積を40㎠と表して、40÷ｘ＝ｙの式になる平行四辺形は何通りもあることに気付いている。

Ｃ　ねらい通り解いている子
（Ｄ）40÷ｘ＝ｙ
・ｘが底辺、ｙが高さ、40が面積であることを整理して、平行四辺形の面積の公式「平行四辺形の面積＝底辺×高さ」に照らして、40＝ｘ×ｙを見いだしている。
・「40＝ｘ×ｙ」を変形させると、｢（D）40÷ｘ＝ｙ」になることに気付いている。
・底辺の長さがｘ㎝、高さがｙ㎝の平行四辺形の図をかき、その面積を40㎠と表して、40÷ｘ＝ｙの式になる平行四辺形は何通りもあることに気付いている。
・ｘとｙの関係について考えて、ｘとｙの関係は積が一定の関係であり、ｘが大きくなればなるほど、ｙが小さくなることに気付いている。
・40÷ｘ＝ｙのｘとｙには、整数だけでなく、小数や分数も当てはめることができることについて考えている。

学び合いの計画

多くの子供は、平行四辺形の面積の公式「平行四辺形の面積＝底辺×高さ」を想起し、この公式に「40」｢ｘ」｢ｙ」を当てはめようと解決の見通しをするでしょう。しかし、場面の読み取りが不十分な子は、かけ算だと思い込み、｢（Ｃ）40×ｘ＝ｙ」を選んでしまいがちです。

そこで、なぜ「（Ｃ）40×ｘ＝ｙ」にならないのか、子供一人一人が納得することができるように、平行四辺形の図を用いて「40」｢ｘ」｢ｙ」がそれぞれ何を表しているのか確かめたり、言葉で考えを表現したりするようにしましょう。さらに、１人で考えるだけでなく、ペアの友達と考えを聞き合ったり、２人で考えを深め合ったりする場を設けましょう。自分の考えを友達に聞いてもらい、｢なるほど、分かった！」など納得してもらうことで、子供は自分の考えに自信をもつことができます。また、２人で話し合うことによって、考えの修正点を見付けたり、新たな気付きを生み出したりします。

学び合いでは、図・式・言葉を関連付けて、式の意味を確認し、学級全員で学び合う意識を大切にしながら展開していきましょう。

ノート例

Ａ　つまずいている子

Ｂ　素朴に解いている子

全体発表とそれぞれの考えの関連付け

｢面積が40㎠の平行四辺形があって、底辺の長さはｘ㎝です。高さはｙ㎝です｣。この場面を表す式は、どの式だと思いますか。

｢（Ｃ）40×ｘ＝ｙ」だと思います。平行四辺形の面積の公式「平行四辺形の面積＝底辺×高さ」だから、かけ算なので（Ｃ）だと思います。

僕と同じ考えだ。賛成です。

私は、違う考えです。｢（Ｄ）40÷ｘ＝ｙ」だと思います。

〈○○さん〉どうして、わり算なの！？

面積の公式はかけ算なのに、わり算の式を選んだことに驚いているんですね。○○さんと同じように、平行四辺形の面積の公式なのに、わり算の式の「（Ｄ）40÷ｘ＝ｙ」を選ぶのはおかしい、間違っていると思った人はいますか(挙手を求める)。間違っているとまでは思わないけれど、｢（Ｄ）40÷ｘ＝ｙ」を選ぶ理由を説明しようとすると、ちょっと自信がないという人はどのくらいいますか（挙手を求める）。

どうしてわり算を選んだのか、そのわけを聞きたいです。

（Ｄ）を選んだ友達に理由を聞かせてほしいのですね。では、｢（Ｄ）40÷ｘ＝ｙ」を選んだみなさんのなかで、その理由を説明できそうな人はいますか（挙手を求める）。十分な説明とまではいかないけれど､（Ｄ）を選んだ理由を自分なりに考えてみたら、こんなことかもしれないということなら話せそうだという人もいるのではないですか（挙手を求める）。それでは､（Ｃ）ではなく（Ｄ）を選んだ自分なりの理由を話してみてください。

〈◎◎さん〉平行四辺形の面積の公式「平行四辺形の面積＝底辺×高さ」に、｢40」｢ｘ」｢ｙ」を当てはめると、｢40＝ｘ×ｙ」になります。この「40＝ｘ×ｙ」を変形させると、｢40÷ｘ＝ｙ」になるので､（Ｄ）だと思いました。

私も◎◎さんの考えに似ています。この場面を平行四辺形の図に表すと、このようになります（ICT機器で表現した図を提示する）。底辺の長さがｘ㎝、高さがｙ㎝で、その面積が40㎠となるので、式は「ｘ×ｙ＝40」となります。この式を変形させると、｢（D）40÷ｘ＝ｙ」になります。

なるほど。図に表すと、場面が想像できて、分かりやすかったよ。

みなさんは、この考えに納得できましたか。

〈▲▲さん〉みんながわり算と言うから、そうなんだろうなと思うようになってきました。でも、ｘとｙがどんな数なのか分からないので、本当に納得するというまでにはなっていません。

　▲▲さんが納得できるようにするためには、どうしたらよいと思いますか。

ｘとｙと分からないものが２つあるから考えにくいのだと思います。底辺の長さｘに、仮の数を入れて考えたらいいと思います。

例えば、底辺の長さが10cmなら、10×ｙ＝40です。そうすると、40÷10＝ｙがこの場面を表していることが正しいと分かると思います。

〈▲▲さん〉そうか。だから「（Ｄ）40÷ｘ＝ｙ」をみんなは選んだんだね。少し分かってきました。

式の全体だけでなく、それぞれの数が何を表しているのかを考えることが大切ですね。

今の考えを聞きながら気付いたんだけど、平行四辺形の面積の公式だと考えると、ｘとｙにはいろいろな数が入るんだなと、あらためて思いました。

そうだとみんなは思いますか。例えば、ｘ＝４、ｘ＝５だったらどうですか。

ｘ＝４の場合……、ｙ＝40÷４＝10。ｘ＝５の場合……、ｙ＝40÷５＝８になります。

あれ。ｘが大きくなればなるほど、ｙが小さくなっているよ。

ｘとｙの関係を表に表すと、こんな感じになったよ。

※表で表した子供の考えを提示する。

「40÷ｘ＝ｙ」から「ｘ×ｙ＝40」ということは、底辺のｘに高さのｙを掛けた、その面積はいつでも40ということだから、底辺の長さのｘが大きくなればなるほど、高さのｙが小さくなるんだね。

ｙが分数になることが、なんだかすっきりしない感じがします。どれくらいの大きさかも分からないし……。

[MATH]\(\frac{40}{３}\)[/MATH]を 13[MATH]\(\frac{１}{３}\)[/MATH]とすれば、どれくらいの大きさは分かるようになるよ。

小数に直して、13.33……としたらどうかな。

13.33×３＝39.99です。39.99……と９が続いて、限りなく40に近付くことは分かるけど、ｘとｙを掛けたら40になる関係を表しているというには少しだけ無理があるように感じます。

この場合は分数のほうがよさそうだけれど、ｙが小数や分数になる場合もあるということですか。

例えば、40÷16＝2.5という計算が成り立つので、ｘが16のとき、ｙは2.5になるよ。

他にも、あるのかな。

ｘが32のとき、ｙは1.25になるよ。

ｘが80のとき、ｙは0.5だよ。

いろんな場合があるということは、ｙだけでなく、ｘも整数の他に小数や分数でもできるんじゃないかな。

｢40÷ｘ＝ｙ」や「ｘ×ｙ＝40」という式の意味を考えていくなかで、ｘやｙにどんな数でも入りそうだということに気付いたんですね。

ｘ、ｙは整数じゃなくても、小数や分数でもできます。

ｘが１より小さくても、ｙが40より大きくなるだけなので、どんな数字でも入ります。

｢40÷ｘ＝ｙ」や「ｘ×ｙ＝40」という式のｘやｙに、どんな数でも入るということを平行四辺形に戻して考えたら、どんなことが言えるのですか。

平行四辺形の面積の公式には、どんな数も入るということです。

｢40÷ｘ＝ｙ」や「ｘ×ｙ＝40」という式で表すことのできる平行四辺形の底辺の長さや高さは何通りもあるということです。

学習のまとめ

評価問題

数量の関係が次の①～③の式で表される場面を、下のア～ウから選んで、記号で答えましょう。
①16＋ｘ＝ｙ
②16－ｘ＝ｙ　
③16×ｘ＝ｙ

ア　縦が16㎝、横がｘ㎝の長方形があります。面積はｙ㎠です。
イ　16ｇの袋にｘｇの荷物を入れたら、全体の重さはｙｇになりました。
ウ　16Ｌの水をｘ人で分けます。1人分はｙＬになります。
エ　公園で16人遊んでいましたが、ｘ人帰りました。残ったのはｙ人です。

子供に期待する解答の具体例

①イ　②エ　③ア

本時の評価規準を達成した子供の具体の姿

問題場面の数量の関係に着目し、ｘ・ｙを用いて式に表したり、その式の意味を考えたりしている。

感想例

平行四辺形の公式「底辺×高さ＝平行四辺形の面積」に当てはめて、平行四辺形を想像して考えると、当てはまる場合の式40÷ｘ＝ｙを見付けることができました。
○や△と同じように、x や y などの文字を使って式に表せばよいんだなと考えました。
x や yにはいろんな数が入るけれど、その数の範囲はどこからどこまでかを考えておく必要があると考えています。
最初はかけ算だと思っていたけれど、図をかいたら納得できました。場面を想像できるようにするために、図や表はすごく役立つなと思いました。
分からない数がある場合でも、文字を使うと式に表せます。だから、文字は便利だと思いました。
これからも文字を使った式を正しくうまく使っていきたいと思いました。
これからも、文字を使った式の意味を考えるときは、図や表を使って、場面を想像して考えたいと思いました。
40×ｘ＝ｙとなる場面は、｢底辺が40㎝、高さがｘ㎝の平行四辺形の面積はｙ㎠です」｢40ｍのｘ倍は、ｙｍです」｢40円のガムをｘ個買うと、代金はｙ円です」など、何通りもあることに気が付きました。式というのは、とてもシンプルに数量の関係を表しているからこそ、数値の関係をひと目で捉えることができるんだなと思いました。