小4算数「わり算1けた」指導アイデア《何十(何百)÷1桁の除法(あまりなし)の計算の仕方を説明する》

執筆/東京都目黒区立駒場小学校主任教諭・越後真紀
監修/文部科学省教科調査官・笠井健一、東京学芸大学玉川大学非常勤講師・長谷豊

目次
単元の展開
第1時 (本時)あまりのない、何十や何百のわり算(60÷3、600÷3)や、各位とも割り切れるあまりのない2位数÷1位数(63÷3など)の計算の仕方を説明する。
▼
第2時 あまりのない2位数÷1位数(72÷3など)の計算の仕方を、既習の計算を基にして説明する。
▼
第3時 あまりのない2位数÷1位数(72÷3など)の筆算の仕方を理解する。
▼
第4時 各位とも割り切れず、あまりのある2位数÷1位数(93÷4など)の筆算の仕方を説明する。
▼
第5時 十の位が割り切れる、あまりのある2位数÷1位数(83÷4など)の筆算の仕方を説明する。
▼
第6時 各位とも割り切れない3位数÷1位数=3位数(472÷3など)の筆算の仕方を、既習のわり算の計算の仕方を基に説明する。
▼
第7時 商に空位を含み、割り切れる3位数÷1位数=3位数(642÷6など)の筆算の仕方を説明する。
▼
第8時 首位に商が立たない3位数÷1位数 (252÷6など)の筆算の仕方を説明する。
▼
第9時 2位数÷1位数=2位数の暗算と、商が何十、何百何十になる3位数÷1位数の暗算の仕方を考える。
▼
第10時 他国のわり算の筆算の仕方を知り、自国のわり算の筆算の仕方と比べ、共通点や相違点を見いだす。
▼
第11時 問題に取り組み、学習内容の定着を確認し、理解を確実にする。
本時のねらい
10や100のまとまりを用いて、乗法九九1回の適用で商が求められる何十(何百)÷1桁の除法(あまりなし)の計算の仕方を考え、説明することができる。
評価規準
何十(何百)÷1桁の除法(乗法九九1回適用・あまりなし)の計算の仕方を考え、10や100のまとまりを用いて説明している。(思考・判断・表現)
本時の展開

□まいの色紙を3人で同じ数ずつ分けます。 1人分は何まいになりますか。
今日は、この問題を解きたいと思います。
このままでは、答えが出せません。
そうですね。このままでは式も立てられませんね。
式にはできます。
えっ。できるのですか。では、ノートに書いてみてください。
□÷3です。
本当ですか。
色紙が何枚かあって、それを3人で同じ数ずつ分けるということは、トランプ配りの場面と一緒です。こういう場面はわり算で表せると3年生のときに勉強しました。
付け足しです。例えば、□が12だったら、12枚の色紙を3人で同じ数ずつ分けるのだから、12÷3=4で、1人分は4枚になります。
なるほど。「例えば」というのがいいですね。□にどんな数を入れても、この場面は□÷3でいいですか。
□の数によってはあまりが出るときもあるけど、式は□÷3です。
確かに。数によっては割り切れない場合もありますよね。ところでさっき、12枚の色紙を3人で同じ数ずつ分ける場合は12÷3というのは、みなさんは納得ですか。では、1人分が4枚になるのは、どうやって分かったのですか。
3の段の九九で、12になるのは4だからです。
12÷3=○で、○を求める場合は、3×○=12と考えて、○に当てはまる数が答えです。
なるほど。かけ算九九を使えば答えが導けるのでしたね。では、実際に数を変えて考えてみましょう。18枚だったらどうですか。
18÷3です。
3×6が18になるので、答えは1人分が6枚です。
すごいですね! かけ算九九で答えが出るんですね。では、27枚だったらどうですか。
27÷3です。
3×9=27なので、答えは1人分が9枚です。
かけ算九九はすばらしいですね。一発で答えが出てくるのですね。では、60枚だったらどうですか。
60÷3だけど……。
3×□=60になる九九はありません。
3の段の九九の最高はさっきの3×9=27ですね。27より大きくなったら、かけ算九九は使えないのでしょうか。

60÷3の計算の仕方を考えよう。
見通し
27枚より大きい数のわり算の計算の仕方を考えましょう。
掛ける数が1大きくなると答えは3ずつ大きくなるのだから、10、11、12……と順に大きくしていって、答えに3を足していけばいいんじゃないかな。
確かにできるけど、大変だね。
60が6だったらできるんだけどな。
なるほど。確かに60を6と見ることができたら6÷3=2と考えられますね。なんとかして、60を6と見る方法がないでしょうか。
あ、分かった。できるかも。
自力解決の様子
A つまずいている子
・形式的に60÷3を行っている。
60÷3の60から0をとって6÷3=2。さっきとった0を付けて答えは20。
B 素朴に解いている子
・図を使って説明している。
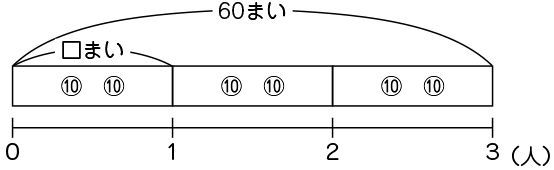
C ねらい通り解いている子
・10の束で考える。
60は10の束で考えると6÷3=2で1人2束。10枚が2束で20枚。
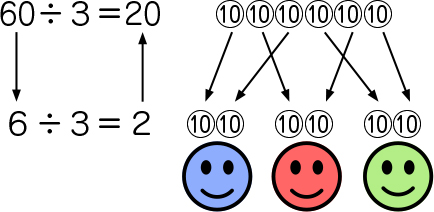
学び合いの計画
イラスト/横井智美

