小６算数「算数のまとめ」指導アイデア《算数のクイズ（仕事算）に取り組む》

特集: 1人1台端末時代の｢教科指導のヒントとアイデア｣

2024.04.23

単元の展開

第１時　中学校の数学の問題（０より小さい数）に取り組む。
▼
第２時　中学校の数学の問題（図形の性質を利用した作図など）に取り組む。
▼
第３時　ほかの国の算数について調べたり、問題に取り組んだりする。
▼
第４時　和算について調べたり、和算の問題に取り組んだりする。
▼
第５時（本時）算数のクイズ（仕事算）に取り組む。
▼
第６時　算数のクイズ（面積図など）に取り組む。
▼
第７時　算数のパズル（魔方陣など）に取り組む。

本時のねらい

単位量当たりの大きさや割合の学習を基にして、仕事算の解き方を考える。

評価規準

｢全体を１と見る考え」などを活用して、仕事算を解決することができる。（思考・判断・表現）

本時の展開

イベントのお知らせの紙をふうとうに入れるために紙を４等分に折ります。
・Ａさんが１人でこの作業をすると12分間かかります。

問題場面が想像できますか。(紙を４つに折る様子を見せる）

紙を折るのに12分もかかるの？

イベントだから案内の紙がたくさんあるのだと思います。

この場面には続きがあります。

イベントのお知らせの紙をふうとうに入れるために紙を４等分に折ります。
・Ａさんが１人でこの作業をすると12分間かかります。
・Ｂさんが１人でこの作業をすると８分間かかります。

ＡさんとＢさんの作業の進み具合についてどんなことが分かりますか。

Ｂさんのほうがかかっている時間が少ないです。

Ｂさんのほうが折るスピードが速いと思います。

Ａさんのほうが折るスピードが遅いと思います。

なるほど。Ａさんは紙をていねいに折っているのかもしれませんね。さらに続きがあります。

イベントのお知らせの紙をふうとうに入れるために紙を４等分に折ります。
・Ａさんが１人でこの作業をすると12分間かかります。
・Ｂさんが１人でこの作業をすると８分間かかります。
・ＡさんとＢさんがいっしょにこの作業をすると、何分間かかるでしょう。

ＡさんとＢさんの２人で一緒に作業をすると、どのくらいの時間がかかると思いますか。

平均すると10分です。だから、10分かかると思います。

でも、Ａさん１人でも12分でできるんだから、２人だったらもっと早くできるはずです。

じゃあ、半分の５分ぐらいかな。

平均の考えを使って考えていますね｡（平均の考えでは正答を得られないが、子供から提案されたら、ここでは認めておきます）

５分かもしれないけど、このままでは分からないと思います。

どういうことですか。

紙が何枚あるかが分からないからです。紙がたくさんあると時間が余計にかかるかもしれません。紙が何枚あるか分かれば２人の作業の速さを求めることができると思います。

確かに紙の枚数が分からないと考えにくいですね。何枚だと思いますか。

※子供が、100枚、200枚などと言う。

では、紙の枚数が120枚あって、２人で作業をした場合を考えてみましょう。

２人で作業をしたときにかかる時間について考えよう。

本時では、仕事算を扱います。中学校の入試問題の準備を経験していない子供には、｢ある仕事をＡさんが１人ですると……」などと言っても、その場面をイメージしにくいと思われます。仕事という言葉から、この授業で扱う場面がイメージしにくいかもしれないので、ここでは紙を折るという場面を用い、｢仕事」の代わりに「作業」という言葉を使っています。

仕事算の解法では、仕事全体の量を１と見るという方法がよく使われます。本時では、この考えを天下り的に与えるのではなく、紙の枚数が公倍数の場合を考えさせます。複数の事例を扱うことで、紙の枚数が異なる場合も、２人のそれぞれの作業の時間が決まれば、｢２人で作業をしたときにかかる時間が変わらないこと」を理解させていきます。

単位量当たりの大きさや割合の学習を想起させることで、紙の枚数すなわち仕事全体の量を１と見るという発想につなげていきます。

自力解決の様子

A　つまずいている子
・120枚という情報をどのように問題解決に使うか分からない。
・Ａ、Ｂの１分間当たりの枚数を求めるが、次に進めない。
Ａ　120÷12＝10　１分で10枚折れる。
Ｂ　120÷８＝15　１分で15枚折れる。

Ｂ　素朴に解いている子
Ａ　120÷12＝10　１分で10枚折れる。
Ｂ　120÷８＝15　１分で15枚折れる。
Ａ、Ｂの２人だと１分で25枚折れる。
120÷25＝4.8　２人だと4.8分かかる。

Ｃ　ねらい通り解いている子
・紙の枚数（仕事全体の量）を１と見て、２人で作業したときの時間を求めている。
紙の枚数を１と見ると
Ａ　１÷12＝[MATH]\(\frac{1}{12}\)[/MATH]
Ａは１分で全体の1/12の作業ができる。
Ｂ　１÷８＝[MATH]\(\frac{1}{8}\)[/MATH]
Ｂは１分で全体の[MATH]\(\frac{1}{8}\)[/MATH]の作業ができる。
Ａ、Ｂの２人だと、[MATH]\(\frac{1}{8}\)[/MATH]＋[MATH]\(\frac{1}{12}\)[/MATH]＝[MATH]\(\frac{5}{24}\)[/MATH]で、１分で全体の[MATH]\(\frac{5}{24}\)[/MATH]の作業ができる。
だから、1÷[MATH]\(\frac{5}{24}\)[/MATH]＝[MATH]\(\frac{24}{5}\)[/MATH]＝4.8　２人だと4.8分かかる。

この問題の解き方を知らない子供に対して、自力解決の際にヒントカードなどでＣまで高めることまでをめざすのではなく、全体交流で仕事全体の量を１と見る発想を理解させることをめざします。

｢Ａ　つまずいている子供」に対しては、ＡさんやＢさんが１分間でそれぞれ何枚折れるかを考えるよう促します。Ａさんを例として、12分で120枚折れることから、１分で何枚折れるか考えるよう促します。次のような線分図などを使うことも考えられます。

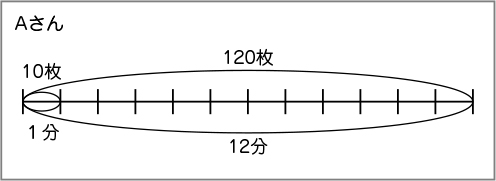
Ａさんを手がかりに、Ｂさんの場合について考えるよう促します。また、ＡさんとＢさんが１分間で折れる枚数を求めることができても、そこで行き詰まっている子供に対しては、２人で一緒に作業をすると１分間で何枚折れるかを確認し、全体の120枚を折るのに何分間かかるかを考えるよう促します。

全体交流では、２人の折る枚数を合わせた枚数を線分図を使ってイメージをもたせつつ、比例関係を押さえながら、｢時間」が「折る枚数」÷「１分間で折ることのできる枚数」で求められることを式表現なども使いながら確認していきます。

学び合いの計画

学び合いは以下のように進めるように計画します。
①　紙が120枚の場合について考え方と答えを確認する。
②　①をふまえて、紙の枚数が12と８の公倍数の場合について、２人の作業の時間を求める。
③　仕事の全体量を「１」と見たときについて考える。
上でも述べたように、③を天下り的に指導するのではなく、｢単位量当たりの大きさ」の学習を想起させ、紙の枚数を１として考えてみることへとつなげていきます。

ノート例

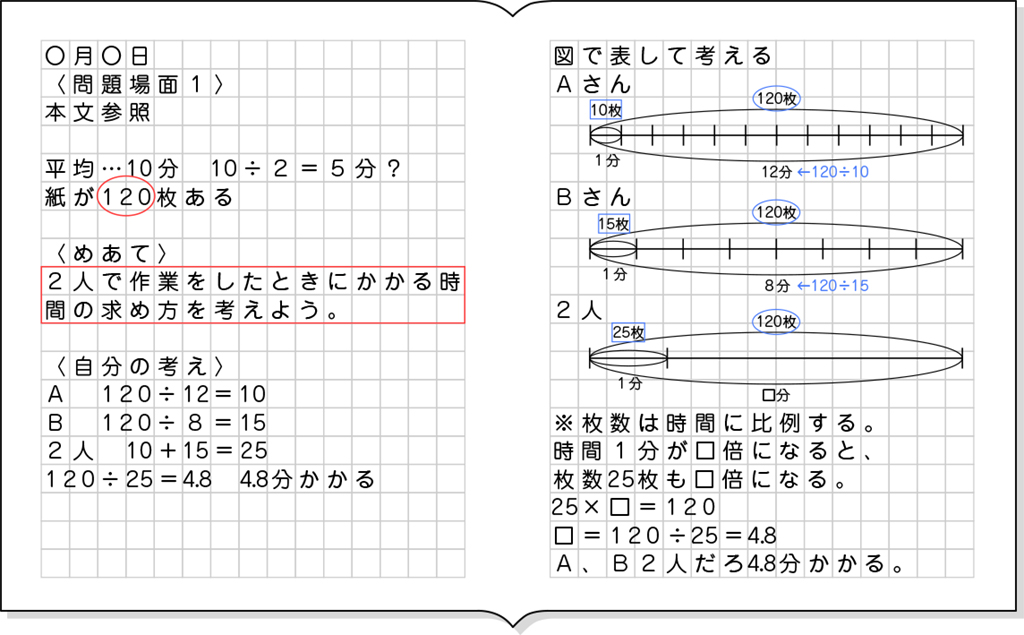
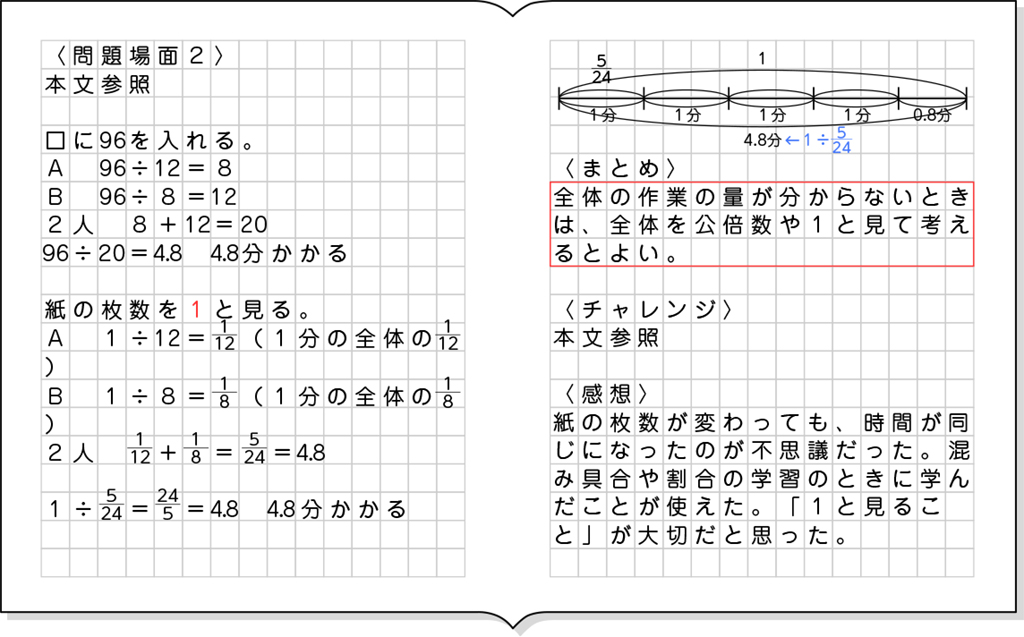
全体発表とそれぞれの考えの関連付け

まず、ＡさんとＢさんが１人で作業したときに、１分で何枚折れるか教えてください。

Ａさんは１分で10枚、Ｂさんは１分で15枚折ることできます。

その10は、どのようにして見付けましたか。（ほかの子供に答えさせてもよい）

120÷12を計算しました、

確かに120÷12は10ですね。でも、どうして120÷12をしたのですか。

Ａさんは12分で120枚折れます。だから、1分で折れる枚数は120を12で割ればよいです。

なるほど。これまで算数の勉強で、比例について学習してきました。比例という言葉を使って、12で割るわけを説明できますか。

枚数は折る時間に比例します。時間が12分から１分に[MATH]\(\frac{1}{12}\)[/MATH]になると、枚数も[MATH]\(\frac{1}{12}\)[/MATH]になります。[MATH]\(\frac{1}{12}\)[/MATH]を求めるためには、12で割ればよいです。

どちらも枚数が時間に比例していることを基にして、120÷12であることが説明できていますね。今言ってくれたことを図で表すこともできます。いろいろな図が考えられますが、今日は線分図を使ってみます。例えば、Ａさんについて、次のような図をかいてみます。

※線分図のすべてを最初から提示するのではなく、線分を書いた後、｢全体が120枚あること」｢全部を折るのに12分かかっていること」｢１分は12等分に当たること」｢１分では120÷12＝10（枚）折れること」を、子供と一緒に確認します。

（図を適宜を指さしながら）この図からも、時間が枚数に比例していることが読み取れますね。

※Ｂさんが１人で１分で折ることのできる枚数も同じように確認します。

次に、ＡさんとＢさんが一緒に作業をする場合を考えます。ＡさんとＢさんが一緒に作業すると、１分間で何枚折れますか。

１分間でＡさんが10枚、Ｂさんが15枚折れるから、10＋15で25枚だと思います。

そうですね。２人で協力して仕事が早くなったりすることもあるかもしれませんが、ここでは、そのようなことは起こらなくて、１分で25枚折れるとしましょう。このことを、線分図で表してみましょう。

では、Ａ、Ｂ２人では、何分かかるでしょうか。どのような計算になるか、隣どうしで話し合って考えてみましょう。

※時間をとる。

何分かかるか求めるために、どのような計算をしますか。

120を25で割ればよいと思います。

図で説明できますか。

例えば、Ａさんの図では、120枚を10枚で割ると120÷10で、全部折るのに12分かかることが分かります。同じように、２人のときは、120枚を25枚で割ればよいと思います｡（注：｢枚数」÷「枚数」という説明になっている）

なるほど。計算としては確かに120÷10＝12（120、10、12を指示棒などで指しながら確認する）です。この120枚や10枚が何を表しているか、もう少しくわしく説明できる人はいますか。

120枚は紙全部の枚数です。10枚はＡさんが１分間で折れる枚数です。全体の枚数120を１分間で折れる枚数10枚で割ると、何分で折れるか出ると思います。

ただの10枚ではなく、「１分間で10枚折れること」が大切ですね。では、Ｂさんのほうも同じことが言えるか、説明できる人はいますか。

Ｂさんも、全体の枚数の120枚を１分間で折れる８枚で割ると、120÷８＝15になって、15分で全部折れると思います。

なるほど。同じように考えると、Ａ、Ｂ２人の場合も、全体の120枚を「２人が１分間で折れる25枚」で割れば求められるということですね。もう１つ質問があります。Ａ、Ｂ２人の図では、１分、□分、25枚、120枚という４つの数量があります。さっき話に出た比例という言葉を使って、この場面を言えますか。

よく分かりません。

Ａのほうは１分、12分、10枚、120枚の４つの数量があります。これだったら、比例という言葉を使って関係を言えませんか。

時間が１分から12分に12倍になっているから、枚数も10枚から120枚の10倍になっています。

そうです。Ｂさんも言えますね。では、同じように、Ａさん、Ｂさん２人の場合も言えますか。□があるので難しいですが、同じように言える人はいませんか。

時間が１分から□分に……。

この場合、何倍になっていると言えますか。

□倍です。時間が１分から□分に□倍になっていれば、枚数も□倍です。

だいたいよいですね。枚数について、何の□倍がいくつになっているか、きちんと言えますか。

　25枚の□倍が120枚になっています。

素晴らしい。これを式で表すとどうなりますか。

25×□＝120です。

そうです。では、□を求めるためには、どのような計算をしますか。

120を25で割ればよいと思います。

そうですね。いろいろ考えると、□は120÷25で求められることが分かりました。□はいくつになりますか。

計算すると、4.8になります。

4.8分？

4.8分は少し違和感があるかもしれません。分数を使うと、0.8＝[MATH]\(\frac{4}{5}\)[/MATH]、[MATH]\(\frac{4}{5}\)[/MATH]は[MATH]\(\frac{48}{60}\)[/MATH]です。[MATH]\(\frac{48}{60}\)[/MATH]分は[MATH]\(\frac{1}{60}\)[/MATH]分の48個分。つまり１秒の48個分なので48秒と言えます。今日は、秒に直さずに、4.8分でよいことにしておきましょう。

最初に平均で考えた人がいましたが、平均の半分になら……なかったですね。平均を使うという発想はよかったと思います。今日は、平均で答えが出ない場合もあるということが勉強になりましたね。では、この考えを使って、次の問題を考えてもらいます。

イベントのお知らせの紙が□枚あります。この紙をふうとうに入れるために紙を４等分に折ります。
・Ａさんが１人でこの作業をすると12分間かかります。
・Ｂさんが１人でこの作業をすると８分間かかります。
・ＡさんとＢさんがいっしょにこの作業をすると、何分間かかるでしょう。

問題場面１と２で同じことや違うことが分かりますか。少し考えてみてください。

※少し時間をおく。

まず、同じことを聞きましょう。

紙を折るところが同じです。

ＡさんとＢさんの作業の時間も同じです。

どちらも２人で作業したときの時間を求める問題です。

なるほど。２つの場面はよく似ていますね。では、次に、違うことを教えてください。

紙の枚数が□になっています。

そうですね。実は、□には、みなさんに数を選んで入れてもらおうと思います。さっきは120でした。みなさんなら□をいくつにしますか。実は、□をいくつにするかで、問題の計算が易しくなったり、難しくなったりします。計算を易しくするためにはいくつを入れたらよいか、問題場面１の解き方をふり返って考えてみましょう。

※120÷12＝10、120÷８＝15、10＋15＝25、120÷25＝4.8という計算をしたことをふり返る。

実は、先生は計算ができるだけ楽になるように120を選びました。どうして120を選んだか分かりますか。

12や８で割り切れるようにしていると思います。

そうですね。最初のわり算が割り切れないと計算が大変になりそうですね。では、どんな数だとよさそうですか。

12と８の公倍数がよいと思います。

そうですね。では、□をいくつにしましょうか。

24がいいと思います。

ほかにもあります。48、72、96のどれかがいいと思います。

では、今出た数のどれかを選んで、問題場面２の問題を解いてみましょう。まず、自分で解いて、その後、隣どうしで説明し合いましょう。

※96と72を取り上げて、式を板書する。

ＡさんとＢさんの作業の時間がすべて同じで、紙の枚数が120、96、72の場合の結果が出ました。みなさん、気付いたことがありますね。

どれも、4.8分になっています。

そうですね。授業の最初に紙の枚数が分からないからできないという意見がありましたが、今のところ、同じ結果になっているということですね。ところで、今日は１分間当たり何枚折れるかということを考えてきました。この１分間当たり何枚ということを算数でしっかり学習した学年があります。５年生のときですが、覚えていますか。

※以下のやりとりについて、子供がこちらの意図通りの反応が出ない場合は、無理に引き出さず、適宜教師が話してもよい。

覚えていません。

単位量当たりの大きさです。

よく覚えていましたね。混み具合などを勉強しましたね（ICTで５年生の教科書を見せる）。このときも公倍数を使って、畳の枚数をそろえて混み具合を比べましたね。実は、割合の学習でも公倍数を使って考えました（ICTで５年生の教科書を見せる）。

バスケットのシュートの記録

ＡチームとＣチームのどちらがうまいかを調べるときに、シュートした回数を公倍数でそろえて比べた人もいたかもしれませんね。ところで、公倍数でそろえて比べる方法は分かりやすいけど、実は困ることがあるのです。どんなことだと思いますか。

比べる人が２人ではなくて、３人や４人になると、公倍数を求めるのが大変そうです。

その通りです。だから、単位量当たりの大きさや割合を考えるのですね。ところで、上のＡさんのシュートの例では、シュートした回数を基にすると、入った回数の割合は[MATH]\(\frac{3}{8}\)[/MATH]になります。このとき、基にする量８回をいくつと見ていますか。

基にする量を１としています。

そうですね。割合は基にする量を１と見たときに、比べる量がいくつに当たるかを意味しています。実は、今日の紙を折る作業の問題でも、全部の紙の枚数が120枚や96枚かもしれないけれど、それを１と見るという発想で考えることもできます｡（以下、時間がある場合は、子供にペアで考えさせる）

※全体を１と見る方法を、子供とのやりとりで確認する。

紙の枚数全体を１とします。
Ａさんが１分で折れる枚数は１÷12で全体の[MATH]\(\frac{1}{12}\)[/MATH]に当たります。
Ｂさんが１分で折れる枚数は１÷８で[MATH]\(\frac{1}{8}\)[/MATH]に当たります。
Ａさん、Ｂさん２人が一緒に作業をすると、１分で折れる紙の枚数は、[MATH]\(\frac{1}{12}\)[/MATH]＋[MATH]\(\frac{1}{8}\)[/MATH]＝[MATH]\(\frac{5}{24}\)[/MATH]に当たります。だから、１÷[MATH]\(\frac{5}{24}\)[/MATH]＝[MATH]\(\frac{24}{5}\)[/MATH]＝4.8で、4.8分になります。

図で確かめたい人もいるかもしれませんね。先生のお勧めは12cmの線を書くことです。12㎝の線だと、12等分すると１㎝ずつに８等分すると1.5㎝ずつになりますね。Ａ、Ｂ２人を合わせると、１＋1.5＝2.5で2.5cmになりますね。12cmの線を2.5㎝ずつ切っていくと、４つ分できて、２㎝あまります。

この残りの２cmが何分になるかを考えます。2.5㎝が1分にあたるから、2cmは0.8に当たります。だから、全部で4.8分ということが確かめられますね。

やっぱり4.8分だ。

紙全体の枚数を１と見ても同じ答えになりましたね。

学習のまとめ

全体の作業の量が分からないときは、全体を公倍数や１と見て考えるとよい。

参考：中学校での文字式を用いた解法
紙の枚数をnとすると、
Ａさん１人だと、ｎ÷12＝[MATH]\(\frac{n}{12}\)[/MATH]分かかる。
Ｂさん１人だと、ｎ÷８＝[MATH]\(\frac{n}{8}\)[/MATH]分かかる。
２人では１分間で[MATH]\(\frac{n}{12}\)[/MATH]＋[MATH]\(\frac{n}{8}\)[/MATH]＝[MATH]\(\frac{5n}{24}\)[/MATH]枚折ることができる。
２人で折ったときにかかる時間は、
ｎ÷[MATH]\(\frac{5n}{24}\)[/MATH]＝ｎ×[MATH]\(\frac{24}{5n}\)[/MATH]＝[MATH]\(\frac{24}{5}\)[/MATH]＝4.8

次の問題は紙を折る場面ではありませんが、同じように考えてみましょう。

評価問題

ある空の水そうに、Ａのじゃ口で水を入れると10分、Ｂのじゃ口で水を入れると15分かかります。ＡとＢの両方で同時に水を入れると、何分でいっぱいになりますか。水そう全体の量を「公倍数のかさ」や１と見て考えましょう。

子供に期待する解答の具体例

・水槽全体の量を、10と15の最小公倍数の30Lにして考えました。　
Ａの蛇口で１分間に入れることができる水の量は、30÷10＝３（L）。
Ｂの蛇口で１分間に入れることができる水の量は、30÷15＝２（L）。
ＡとＢを一緒に使うと、１分間に３＋２＝５（L）入れることができる。
30÷５＝６だから、６分でいっぱいになる。

・水そう全体の量を、１と見て考えました。　
Ａの蛇口で１分間に入れることができる水の量は、１÷10＝[MATH]\(\frac{1}{10}\)[/MATH]で全体の[MATH]\(\frac{1}{10}\)[/MATH]に当たる。
Ｂの蛇口で１分間に入れることができる水の量は、１÷15＝[MATH]\(\frac{1}{15}\)[/MATH]で全体の[MATH]\(\frac{1}{15}\)[/MATH]に当たる。
ＡとＢを一緒に使うと、[MATH]\(\frac{1}{10}\)[/MATH]＋[MATH]\(\frac{1}{15}\)[/MATH]＝[MATH]\(\frac{5}{30}\)[/MATH]＝[MATH]\(\frac{1}{6}\)[/MATH]だから、１分間に全体の[MATH]\(\frac{1}{6}\)[/MATH]入れることができる。
１÷[MATH]\(\frac{1}{6}\)[/MATH]＝６だから、６分でいっぱいになる。