子供の素朴な理解から生じた間違いに付き合う【｢系統」を見通し、学年ごとに押さえる！ つまずきなしの「分数」指導法 #6】

前回は、大きさの等しい分数に関する授業づくりについて、新潟市立上所小学校の志田倫明先生に説明していただきましたが、今回は、そのような授業が求められる理由とともに、もう１つの内容である、分数の加法、減法の授業づくりについて説明していただきます。

子供たちは分数を多様な見方で捉え、間違える場合がある

前回最初に触れた通り、４学年では２、３学年での分数の学習をその延長で広げていく学習をするのですが、子供たちは３年のときの学習経験があるため、分数を多様な見方で捉え、間違える場合があります。例えば、前回紹介したような量として用いられている分数を、２学年で学習した、異なる折り紙を等分するような分割の見方で見ることがあります。これは初回に概説したように、決して子供が間違っているのではなく、分割の見方で見ているわけですから、この子が獲得した学びを生かしている姿には違いありません。ただし、大小比較をする場面には合わないために、４等分したものの３つ分、６等分したものの３つ分というだけでは、この場面での用い方としては説明できていないわけです（資料１参照）。

【資料１】

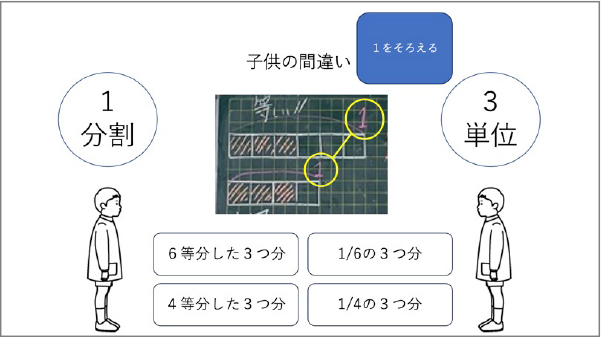
そこで、｢単位分数の幾つ分」という見方をしている子供が説明し、修正にかかります。そうすると、１の大きさが違うので、ちゃんとした単位分数を出すには、もとになる１を揃えなければいけないという話になるのです。このように、用い方の違いによってズレたところが間違いとして表出するので、そこに多様な見方が出てきます。そこで対話を通し、｢比較するのでなければ、この見方でもいいんだよ」｢でも、比較するなら単位分数の幾つ分で比較しなければならない」と学習をしていくと、まず１が揃っていることを確認するようになるのです。

ちなみに先の授業後、私にクレームを言いに来た子供がいました。｢今日、どっちのほうが大きいですか、という問題があったけど、あれって等分するものの大きさによると思うんですよ」と言い、異なる大きさのものを分割をすることは生活の多様にあるという話をした上で、前提となる条件が抜けていると話してくれたのです。その姿を見て、｢ああ、子供たちは自分で責任をもって学んでくれているな」と頼もしく思いました。

習熟が弱い場合には、改めて誤答も取り上げながら、考えて計算する

さて、次に簡単な分数の計算（加法、減法）の学習ですが、抽象的な式表現だったものを量として、図として捉え直し、これを言葉として「単位分数の幾つ分」と表現させました。その過程で、単位が揃っているときに計算できるということを理解していったと思います。

しかし、４学年の簡単な分数の加法、減法の学習で、[MATH]\(\frac{3}{5}\)[/MATH]＋[MATH]\(\frac{4}{5}\)[/MATH]を考えるときに、これまでの学習では基本的に１を超える分数はなかったため、[MATH]\(\frac{3}{5}\)[/MATH]＋[MATH]\(\frac{4}{5}\)[/MATH]＝[MATH]\(\frac{7}{5}\)[/MATH]とすることができず､（分母と分子を両方ともたし合って）[MATH]\(\frac{7}{10}\)[/MATH]としてしまう子供が出てくるのです。それについては、学習指導要領の解説（p194～195）にも、図とともに示されています（資料２参照）。

【資料２　学習指導要領解説より】

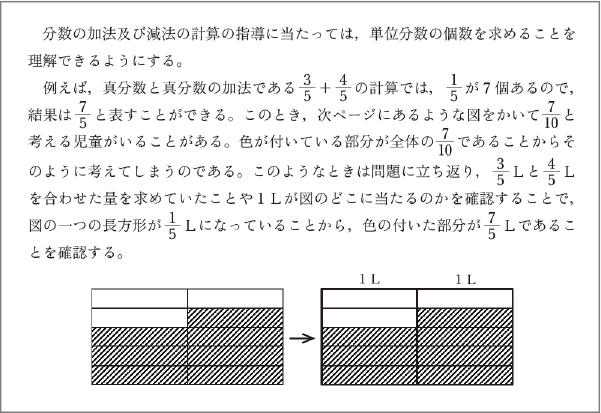
この解説でも、３学年のときにdLマスで学習したような例が示されていますが、このような学習がきちんと習得されていれば、[MATH]\(\frac{1}{5}\)[/MATH]が３つ分と[MATH]\(\frac{1}{5}\)[/MATH]が４つ分をたすと、[MATH]\(\frac{1}{5}\)[/MATH]が７つ分になる。それは単位が揃っているからできる、ということが確認できると思います。しかし習熟が弱かった場合には、改めて誤答も取り上げながら、考えて計算してみてもよいでしょう。ちなみに私の場合は、３学年で扱っていますし、５学年の異分母分数の計算を重めに扱いたいので、ここは軽く扱いたいと考えます。

子供自身が矛盾を修正し、異なる見方を使い分けられるようにする

もう１点、ここで確認しておきたいのは、概説の全国学力調査の例や、２学年の学習の最後に触れた、分割と量の用い方が混在してしまっている問題です。

【資料3】

実際に私も授業で扱ったのですが、２mのテープを示して「[MATH]\(\frac{1}{3}\)[/MATH]mって、どこだろうね？」と問いかけるのです（資料３参照）。すると、大半の子供が指し示すのが２mの[MATH]\(\frac{1}{3}\)[/MATH]、つまり[MATH]\(\frac{2}{3}\)[/MATH]mの位置です。やはり量よりも具体物を分割する分数のイメージが強いのです。この分割の見方に対し、教師がすぐに修正をかけても剥落しやすく、子供自身が修正していかなければ本質的な理解にはつながりにくいので、ここではまず子供たちの意見を良しとします。

その上で、そう考えた理由を聞くのです。そうすると、｢だって[MATH]\(\frac{1}{3}\)[/MATH]mは３つに分けたものの１つ分だもん」と、まさに分割の用い方で説明をします。さらに、「同じ長さだけ３つに分けたので、３等分って言わなきゃダメだよ」などと説明するのです（資料４参照）。ここで、私が「その通り！　上手な説明だね」と言うと、子供たちは「[MATH]\(\frac{2}{3}\)[/MATH]mも分かるよ！」と言います。｢えっ！　[MATH]\(\frac{2}{3}\)[/MATH]mも分かるの？　どうして[MATH]\(\frac{2}{3}\)[/MATH]mも分かるの？」と、さらに子供たちの論理に乗ってあげると、｢[MATH]\(\frac{2}{3}\)[/MATH]mはここだよ」｢[MATH]\(\frac{1}{3}\)[/MATH]mの２つ分だから、ここが[MATH]\(\frac{2}{3}\)[/MATH]mだよ」と言うので、｢理由まで説明できて、すごいじゃない」と価値付けます。

【資料４】

【資料５】

そうすると、さらに「[MATH]\(\frac{3}{3}\)[/MATH]mはここだよ」と２mの位置を差し、さらに「[MATH]\(\frac{3}{3}\)[/MATH]mは１mとも言うよ」と言いますので、｢そうなんだ。１mとも言うんだね。すごいですね」と価値付けてあげます。ここまで説明したところで、｢ちょっとおかしいんじゃない？」と矛盾を指摘する子供が出てきます。そこで、｢今までみんな上手に説明していたけど、『おかしい』ってどういうこと？」と、矛盾を指摘した子に説明を求めると、｢[MATH]\(\frac{3}{3}\)[/MATH]mは１mなんだけど、この図では１mの（はずの）位置が、２mになっているから合わないよ」などと説明するわけです（資料５参照）。ここで子供たちが気付いていきます。

そうすると、子供のほうから「そもそも１mって、２mの半分のところだよね」と意見が出てきて、ピッタリになるように修正していこうということになるので、改めて１mのテープを出してあげるのです（資料６参照）。そこから、｢[MATH]\(\frac{1}{3}\)[/MATH]mはここじゃない」と１mのテープを基に考え始め、ここでやっと基の１が出てくるわけです。そこで、｢何が違っていたんだろうね？」と投げかけると、｢さっきのは２mを３等分したものの１つ分、だけどこれは（普遍単位である）１mを３等分した[MATH]\(\frac{1}{3}\)[/MATH]mの長さだ」と、先の分割の用い方と今度の量の用い方を、使い分けて捉えながら修正をしていきます。

【資料６】

この場面では、｢１mの[MATH]\(\frac{1}{3}\)[/MATH]を[MATH]\(\frac{1}{3}\)[/MATH]mと言うんだよ」と最初から教えたほうが楽ですし、授業はスムーズに進みます。しかし、ここで数学的に大切なのは「分割と見ると～」｢量と見ると～」と多角的に見て、状況に応じて適切に使い分けられることですし、そのような力を付けていくことが大切なのです。ですから、子供の素朴な理解（単一の用い方による理解）から生じた間違いに付き合いながら、子供たち自身が矛盾を修正し、異なる見方を使い分けられるようにしていきます。

ここまできたところで、｢じゃあ、最初にみんなが[MATH]\(\frac{1}{3}\)[/MATH]mだと言った、ここは何mと言えばいいんだろう？」と問いを投げます。そうすると、｢これは[MATH]\(\frac{1}{3}\)[/MATH]mが４つ分だから[MATH]\(\frac{4}{3}\)[/MATH]mだろう」という考えが出てくるわけですが、この授業をしたときのクラスの子供たちは、さらに「[MATH]\(\frac{3}{3}\)[/MATH]m（＝１m）と[MATH]\(\frac{1}{3}\)[/MATH]mだから、[MATH]\(\frac{4}{3}\)[/MATH]mだ」と言い出しました。そこで、私は１mと[MATH]\(\frac{1}{3}\)[/MATH]mだから、｢１[MATH]\(\frac{1}{3}\)[/MATH]mと言うんだよ」と教えました。

さらにおもしろいのは、｢[MATH]\(\frac{1}{3}\)[/MATH]が４つ分と考えれば、[MATH]\(\frac{1}{3}\)[/MATH]×４ですよね」と言う子も出てきます。これは指導内容ではないのですが、子供は今までの式の意味に照らし合わせ、このように式化したわけです。その他に、２mの[MATH]\(\frac{1}{3}\)[/MATH]は[MATH]\(\frac{2}{3}\)[/MATH]mだから、｢[MATH]\(\frac{2}{3}\)[/MATH]＋[MATH]\(\frac{2}{3}\)[/MATH]で[MATH]\(\frac{4}{3}\)[/MATH]mだ」という意見も出てきました。

このような学習は、分数の多様な用い方を捉えることだけに留まらず、簡単な分数の計算にもつながっていくのです。

執筆／教育ジャーナリスト・矢ノ浦勝之

つまずきなしの「分数」指導法
■子供たちが自ら数直線やテープ図をつくり、縦に見比べていくような学習を行う【｢系統」を見通し、学年ごとに押さえる！ つまずきなしの「分数」指導法 #5】
■単位分数を変えながら数直線づくりをし、分数も数であると意識させる【｢系統」を見通し、学年ごとに押さえる！ つまずきなしの「分数」指導法 #4】
■｢もとになるもの」については、しっかり意識付けをしていく【｢系統」を見通し、学年ごとに押さえる！ つまずきなしの「分数」指導法 #3】
■２年では、もとの大きさと部分の大きさを常に意識しながら指導 【｢系統」を見通し、学年ごとに押さえる！ つまずきなしの「分数」指導法 #2】
■分数の５つの用い方を理解しておく 【｢系統」を見通し、学年ごとに押さえる！ つまずきなしの「分数」指導法 #1】