小1算数「たし算」指導アイデア《「10といくつ」という数の見方を用いた計算のしかた》
執筆/新潟県阿賀野市市立安田小学校教諭・加藤光
監修/文部科学省教科調査官・笠井健一、新潟市立新津第一小学校・新津第一幼稚園 校園長・間嶋哲

目次
単元の展開
第1時 「10といくつ」という数の見方に着目し、9+4の計算のしかたを考える。
▼
第2時 被加数が9の場合の計算のしかたを考える。
▼
第3時 「10といくつ」という数の見方に着目し、被加数が8や7の場合や計算のしかたを考える。
▼
第4時 被加数が9から6の場合の加法の計算練習、文章問題
▼
第5時 「10といくつ」という数の見方に着目し、3+9の計算のしかたを考える。
▼
第6時 「10といくつ」という数の見方を用いて、いろいろな計算のしかたを考える。
▼
第7時 計算カードを使って1位数どうしの繰り上がりのある加法の計算の練習
▼
第8時 計算カードの並び方について、関数的な見方を考える。
▼
第9時 1位数どうしの繰り上がりのある加法の問題づくり
▼
第10時 学習内容の習熟・定着
本時のねらい
加数と被加数の2つを分解することによって、10のまとまりをつくれることに気付き、繰り上がりのある加法の計算ができる。
評価規準
- 「10といくつ」という数の見方を用いて、8+6の計算ができる。(知識・技能)
- 加数分解、被加数分解の考え方や、5と5を合わせて10をつくるという考え方など、いろいろな方法を考えている。(思考・判断・表現)
- これまでの学習と関連付けて、いろいろな計算のしかたを考えようとしている。(主体的に学習に取り組む態度)
本時の展開

学校で うさぎを8わ にわとりを6わ かっています。ぜんぶで なんわ 生きものを かっていますか。
“ぜんぶで” と書いてあるからたし算です。
式は8+6です。
たし算の計算はどのように説明できましたか。
説明カードの言葉を使うと、うまく説明ができました。
「10のまとまり」「○と□にわける」「たすかず」「たされるかず」の4つのカードだね。
まいさんはブロックの数をたし算で求めています。どのように計算しているか分かりますか。
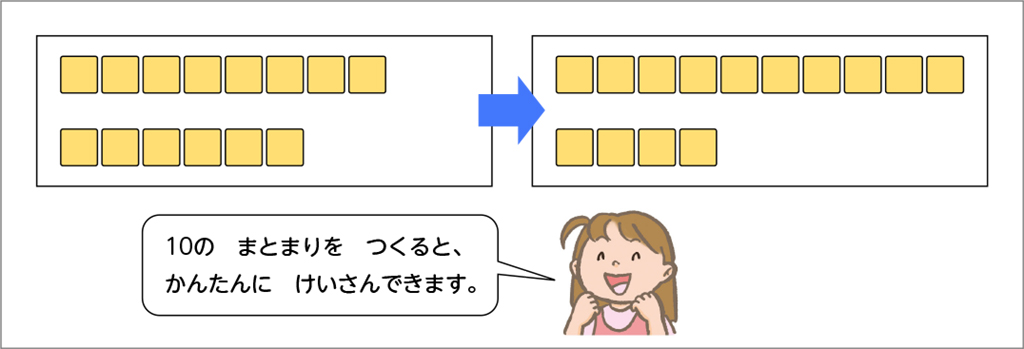
10のまとまりをつくってから答えを求めているね。
ペアになって、まいさんのようにブロックを使って計算のやり方を説明し合いましょう。
※黒板の掲示物を示し、説明のしかたを想起させる。

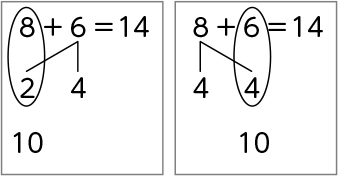
まず、10のまとまりをつくるには、8とあと2です。
足す数の6を、4と2に分けます。
足される数の8と2で10です。
10と4で14です。
※代表児童にブロックを黒板上で動かしながら計算のやり方を説明させる。
足す数の6を分けても説明できますか。
足す数と足される数を交換すると説明できます。
まず、10のまとまりをつくるには、6とあと4です。
足される数の8を4と4に分けます。
足す数の6と4で10です。
10と4で14です。
ブロックを使わないで式でも説明できます。
昨日の勉強のように、足される数の8を分けても計算できます。
2つの計算のやり方があったのですね。はるとさんもブロックの数をたし算で求めています。どのように計算しているか分かりますか。
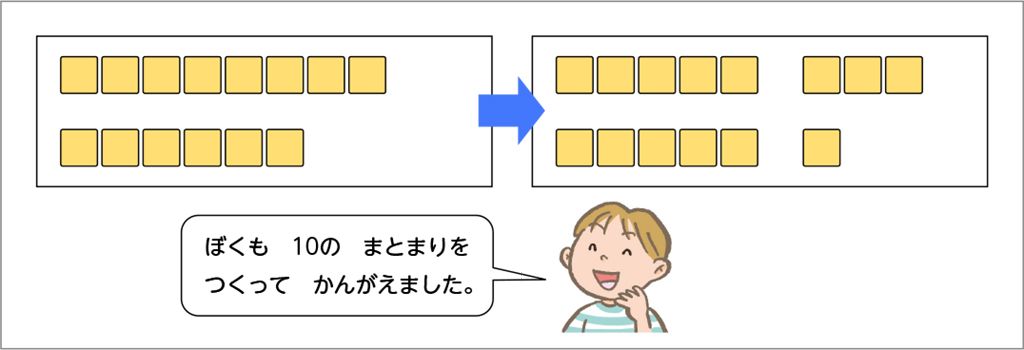
10のまとまりはどこにあるのかな。
8と6の両方を分けているよ。
はるとさんはどのように考えたのかな。

はるとさんはどのように10のまとまりをつくったのかな。
見通し
これまでのやり方との違いは何でしょう。
8と6の両方を分けています。
足される数も足す数も分けているね。
どうして両方とも分けているのかな。
では、今までのやり方とは違うから、説明カードも役に立たないですね。
いえ、説明カードは使えそうな気がします。
同じようにブロックを動かして考えたいな。
式にするとどうなるのかな。
では、ワークシートを配ります。はるとさんのやり方を考えてみましょう。
※説明の方法としてブロックと式の方法があることを確認し、目標「ブロックで説明できる」、チャレンジ目標「式で説明できる」を設定する。
自力解決の様子
A つまずいている子
どのように10のまとまりをつくったかが分からず、説明できない。
B 素朴に解いている子
ブロックを使って、8を5と3、6を5と1に分け、5と5で10のまとまりをつくって説明している。
C ねらい通り解いている子
ブロック操作により、5と5で10のまとまりをつくることに気付き、式に表すこともできる。
学び合いの計画
自力解決後、課題解決の進捗状況(A児、B児、C児がそれぞれ何人いるか)を確認し、グループで考えを伝え合う場を設定します。
その際、一方的に「話し合いましょう」と指示するのではなく、子供に「ほかの人の考えが気になる人はいますか?」というように問いかけ、子供の話し合いたいという思いを確認してから話合いを行うようにします。
また、話合いの目的として、全員が「目標:ブロックで説明できる」に到達できること、より多くの子供が「チャレンジ目標:式で説明できる」になれるように、たくさんの人と話合いをすることを呼びかけます。
全体発表とそれぞれの考えの関連付け
「目標:ブロックで説明できる」を達成した人はいますか。
イラスト/横井智美

