小３算数「何倍でしょう」指導アイデア《基準量の求め方を図や式を用いて説明しよう》

特集: 1人1台端末時代の｢教科指導のヒントとアイデア｣

2024.01.29

単元の展開

第１時　比較量を求める場合には乗法を用いればよいことを、図や式を用いて考え、説明する。
▼
第２時　倍を求める場合は除法を用いればよいことを、図や式を用いて考え、説明することができる。
▼
第３時（本時）基準量を求める場合には、□を用いて乗法の式に表し、除法を用いて□を求めればよいことを、図や式を用いて説明することができる。

本時のねらい

基準量を求める場合には、□を用いて乗法の式に表し、除法を用いて□を求めればよいことを、図や式を用いて説明することができる。

評価規準

基準量の求め方を、数量の関係や図、□を使った用いた式などを用いて考え、説明している。

倍を求める場合は除法を用いればよいことを図や式を用いて考え、説明することができる。

本時の展開

今日は次のような問題を考えてみましょう。

つくえの長さは、クリップの８倍で40㎝です。クリップの長さは何㎝ですか。

前に勉強したときには、倍を求めたり倍を使って長さを求めたりしたけど、今日はちょっと違う感じがする。

何が違うのか、分かりますか。

倍が分かっているのと、大きい長さが分かっています。

この関係を分かりやすくするためにはどうしたらいいですか。

図に表してみます。

では、この関係を図に表してみましょう。

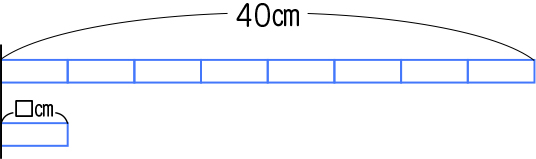
こうやって図に表してみるとできそう。

クリップの８個分ということだよね。

では、どうすればクリップの長さを求めることができるのか考えてみましょう。クリップの大きさを□として、この問題をかけ算の式に表すと、どうなりますか。

クリップの大きさの８倍が40㎝だから、□×８＝40になります。

本時のねらい

クリップの長さを求める方法を考えよう。

自力解決の様子

A　つまずいている子
・解決の見通しをもつことができない（□を求める方法が思い付かない）。

Ｂ　素朴に解いている子
・倍が分かっていることから、かけ算で演算を決定し、そこからかけ算九九を用いて解決している。

Ｃ　ねらい通り解いている子
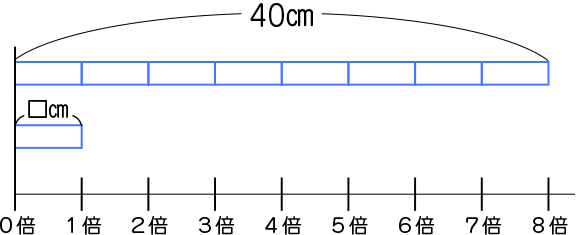
・図のなかに倍のスケールを書き加え、わり算で演算決定し、答えを求めている。

自力解決の様相から、子供たちを評価します。

前時までに、｢比較量を求める」｢倍を求める」という学習をしてきています。

わり算の学習と同様に、子供たちは「５」という数値を求めるために、かけ算で求めることが考えられます。前時の学習のなかでも、こうした解決が見られることが考えられます。

かけ算とわり算との関係をそれぞれの逆算と考えると、かけ算による解決も１つの方法として価値付けていくようにしましょう。

そうしたうえで、｢図に表してみるとどうなるかな？」｢どうして、５㎝が答えなのに、計算では40が答えになっているのだろう？」というように、「求め方としてはよいが、演算としてもっと適した方法があるのではないか？」と問いかけることが大切です。

そうすることで、演算としてのわり算と答えを求めるためのかけ算という関係を改めて整理することができます。

わり算で解決できている子供に対しても、｢図で表すとどうなるかな？」というように、式だけではなく、式と図を関連付けて考える態度を育てていくことが大切です。

学び合いの計画

学び合いのねらいは、式と図を関連付けること、かけ算とわり算との関係を捉えなおし、演算としてはわり算を用いることを明らかにしていくことです。

前時において、倍を求める際にわり算で演算することを学習しています。そのため、子供たちは演算としてのわり算と、答えを求めるためのかけ算という関係への理解を深める時間としましょう。

その際、かけ算で解決することも、求める数である「クリップの長さ」を□と置くことで、式として求めたい部分を表すことができることも押さえておきましょう。

下の図のように、わり算とかけ算の関係について既習であるわり算の学習を想起しながら、「クリップの長さ（基準量）」を求めるときには、演算として、わり算を用いることを明らかにしていけるとよいでしょう。

こうしたことを全体で共有していくために、｢５は式のどこにあるのかな？」｢答えに５がきているのは、どちらの式だと思いますか？」などと子供たちに問いかけ、ときにはペアで話し合い、確認する時間を取ることができるとよいでしょう。

また、自力解決前にはそれぞれの長さのみを示した図から、倍のスケールを書き加え、長さと倍との関係を視覚的に理解しやすい表現をしていくことも大切にしていきましょう。

ノート例

Ａ　つまずいている子

Ｂ　素朴に解いている子

全体発表とそれぞれの考えの関連付け

５×８＝40の式と40÷８＝５の式とを関連付けるようにする。また、それぞれの式と図を関連付けて捉えることができるようにする。

どうやって考えたのか教えてください。

８倍ということはクリップが８個分ということなので、□×８＝40と考えて、□には５が入るので、クリップの長さは５㎝だと分かりました。

どうして５が入ることが分かったのですか。

５×８＝40とかけ算九九で考えました。

僕はわり算を使いました。前の時間にも、答えのところに５が入るほうがよいと勉強したから、わり算で考えました。

図を使って話をすることはできますか。

図を見てみると、40㎝のなかに５㎝が８個分入るということだから、40÷８になります。

このクリップの図を動かしてみると、８個入ることが分かるんですね。倍の線を引いてみましょう。（黒板上で、下の倍のスケールを書き込んでいく）

クリップが１つで１倍、２つだったら２倍……で、８倍が分かっているということは、このクリップ８個分ということが図でも分かります。

この１倍の部分を求めていくということなんですね。

40÷８＝５となるので、このクリップは５㎝になることが分かりました。

前の倍を求めるときと同じで、式はわり算で、答えを求めるためにかけ算を使うんだね。

わり算とかけ算は逆の関係なんだね。

学習のまとめ

全体で共有した図について、全員にこの図をかくように促します。

長さのテープ図と、その下の倍のスケールもともに示すことで、演算の意味がより分かりやすくなることを子供たちに実感させるようにします。

さらに、かけ算とわり算が逆の関係になっているという、倍を求めるときにも子供たちが気付いたことを改めて押さえていくようにします。

説明するときも、式だけではなく具体的に図を操作して示すことや、式と図を関連付けて説明するとより伝わりやすくなることを価値付けていくとよいでしょう。

最後に、評価問題として、同じような場面で数値を変えたものを提示します。ここでは、式と答えだけではなく、図もかくことができるとよいことを伝え、図と式をかくことをめざします。

板書全体を見て、今日の学習をふり返ります。今日はどんなことを学びましたか。

「倍」が分かっているときに、基にする大きさを求めるときはわり算でできます。

わり算とかけ算は逆の関係になっています。

図に表して、図を使って動かしたり、倍の線をかいていったりすると、分かりやすくなります。

では、みんなが話していた、今日学んだことを確認するために、次の問題に取り組みましょう。

評価問題

21㎝の筆箱は小さいクリップの７倍の長さです。小さいクリップは何㎝でしょう。

子供に期待する解答の具体例

□×７＝21
21÷７＝３　　　　　　　
答え　７㎝

まとめとして、｢倍」が分かっているときに「基の大きさ」を求めるときにはわり算を使うことを押さえますが、この評価問題で、図をかくことができているか、問題を解決するための演算としてのわり算と計算の結果を求めるためのかけ算との関係を理解しているかを見とります。

この問題の様相によって、個別の指導をします。

または、次時において、学習をふり返ることから始めるなど、教師がどのような手立てを取るかの指針となります。

感想例

はじめ、どんな式か分からなかったけれど、みんなの話を聞いて基の大きさを求めるには、わり算でやればよいということが分かった。
問題を□を使ってかけ算の式に表してから、□を求めるのは、わり算を使えばよいことが分かった。

学習感想は、ただ分かったことを書くだけではまとめの内容と変わらなくなってしまいます。
分かるようになったきっかけは誰の話なのかを記述したり、知識だけではなく、図を使うよさやかけ算とわり算との関係について書いたりしている子供がいたら、そうした子供のノートを紹介するなどして、ふり返る視点を指導していくとよいでしょう。

イラスト／横井智美

【関連記事】

1人1台端末時代の｢教科指導のヒントとアイデア｣シリーズはこちら！