小５算数「わり算と分数」指導アイデア《分数倍の意味について考える》

特集: 文部科学省教科調査官監修｢教科指導のヒントとアイデア｣

2024.01.17

単元の展開

第１時　分数の意味に着目し、整数の除法の結果を分数で表す方法を考える。
▼
第２時　商分数の適用問題
▼
第３時（本時）整数倍や小数倍の意味を基に、分数倍の意味について考える。
▼
第４時　分数の意味に着目し、分数を小数や整数で表す方法を考える。
▼
第５時　小数や整数の意味に着目し、小数や整数を分数で表す方法を考える。

本時のねらい

整数の除法の結果を分数で表す方法を基に、整数倍･小数倍から分数倍へと、倍の意味を広げて考える。

評価規準

分数の表現に着目し、整数倍･小数倍から分数倍へと、倍の意味を広げて考えている。（思考･判断･表現）

本時の展開

赤、青、黄、白の４本のテープがあります。赤、青、黄のテープの長さは、白のテープの長さのそれぞれ何倍ですか。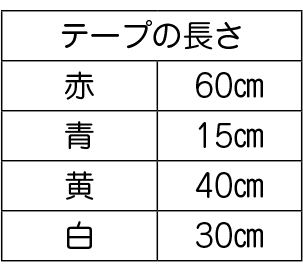

赤、青、黄のテープの長さは、白のテープの長さのそれぞれ何倍になるか分かりますか。

簡単に分かります。今までに習っています。

まず、赤のテープは白のテープの２倍とすぐ分かります。式は60÷30＝２です。

白のテープの長さ30㎝を基にする数にして、わり算をすればいいね。

基にする数で割れば、何倍になるのかを求められるよね。

青のテープは、白のテープより短いから１より小さい数の倍になるね。

青のテープは0.5倍です。式は15÷30＝0.5です。

黄のテープは40㎝だから、40÷30。割り切れるかな。

割り切れないときは、どうやって何倍であるのかを表すのかな。

黄のテープは、1.3333……倍になります。40÷30＝1.3333……だからです。

きちんとした数にならないと落ち着かないな。

40÷30＝[MATH]\(\frac{4}{3}\)[/MATH]だから、[MATH]\(\frac{4}{3}\)[/MATH]倍と言えばどうかな。

倍に分数を使ってもよいのかな。

みんなで、分数でも倍を表すことができるのかを考えていけばよさそうですね。今まで学習したことを生かして、何倍を表す方法について考えていきましょう。

整数や小数だけでなく、分数でも倍を表すことができるのかを考えよう。

見通し

何倍になるのかを、見当を付けて考えよう。（方法の見通し）

整数倍や小数倍の求め方を基にして考えよう。（方法の見通し）

比べる数を基にする数で割ると、何倍になるのか分かるので計算しよう。（方法の見通し）

自力解決の様子

A　つまずいている子
｢15÷30＝0.5だけど、１より小さくなるので、どうすればよいのかな」
（整数倍のように、いくつ分と数えることができないので、どうしてよいか分からない｡）
・倍を求めるために、わり算を使うということは分かっている。
・「いくつ分」のイメージが抜けきらないので、１より小さい数の倍が腑に落ちないでいる。　

Ｂ　素朴に解いている子
｢40÷30＝1.333……。割り切れないので困ったな」　
（小数倍までは表せているが、割り切れないために、その処理に困っている｡）
・何倍かを求めるためには、比べる数を基にする数で割ればよいことを理解している。
・何倍かを整数や小数を用いて表すことができることは理解している。
・基にする数と比べる数との大小関係によって、１より小さい倍があることも理解している。

Ｃ　ねらい通り解いている子
｢40÷30＝[MATH]\(\frac{4}{3}\)[/MATH]。[MATH]\(\frac{4}{3}\)[/MATH]倍とすればよさそう」
（小数倍ではすっきりと表せないので、分数で倍を表すことを考えている｡）
・整数のわり算の結果を分数で表したことを生かして、分数で倍を表そうと考えている。
・整数や小数と同じように、分数にも倍の意味をもたせることができると考えている。
・分数で倍を表すことができるのかを、図で表しながら説明しようとしている。
・整数倍や小数倍の意味を基に、倍について「１と見たときに〇にあたる」というように統合的に捉えている。