小６算数「およその面積と体積」 指導アイデア《およその体積や容積の求め方》
執筆／筑紫野市立吉木小学校教諭・前川恭平
監修／文部科学省教科調査官・笠井健一、福岡教育大学教授・清水紀宏
目次
単元の展開
第１時 身の回りのもののおよその面積について、方眼を工夫して数えて求め方を考える。
▼
第２時 地図上の複雑な図形の概形を捉え、都市などのおよその面積の求め方を考える。
▼
第３時（本時）いろいろな立体の概形を捉え、およその体積や容積の求め方を考える。
▼
第４時 学習内容の定着・習熟を図る。
本時のねらい
立体図形の概形を基本図形として捉え、およその体積を求めることができる。
評価規準
平均を活用し、立体図形のおよその体積を求めることができる。（思考・判断・表現）
本時の展開
これまでに学んだ立体のうち、体積を求められる立体を言いましょう。
直方体です。
立方体です。
角柱です。
円柱です。
そうですね。角柱や円柱は、底面積×高さで求めることができます。それでは、今日はこのプールのおよその体積を求めていきます。（プールのイラスト・写真を提示する）
このプールの形は、どんな立体と言えますか。
直方体です。
でも、深いところと浅いところがあるから、きれいな直方体ではないのではないでしょうか。
そうです。この見取り図を見てください。（見取り図を提示する。）
学校のプールに入る水のおよその体積を求めます。次のプールには、およそ何㎥の水が入るでしょう。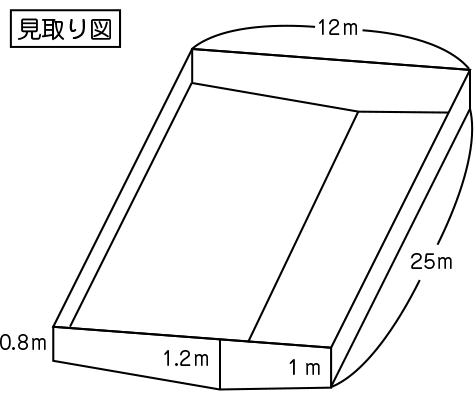
やっぱり直方体ではないね。
およその面積の学習と同じように、プールを直方体と見るとよいと思います。
そうですね。このプールの形を直方体と見ると、およその体積を求めることができそうです。では、このプールの形を直方体と見て、およその体積を求めていきましょう。
プールを直方体と見て、およその体積を求めよう。
※真上からの図と、正面からの図を提示する。
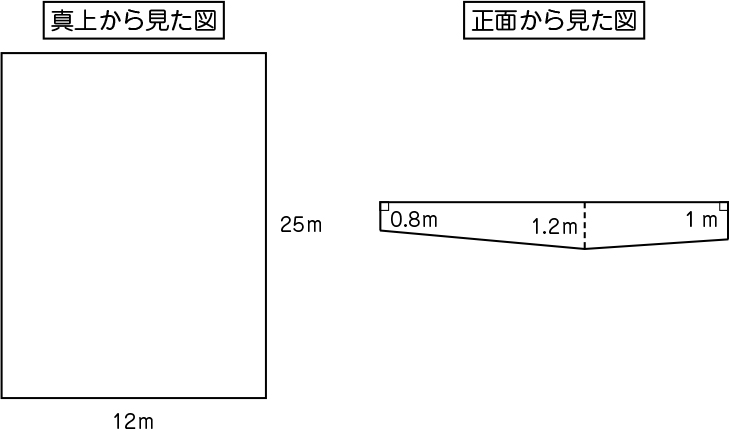
もう一度確認します。直方体の体積の求め方は何ですか。
底面積×高さです。
真上から見た図を底面とすると、底面積は何㎡ですか。
12×25＝300で300㎡です。
このとき、高さは何ｍだと思いますか。
数値が３つあります。高いところと低いところがあって高さを求められません。
高さをどれかにそろえればいいのかな。
ではヒントを出します。プールの形を直方体と見るには、正面から見た形をどのような形と見たらよいですか。
直方体の面は全部長方形だから、正面から見た形を長方形と見たらよいと思います。
長方形が見えたら、高さも決まると思います。
少しずつ見通しをもててきていますね。では、正面から見た図を長方形とみなして、図に鉛筆で長方形をかいてみましょう。
導入では、まず、｢プール」のイラストや写真を提示し、プールがどんな形かを想起させます。
多くの子供が直方体と捉えると思いますが、見取り図を見たときに、プールは水が流れやすくなるように坂がついているため、直方体ではないということに一旦、気付かせます。
この立体のおよその体積を求めていくためには、前時のおよその面積の学習から類推して、プールの体積もこれまでに学んだ図形と見ればよいことに気付かせ、プールを直方体と見て、およその体積を求めるという本時学習のねらいへとつなげていきます。
上の展開では、プールの形を直方体と見ていることから、正面から見た図を長方形と見て、高さを考えていくという見通しをもたせる展開としています。
なお、プールの前の面を底面、高さ25ｍの五角柱と捉える子供もいるかもしれません。この場合は、五角形の面積が正確に計算できないことを確認し、この五角形を長方形と見ていくように方向付けるという展開が考えられます。
子供の実態に応じては、どちらを底面と見るかを子供に選ばせて自力解決をさせるという展開も考えられます。
見通し
・（直方体の体積）＝（底面積）×（高さ）
・正面から見た図を長方形と見て高さを求める。
自力解決の様子
A つまずいている子
・正面の図を長方形と見ることができない。
Ｂ 素朴に解いている子
・正面の図形を長方形と見ることができているが、五角形より小さい形や大きい形で捉えている。
・縦が１ｍの長方形と見ているが、その理由について考えていない。
Ｃ ねらい通り解いている子
・３つの高さを平均して、縦が１ｍの長方形と見ることができている。 ３か所の高さの平均を求めると､（0.8＋1.2＋１）÷３＝１となり、縦が１ｍの長方形となる。
学び合いの計画
学び合いの準備として、子供たち一人一人に正面から見た図を配付し、どのような長方形と見るかかき込ませていきます。このとき、ICT機器を用いて、図に長方形をかき込むことができるようにする環境を準備することも考えられます。
Ａの子供には、正面の図が五角形であることを確認し、その五角形のうち12ｍの辺を使って指で長方形を指し示しながら、面積が同じぐらいの長方形がどのくらいの大きさになるか、フリーハンドでかいてみるよう促します。
Ｂの子供には、前時の学習で学んだことをふり返り、およその面積を求める際に、はみ出た部分と足りない部分が同じくらいになるように考えたことを、ここでも使えないか促します。高さを１ｍと捉えていても、その理由を書いていない子供には、なぜそのように考えたのか、理由を書くよう促しましょう。
学び合いでは、上のようなさまざまな捉え方を確認しながら、よりよい概形の捉え方を考えていきます。
なお、本時は正確な体積を求める問題ではなく、およその体積を求めることが主眼ですから、五角形の面積を正確に求めることができない数値の設定としています。
したがって、Ｂの子供の解法を誤りとするのではなく、実際の面積（ひいては体積）より大きい見積もりや小さい見積もりになっているという扱いが望まれます。
さらに、平均によって決められた高さについても「0.8ｍや1.2ｍより、よい近似になっていること」を押さえることが大切です。
ノート例
Ｂ 素朴に解いている子
全体発表とそれぞれの考えの関連付け
まず、次の２つの考え方を紹介します。
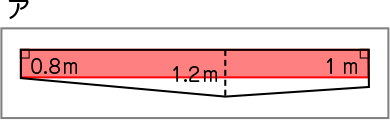
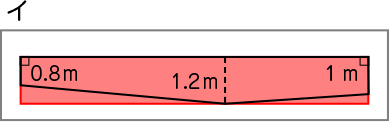
アの考え方では、プールの高さを何ｍと見ていますか。
0.8ｍと見ています。
このときの体積を求めましょう。
底面積が300㎡だから、300×0.8＝240で240㎥です。
※同じようにイの高さと体積を確認する。
この２つの体積とプールの本当の体積との大きさを比べるとどのようなことが言えますか。
アの体積のほうがプールの体積より小さいと思います。
イの体積のほうがプールの体積より大きいと思います。
ということは、プールの本当の体積について確実に言えることがあります。隣どうしで確認してみましょう。
※確認する。
プールの体積は240㎥と360㎥の間だと思います。
そうですね。同じ意味のことを大きい、小さいという言葉を使って言えますか。
プールの体積は240㎥より大きく、360㎥より小さいと言えます。
そうですね。プールの体積がこの範囲にあることが分かってきましたね。
※IＣＴ環境で円の面積の学習で、円の面積を内接する正方形と外接する正方形の間であることを考えた学習をふり返ってもよい。
今、プールの体積のおよその範囲が分かりました。高さについてもおよその範囲は分かりますか。
プールの高さは0.8ｍより長く、1.2ｍより短いと言えます。
そうですね。次のような考えをした人が何人もいました。
縦の長さを何ｍと見ていますか。
１ｍです。
図のどこを見て１ｍと分かりましたか。
右側の深さが１ｍで、それが高さになっています。
この図をかいている人は何人もいましたが、皆さん、右側の深さの１ｍを使ったのですか。
私は３つの高さを平均して、１ｍを求めました。（0.8＋1.2＋１）÷３＝１。このプールの縦の長さの平均は１ｍだということが分かります。
３つの数値を平均しても１ｍが出ましたね。では、これらの高さを１ｍと見る考え方についてどう思いますか。
※ペアまたはグループで話し合わせる。
縦の長さが１ｍの長方形は、はみ出た部分と足りない部分が同じくらいの面積だからよいと思います。（はみ出た部分と足りない部分を指し示しながら説明させる。）
平均を出すと、はみ出た部分と足りない部分がならされるのがよいと思いました。
はみ出た部分と足りない部分を目で見て同じにするのは難しかったです。でも、平均だと計算で高さが出るので簡単です。
どれも素晴らしい気付きですね。今の発表で言ってくれたように、平均は「ならす」という考えなので、この問題を考えるのにとても役立つということですね。それでは、縦の長さを１ｍと見たときのプールに入る水の体積はおよそ何㎥と言えそうですか。（体積を求める時間を確保する。）
12×25×１＝300。プールに入る水の体積は、およそ300ｍ³だと言えます。
そうですね。ところで、この問題では平均の１ｍという結果がプールの右側と同じ数値だったけど、もし、どこかの深さが違っていて、平均と右端の数値が違っているときは、右側の高さと平均の高さのどちらを使ったほうがよいと思いますか。
平均がよいと思います。この問題はたまたま右端と平均が同じだけど、違うときは、ならしている平均のほうが本当の体積に近いと思います。
そうですね。プールの形を直方体と見て、平均も使っておよその体積を求めることができましたね。では、このような花びんの体積はどうでしょうか。
次の四角の花びんの、およその体積を求めましょう。
※この花びんは、上底・下底どちらも正方形。
※ガラスの厚さは考えないものとする。
どのようにして問題を解いていきましょうか。
この形を直方体と見るとよいと思います。
上の面の正方形と下の面の正方形の長さが違うのですが、どうすればいいでしょうか。
辺の長さを平均で求めて、平均の長さの正方形を底面と見ればよいと思います。
それでは、直方体と見ておよその体積を求めていきましょう。
※グループで考えさせる。
花びんを直方体と見て計算しました。上底の１辺の長さ６㎝と、下底の１辺の長さ10㎝の平均の８㎝で考えると、８×８×20＝1280になり、およそ1280㎤です。
この問題でも、平均を使って正方形の一辺の長さを求めて、直方体のおよその体積を求めていますね。
学習のまとめ
およその体積を求めるには、体積を求められる立体と見て計算する。およその長さを求めるとき、平均を使うこともある。
評価課題
下の丸い花びんの、およその体積を求めましょう。
※花びんの上底・下底はどちらも円。
※ガラスの厚さは考えないものとする。
子供に期待する解答の具体例
・この立体を円柱と見る。底面の円の直径を平均で８㎝と捉え、体積を求める。
円柱と見て計算します。
６㎝と10㎝の平均の８㎝を直径と考えると、４×４×3.14×20＝1004.8になります。
およそ1000㎤です。
感想例
- 知っている形と見て、およその体積を求めることができることが分かった。
- およその体積を求める問題で、平均が役に立った。
１人１台端末活用アイデア
子供たちに問題の図を配付し、図の中にかき込めるようにしていくとよいです。また、かき込んだ図を全体で共有して比較できるようにすることで、どの考えがふさわしいか話し合わせるきっかけをつくっていきましょう。
ワークシート（ダウンロード可）
ダウンロードはこちら＞＞
板書例
イラスト／横井智美、やひろきよみ
-
小６体育「体の動きを高める運動【体つくり運動】」指導アイデア
-
小５体育「短距離走・リレー【陸上運動】」指導アイデア
-
小４体育「ゴール型ゲーム【ゲーム】」指導アイデア
-
小３体育「マット運動【器械運動】」指導アイデア
-
小２体育「体ほぐしの運動遊び【体つくりの運動遊び】」指導アイデア
-
小１体育「固定施設を使った運動遊び【器械・器具を使っての運動遊び】」指導アイデア
-
小４国語科「ヤドカリとイソギンチャク」全時間の板書＆指導アイデア
-
小１算数「たすのかな、ひくのかな」指導アイデア《たし算やひき算の演算》
-
小２算数「かけ算⑶」指導アイデア《９の段の九九の構成を通して、答えの増え方や交換法則に気付く》
-
小２算数「かけ算⑵」指導アイデア《物の数の求め方をかけ算を用いて解決する》
