小6算数「比例と反比例」 指導アイデア《比例の式やグラフを用いて、問題解決の方法を考える》

執筆/北九州市立高須小学校教諭・重藤拓也
監修/文部科学省教科調査官・笠井健一、福岡教育大学教授・清水紀宏

目次
単元の展開
第1時 伴って変わる2つの数量の変わり方について考える。
▼
第2時 紙の枚数と紙の重さとの関係を調べ、説明する。
▼
第3時 針金の長さと重さの2つの数量が伴って変わることを調べ、比例の意味について考える。
▼
第4時 比例の性質について考え、比例の関係は式で表すことができることを知る。
▼
第5時 比例の性質を利用して、比例の関係を式で表す。
▼
第6時 xとyの関係を式に表し、決まった数は何を表しているか考える。
▼
第7時 比例の関係をグラフに表すことを考え、かき方と特徴を知る。
▼
第8時 グラフを見て、比例しているかどうかを判断したり、数値を読んだりする。
▼
第9時・10時(本時)比例の関係を表す式やグラフを用いて、問題解決の方法を考える。
▼
第11時 反比例する2つの量の変わり方を調べ、反比例の特徴を考える。
▼
第12時 反比例の性質を見付け、反比例を表す式やグラフについて考える。
▼
第13時 反比例の性質を利用して、問題解決の方法を考える。
▼
第14時・15時 適用問題を解く。
本時のねらい
伴って変わる数量の関係に着目し、道のりや二酸化炭素の排出量の差を考える活動を通して、比例の式を活用して問題を解決できるようにする。
評価規準
複数の比例のグラフから式を求め、その式を活用して、ある道のりにおける二酸化炭素の排出量の差を求めることができる。(思考・判断・表現)
本時の展開

自動車やバスを走らせると、はい気ガスとして二酸化炭素がはい出されます。そこで、さくらさんはそれぞれが走った道のりとはい出される二酸化炭素の量について調べてみました。「1人当たりのはい出量」を調べてグラフにしたところ、おおよそ次のようになりました。グラフからいろいろなことを読み取りましょう。
(問題場面を提示する)このグラフを見てください。
道のりと二酸化炭素の量についての問題だね。
SDGsの学習で、乗り物の排気ガスに二酸化炭素が含まれることを学習したよね。
グラフからどんなことが分かるのかな。
バスのほうが大きいから、バスのほうが二酸化炭素を多く出しそうだよね。
それではグラフを見てみましょう。(PowerPointを用いて、グラフの直線が伸びていく様子を見せる。)
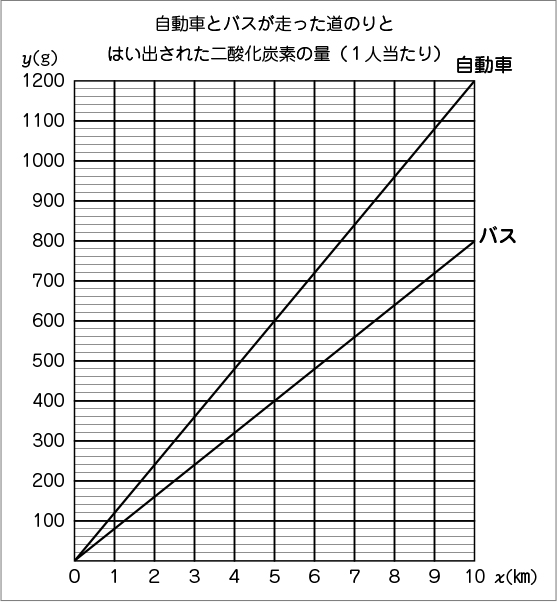
え、自動車のほうが多く出しているよ。
バスのほうが多いと思ったよね。
バスのほうが大きいから、排出される二酸化炭素も多くないとおかしくないかな。
今回の問題は「1人当たり」になっていますね。1人当たりということは、人数が多ければ多いほど、排出される二酸化炭素の量は、どうなりますか。
人数が多くなるほど、1人当たりに排出される二酸化炭素の量は少なくなります。
そうか。バスのほうが一度に乗れる人数が多いから、1人当たりの二酸化炭素の量は少なくなるのか。
だから、1人当たりにすると一度に乗れる人数が少ない自動車のほうが多くなるのね。
このグラフは2本とも(0、0)を通る直線だから、どちらも走った道のりと二酸化炭素の量が比例しているね。
比例のグラフということは、「y=(決まった数)×x」で表せるよ。
今日は、この比例のグラフから分かることについて、いろいろ読み取ってみましょう。

2本のグラフから分かることを考えよう。

自動車とバスが5㎞走るとき、はい出される二酸化炭素の量の差は、何gですか。
自動車とバスがはい出した二酸化炭素が480gになったとき、それぞれが走った道のりの差は何㎞ですか。
※問題①・②を提示する。
問題①は、どのように考えるとよいですか。
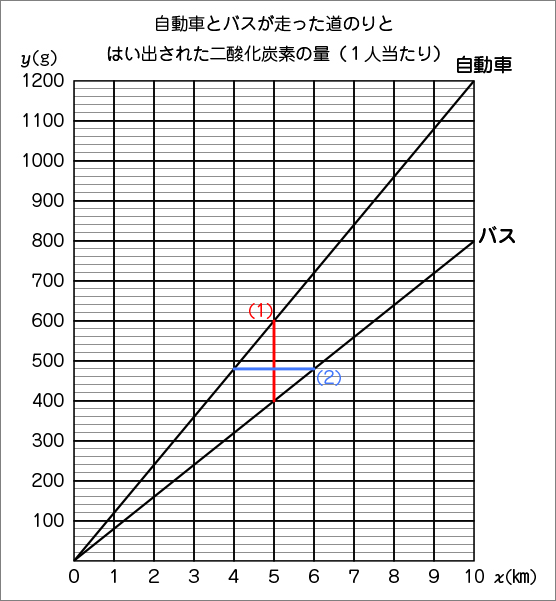
問題①は、それぞれが5㎞進んだときを考えたらいいので、グラフを縦に見て、自動車とバスのグラフがx=5のときのyの値の目盛りの差を読むと分かります。
x=5のときのyの値の目盛りの差は200なので、答えは200gです。(グラフに縦線①を描いて確認をする)
では、問題②はどうですか。自動車とバスが排出した二酸化炭素が480gになったとき、それぞれが走った道のりの差は何㎞ですか。
問題②は、今度はグラフを横に見て、y=480のときのyの値の目盛りの差を読むと分かります。
y=480になるのは、自動車が4㎞、バスが6㎞のときなので、6-4=2で2㎞です。(グラフに横線②を描いて確認をする)
では、問題③について考えていきましょう。

自動車とバス、それぞれの方法でA町からB町までの70㎞移動した場合、はい出される二酸化炭素の量の差は何gですか。
※問題③を提示する。
70㎞のときかぁ。今のグラフからだと分からないね。
いや、ここから先を伸ばせば分かるよ。
確かにグラフの先を書いても分かるけど、そんなに先まで書くよりも楽な方法があるんじゃないかな。
それに70㎞を求めようと思ったら、今の7倍もグラフを伸ばさないといけないから、今は無理だよ。
70㎞のときが知りたいのだから、5㎞のときや10㎞のときの値が使えそうだと思うよ。
式に表したら考えられそう。
見通し
・グラフから値を読み取る。
・「y=(決まった数)×x」を使って計算する。
第6学年では、比例の性質、2量の関係の式表現、比例のグラフについて学習してきています。本時の教材は、他教科(理科や総合的な学習の時間)の学習内容と関連していることもあり、子供にとって関心のあるものです。
導入で、問題場面とグラフを提示する際は、PowerPointを用いて、グラフの直線が徐々に伸びていく様子を見せることで、グラフの特徴から比例の関係であることを捉えられるようにします。
また、2量に着目させることで本時学習のめあてをつかむことができるようにします。
問題①・問題②については、グラフから値を正しく読み取ることが目的なので、クラス全体で確認していきます。それを受けて、③を解決していくようにします。
自力解決の様子
A つまずいている子
自動車やバスの式を求めることができず、70㎞移動した場合の二酸化炭素の量を求めることができない。
B 素朴に解いている子
10㎞のときのyの値から考える方法
バス 10㎞で 800g
↓
70㎞で 5600g
自動車 10㎞で 1200g
↓
70㎞で 8400g
8400-5600=2800 2800g
C ねらい通り解いている子
比例の式を使って考える方法
バス y=80×x
x=70のとき 80×70=5600
自動車 y=120×x
x=70のとき 120×70=8400
8400―5600=2800 2800g
Aの子供に対しては、xとyの関係を式に表すためには、どのようなことを考えることが必要だったかを問いかけ、xとyの関係を式に表すことができるように支援します。
その後、70がxとyのどちらの変数か確かめることで、x=70として計算することができるようにします。
Bの子供に対しては、グラフから読み取った値を基に考えていることを称賛するとともに、どんな場合でも用いることができる方法かを問いかけます。例えば、道のりが37㎞や61㎞を例に出して、いつでも使える方法を考えさせていきます。
学び合いの計画
学び合いの場面では、まずBの考え方を提示し、グラフの数値から10㎞のときの差を読み、7倍していることを理解させます。
その際に、10㎞のときのyの値の差を7倍することで、70㎞のときの差が求められるのは、道のりと二酸化炭素の量排出量が比例関係になっているからであることを確認します。
次にCの考え方を提示し、グラフからバス・自動車がx=1のときのyの値を基に比例の関係式を求めて考えたことを確かめます。
その際に、どちらか一方の式の求め方を全体で確かめた後、もう一方の式の求め方をペアで伝え合う活動を設定することで、比例の関係式の求め方を一人一人が確認できるようにします。
そして、それぞれの式を用いてx=70に対応するyの値を求め、それらの差を求めることで答えを導き出したことを確認していきます。
ノート例
B 素朴に解いている子

C ねらい通りに解いている子

全体発表とそれぞれの考えの関連付け
Bさんの考え方を見ていきましょう。
まずバスを考えます。10㎞のときのyの値を読み取ると、800gになっています。70㎞のときが知りたいから、10㎞のときのyの値を7倍したら、バスは5600gの二酸化炭素を排出することが分かります。
どうして7倍すると分かるのですか。
イラスト/横井智美

