小５算数「図形の角」指導アイデア《四角形の内角の和》

特集: 1人1台端末時代の｢教科指導のヒントとアイデア｣

2023.12.04

単元の展開

第１時　図形を重ね合わせる操作を通して、合同の意味を理解する。
▼
第２時　合同な２つの図形の対応する辺の長さや角の大きさが等しいことを理解する。
▼
第３時　長方形や平行四辺形、台形を対角線で分けてできた三角形を合同の観点で考察する。
▼
第４時　図形の構成要素に着目し､合同な三角形のかき方を考え、作図する。
▼
第５時　合同な三角形を３つの方法で作図する。（技能の習熟）
▼
第６時　合同な三角形の作図のしかたを基に、合同な四角形のかき方を考え、作図する。
▼
第７時　合同な三角形の敷き詰めを通して、内角の和が180°であることを理解する。
▼
第８時（本時）三角形の内角の和が180°であることを基に､四角形の内角の和を調べる。
▼
第９時　三角形や四角形の内角の和を基にして、多角形の内角の和を調べ

本時のねらい

三角形の内角の和が180°であることを基にして、四角形の内角の和が360°であることを筋道を立てて考える。

評価規準

三角形の内角の和が180°であることに着目し、四角形の内角の和が360°であることを筋道を立てて考え、説明している。（思考・判断・表現）

本時の展開

四角形の４つの角の大きさの和を求めましょう。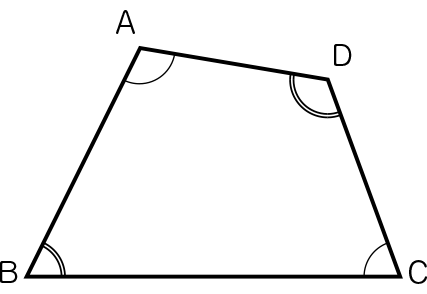

前回は、三角形の３つの角の大きさの和について、いろいろな方法で確かめたり、いろいろな三角形でも和が同じかどうかを調べたりしました。今日は、四角形の４つの角の大きさの和を求めましょう。どうすると求められるでしょうか。

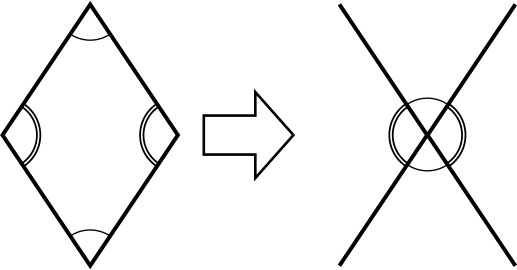
三角形のときは、紙にかいた三角形のそれぞれの角を切り取って、頂点を１つの点に集めると求められました。なので、同じように紙にかいた四角形の角を敷き詰めてみるといいと思います。

そうでしたね。それでは、紙にかいた四角形を切り取って、敷き詰めてみましょう。四角形の４つの角はどうなりましたか。

ぴったりと敷き詰めることができました。

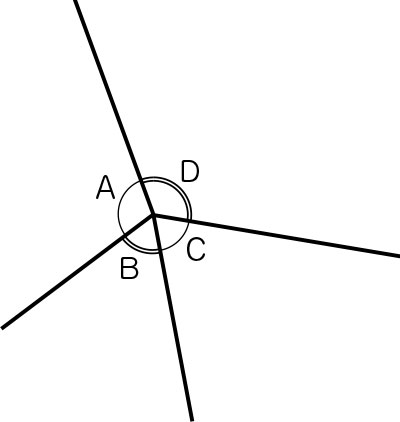
ぴったりと敷き詰められたことから、四角形の４つの角の大きさの和は何度と言えますか。

360°と言うことができます。

四年生のときに、角の大きさは回転の大きさだと学習しました。ちょうど１回転分なので360°です。

では、四角形の４つの角の大きさは360°と言えますか。

いえ、この四角形は360°になりましたが、ほかの四角形ではどうかわかりません。

どんな四角形でも４つの角の大きさは360°になるのかな。

私は、長方形と正方形で確かめてみました。90°が４つだから、360°になりました。

僕は、ひし形を調べてみたよ。４つの角を敷き詰めると、やっぱり360°になったよ。

平行四辺形を試してみたけど、360°でした。

私は、台形を試したけど、みんなと同じで360°でした。

どの四角形も４つの角の大きさの和は、360°になっているね。形が違うのにどうしてどれも360°になるのだろう。不思議だなぁ。

どれも360°になることをどうやって説明したらいいのかな。

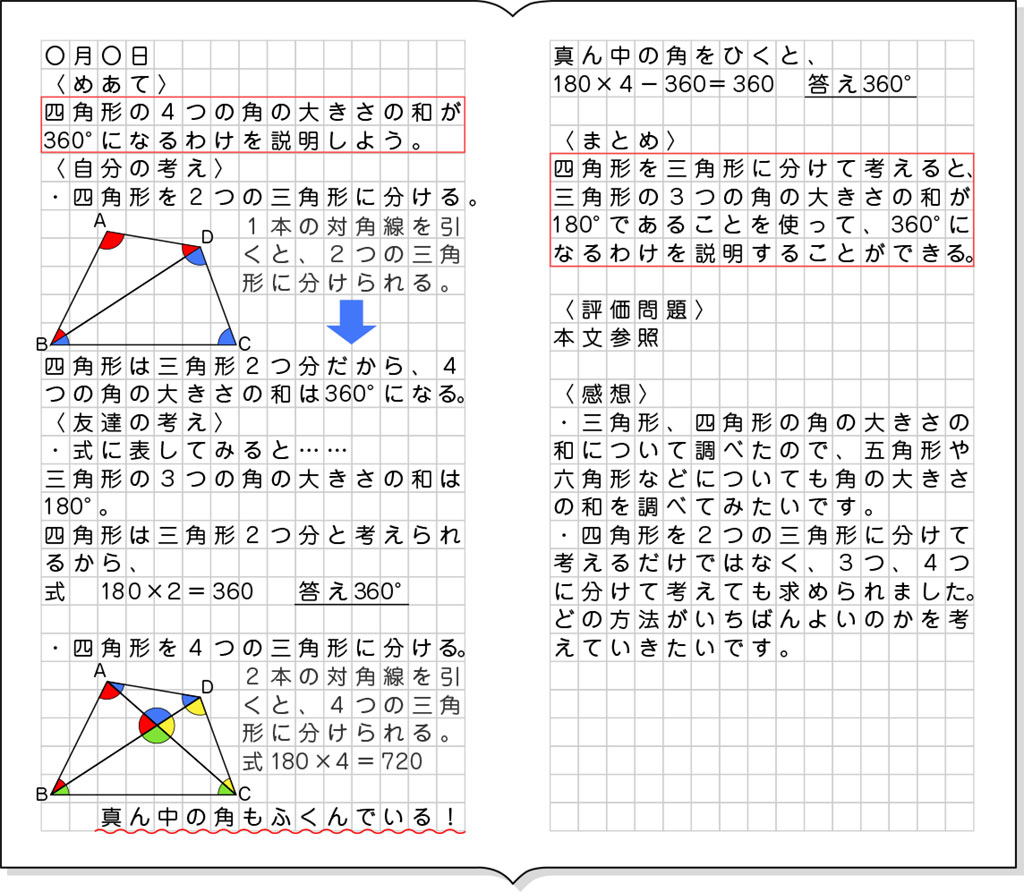
四角形の４つの角の大きさの和が360°になるわけを説明しよう。　

見通し

いろいろな四角形の４つの角を敷き詰めると、どれも360°になった。（見通しの根拠）

どんな四角形でも４つの角の大きさの和は360°になりそうだ。（見通しの予想）

三角形２つ分と見て考えると、四角形の４つの角の大きさの和は180×２＝360で求められることから、四角形の４つの角の大きさの和は、三角形の３つの角の大きさの和の２つ分であると言える。（結果の見通し）

自力解決の様子

A　つまずいている子

正方形や長方形であれば、90°×４＝360°だからと考えている。
・４つの角が90°の特殊な場合についてのみ考えている。

Ｂ　素朴に解いている子

四角形は三角形２つ分だから360°と考えている。
・考えの基になるアイデアを漠然ともってはいるが、筋道立てた説明には至っていない。

Ｃ　ねらい通り解いている子

三角形の３つの角の大きさの和が180°であることを基にして、四角形の４つの角の大きさの和が360°であることを180°×２＝360°の式を用いるなどして、筋道立てて説明している。
・どんな四角形を、どのような求め方をしても、４つの角の大きさの和が360°になることに気付いている。
・四角形の４つの角の大きさの和の求め方は、どれも三角形の３つの角の和180°の２倍に帰着することに気付いている。

学び合いの計画

本時は、前時に学習した三角形の内角の和が180°であることを基に、四角形の内角の和が360°であることを考えていく場面です。その際に、演繹的に考えを進めていくことを経験します。

｢演繹的に考える」とは、｢既に正しいことが明らかになっている事柄を基にして別の新しい事柄を説明していくこと｣（小学校学習指導要領解説算数編平成29年７月　文部科学省）です。

ですから、本時に至るまでに、三角形の内角の和をいろいろな方法で試し、180°であることを確認しておく必要があります。

この活動が充実し、子供たちが実感を伴って理解することにより、本時の活動がより活発なものになると言えます。

本時では、始めに提示した四角形の内角の和が360°であることを具体的に調べます。そこで、｢どんな四角形でも360°になるのか」と投げかけ、これまで学習した四角形をはじめとして、どんな四角形でも内角の和が360°になるのかを確かめる活動を行います。

角を切り取って確かめたり、角を色分けして計算で求めたりする子供たちの姿が予想されるため、必要な図形がかかれた用紙を用意しておくと活動は効率よく進められます。

その後、どの四角形でも内角の和が360°になりそうだということを確かめ、学習のねらいについて考えていきます。

ここでは、四角形の対角線を引き、三角形が２つできることに着目し、前時で確認した三角形の内角の和が180°になることを基に、180°を２倍する考えに焦点を当てていきます。

話合いの場面では、子供たちの発言に対して、｢それは、どういうこと？」｢それは図のどこに表れているの？」など、ていねいに問い返すことで、子供たちは学習のねらいについて深く考えていくことができます。

ノート例

Ａ　つまずいている子

Ｂ　素朴に解いている子

全体発表とそれぞれの考えの関連付け

四角形の４つの角の大きさの和が360°になるわけを説明しましょう。

僕は、正方形や長方形を基にして考えました。正方形や長方形は、４つの角はどれも90°になるから、90×４＝360という計算で求めることができるから、360°になると思いました。

正方形や長方形は、確かにすべての角の大きさが90°だから360°になるというのはわかりやすいね。

でも、角の大きさがはっきりとわからない四角形の場合でも360°になるのはどうしてなのかな。

私は、四角形は三角形２つ分だから、360°になると思います。

それは、どういうことですか。

僕、わかります。四角形に対角線を１本引くと、三角形が２つできるからです。

三角形が２つできると、どうして360°になるの。

だって、前の授業で、三角形の３つの角の大きさの和は180°になると習ったでしょ。つまり、この図の三角形ＡＢＤの角の大きさの和は180°、三角形ＤＢＣの角の大きさの和も180°になるから、この２つを合わせると、360°になると思います。

今の発言は、図のどの部分に表れていますか。

三角形ＡＢＤの角を赤、三角形ＤＢＣの角を青に塗ると、このようになります。すると、四角形の４つの角の大きさの和は、三角形の３つの角の大きさの和の２つ分になっていることがわかります。だから、360°になると思います。

僕はこのことを式に表してみました。三角形が２つ分だから、180×２＝360。だから、四角形の４つの角の大きさの和は360°になります。

色分けをすると、三角形が２つあることがはっきりとわかりますね。表された式も図の通りですね。

私はみんなと同じ対角線を引いたけれど、１本ではなく２本引きました。

どういうことですか。

この図のように引きました。

なるほど。これもなかに三角形ができるから、式がつくれそうだね。

三角形が４つあるから、180×４＝720。あれ？　360°にならないよ。

４つに分けると360°にならなくなるなんておかしい。何か原因があるはずだよ。色を塗ってみようよ。

こうなったよ。

そうか！　真ん中にある角も計算のなかに入っていたから、360°にならなかったんだ。

じゃあ、真ん中の角を引けばいいわけだから、式は180×４－360＝360。ちゃんと、360°になったね。

四角形のなかに三角形をつくれば、180°を基にして考えることができるんだね。

それなら、こういう考え方もできそうだよ。今度は、辺ＢＣの真ん中にある角を引けばよさそうだね。

式に表すと、180×３－180＝360だね。やっぱり360°になるね。

四角形のなかに三角形をつくり、三角形の３つの角の大きさの和が180°であることを基にして、四角形の４つの角の大きさの和を求めることができますね。

学習のまとめ

どんな四角形でも、４つの角の大きさの和は360°になるわけ
⑴　どんな三角形でも、３つの角の大きさの和は180°になる。
⑵　どんな四角形でも、２つの三角形に分けることができる。
⑶　⑴と⑵から、どんな四角形でも、４つの角の大きさの和は、180°の２倍になると言える。180×２＝360

だから、どんな四角形でも内角の大きさの和は360°になると言える。

四角形を三角形に分けて考えると、三角形の３つの角の大きさの和が180°であることを使って、360°になるわけを説明することができる。

評価問題

角Ａの大きさの求め方を説明しましょう。

子供に期待する解答の具体例

四角形の４つの角の大きさの和は360°だから、360°から、角Ｂ、角Ｃ、角Ｄを引くと、角Ａの大きさを求めることができる。それぞれの角の大きさは、60°、90°、90°なので、それらを360°から引くと、角Ａの大きさは120°になる。

式　　360－60－90－90＝120
　　　360－(60＋90＋90)＝120
答え　120°

本時の評価規準を達成した子供の具体の姿

四角形を三角形に分けて考え、三角形の３つの角の大きさが180°であることを使って360°になるわけを説明したことを基に、筋道を立てて角Ａを求める方法を説明している。　

感想例

どんな四角形でも、四角形の４つの角の大きさの和は360°になることがわかりました。
四角形を三角形２つ分と見ると、三角形の３つの角の大きさの和が180°であることを使って、180×２という式で説明できることがわかりました。
筋道を立てた説明がうまくできるためには、何を基に何をはっきりさせるのかを考えて、説明の順をはっきりさせることが大事だと考えました。
２つの三角形に分けて考えるだけではなく、３つや４つに分けて考えても求められました。どの方法がいちばんよいのかを考えていきたいです。
三角形、四角形の角の大きさの和について調べたので、五角形や六角形などについても角の大きさの和を調べてみたいです。
四角形の内角の和をいろいろな方法で求めて式に表したら、どの式も「180×２」に整理することができました。式から、四角形の内角の和を求める見方や考え方もありそうだと思いました。

ワークシート（ダウンロード可）

ダウンロードはこちら＞＞