小6算数「分数のわり算」指導アイデア（2）
執筆／埼玉県公立小学校教諭・松井浩司
編集委員／国立教育政策研究所教育課程調査官・笠井健一、埼玉県公立小学校校長・書上敦志
目次
本時のねらいと評価規準
（本時の位置 ４／ 11）
ねらい
除数と商の関係について考える。
評価規準
1を基準とした除数の大小に着目して、被除数と商の大小関係について、数直線を用いて考え、説明している。（数学的な考え方）
問題
１と[MATH]\(\frac{1}{3}\)[/MATH]m の重さが12g の細いはり金と、[MATH]\(\frac{2}{3}\)[/MATH]m の重さが12g の太いはり金があります。１m の重さは、それぞれ何g ですか。
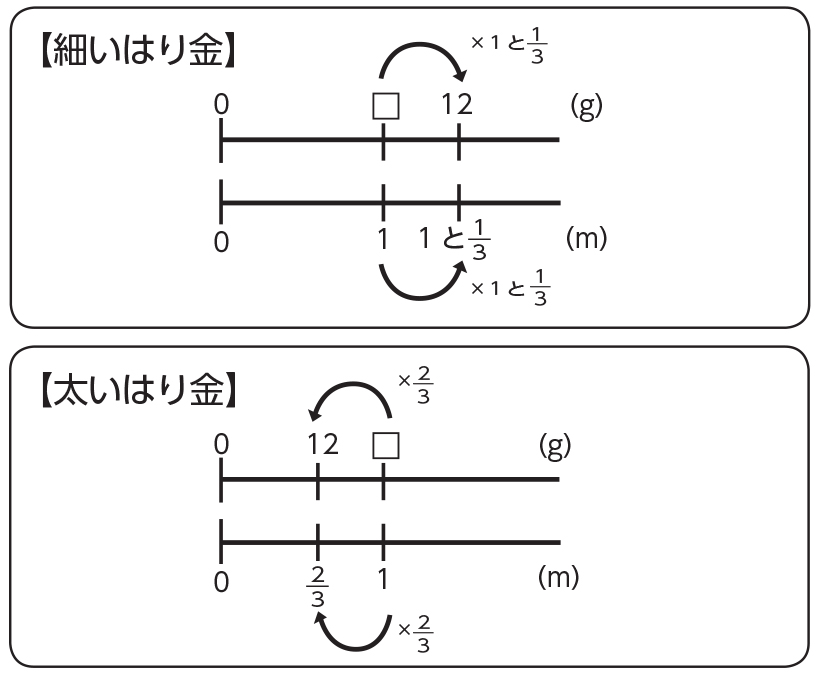
それぞれ数直線に表し、問題を解決しましょう。
～それぞれの問題を解決する～
２つの数直線や式を見比べて、気が付くことはありますか。
どちらも、わられる数が12で同じになっている。
でも、わる数と商は違う。
わる数が変われば、商も変わる。
わる数の大きさと商の大きさは、どんな関係でしょうか。
本時の学習のねらい
わる数の大きさと商の大きさの関係を調べよう。
見通し
まず、これまでの分数の除法の学習を生かして、数直線を用いて解決していきます。そして、問題解決を振り返り、２つの式や数直線を比較することで、本時の学習課題を明確にしていきます。比較する際には、変わるものと変わらないものという視点から、わられる数は変わらず、わる数と商が変わることを引き出します。
自力解決の様子
A つまずいている子
関係を捉えることができない。課題の意味が分からない。
B 素朴に解いている子
わる数が大きくなると、商が小さくなることを説明している。
C ねらい通りに解いている子
数直線と関連させながら、１を基準として関係を説明している。
学び合いのポイント
イラスト／横井智美
『小六教育技術』2018年6月号より
