小4算数「わり算」指導アイデア《72枚のカードを3人で均等に分ける方法を考えよう》
執筆/埼玉県公立小学校教諭・松井浩司
編集委員/文部科学省教科調査官・笠井健一、浦和大学教授・矢部一夫
目次
本時のねらいと評価規準
〔本時3 / 13時〕
ねらい
2位数÷ 1位数(余りなし)の計算のしかたを考える。
評価規準
2位数÷1位数(余りなし)の計算のしかたを既習の除法計算を基に、図や式を用いて考え、説明することができる。(数学的な考え方)

問題
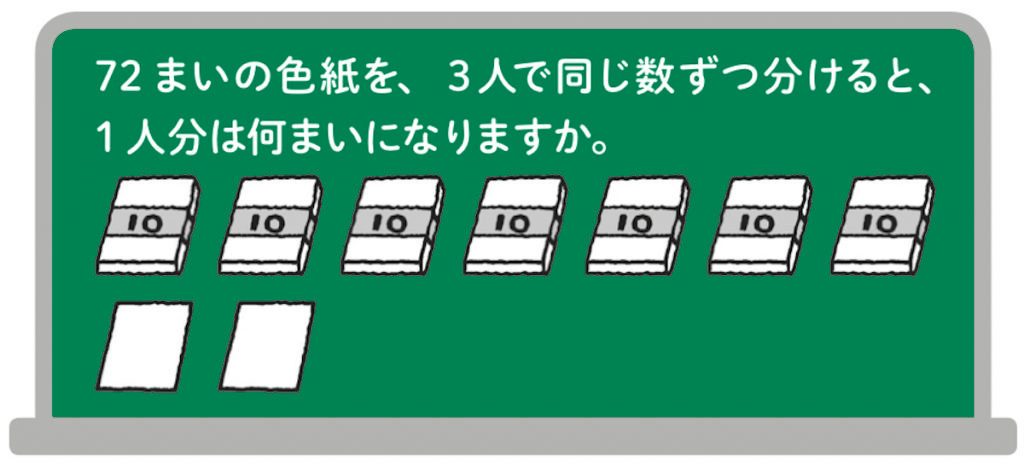
どんな式になりますか。
3人で同じ枚数ずつ分けたときの1人分の枚数を求めるから72÷3です 。
今まで学習したわり算と違うところはどこですか。
3の段を使っても簡単に求められないなあ。
何十÷何はできたけれど、何十だけじゃなくて、ばらがあるよ。
前の時間では10のたばが割り切れたけれど、これではうまく分けられません。(Aさん)
Aさんが言いたいこと、わかりますか。
あ 、わかった 。10のたばで考えると7÷3だけれど、余りが出てしまいます。
10のたばが割り切れないときは、どうするのかな
学習のねらい
10のたばがうまく割り切れない「72 ÷ 3」の計算のしかたを考えよう
見通し
どんな方法で考えますか?
1人分が10 枚、20 枚…と見当をつけながら考えます。
図を使って考えます。
図を式と結び付けながら考えます。
自己解決

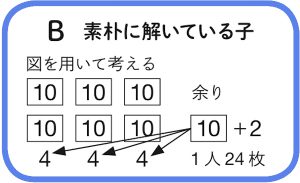

学び合いのポイント
本時は、図的な表現や実際の操作の活動を式とつなげることで、形式的に計算を処理させるのではなく、実感を伴わせながらわり算の意味や計算のしかたを理解させていくことが大切です。
イラスト/小沢ヨマ 横井智美
『教育技術 小三小四』2019年5月号より

