小5算数「小数のわり算」指導アイデア《あまりがある場合の小数で割る除法の計算》

執筆/富山県高岡市立五位小学校教諭・吉田陽
監修/文部科学省教科調査官・笠井健一
前・富山県南砺市立福光東部小学校校長・中川愼一

目次
単元の展開
第1時 問題場面の数量の関係を数直線に表し、除数が小数の除法の意味を捉える。
▼
第2時 除法に関して成り立つ性質を使って、整数÷小数の計算の仕方を考える(除数が1より大きい場合)。
▼
第3時 除数に関して成り立つ性質を使って、整数÷純小数の計算の仕方を考える(除数が1より小さい場合)。
▼
第4時 除法に関して成り立つ性質を使って整数の除法にし、小数÷小数の計算の仕方を考える。
▼
第5・6時 除法に関して成り立つ性質を使って整数の除法にし、小数で割る筆算の仕方を考える。
▼
第7時 被除数を変えずに除数の数を変えたときの商を比較し、除数と商の大きさの関係を理解する。
▼
第8時(本時)除数に関して成り立つ性質を使って筆算し、あまりがある場合の小数で割る除法の計算の仕方を考える。
▼
第9時 除法に関して成り立つ性質を使って筆算し、商を概数で表す方法を知る。
▼
第10・11時 問題場面の基準量と比較量の関係を数直線に表し、倍を表す小数や比較量の求め方を考える。
▼
第12時 問題場面の基準量と比較量の関係を数直線に表し、基準量の求め方を考える。
本時のねらい
割る数が小数であまりがある場合のわり算について、計算の仕方とあまりの大きさについて考える。
評価規準
割る数が小数のわり算について、わり算の意味を捉え直し、あまりがある場合の計算の仕方とあまりの大きさについて考えている。(思考・判断・表現)
本時の展開
問題の□にいろいろな数を入れて、考えてみましょう。

□mのロープを1.2mずつに切って、短いロープをつくります。短いロープを何本つくることができますか。
まずは、□が12のとき、何本つくれるか求めましょう。式や答えはどうなりますか。
12÷1.2になります。
答えは、10本です。
そうですね。では、□が7.2のときはどうでしょう。
式は、7.2÷1.2になります。答えは6本です。
正解です。小数の計算の仕方が身に付いていますね。それでは、□が5.1のときはどうでしょう。

5.1mのロープを1.2mずつに切って、短いロープをつくります。短いロープを何本つくることができますか。
式は、5.1÷1.2になるね。
答えは……、あれ? 商は4になるけど、あまりが出てしまったよ。
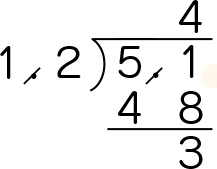
じゃあ、「4本つくれて、3mあまる」が答えだね。
えっ!? 本当に3mでいいのかな。
答えに疑問をもっている人がいるようですね。では、この問題は、□が12や7.2のときとどう違うのか、整理してみましょう。
この問題は、あまりが出る問題になっています。
そうですね。それでは今日、みんなで考える問題にするために一文書き加えます。

5.1mのロープを1.2mずつに切って、短いロープをつくります。短いロープを何本つくることができますか。
また、ロープは何mあまりますか。
筆算で出てきたあまりの “3” は、このままでいいのかな。
あまりがどうなるか確かめてみたいな。

小数で割る計算のあまりの大きさについて考えよう。
見通し
- あまりが3だと、割られる数より大きくなっておかしいな。(着眼の見通し)
- 図に表して考えよう。(方法の見通し)
- たしかめの計算をしてみよう。(方法の見通し)
- 割る数と割られる数をそれぞれ10倍、100倍して整数÷整数に直して考えてみると、あまりの大きさは割られる数の大きさに関係しているよ。(結果の見通し)
- あまりのある小数のわり算を筆算で解くと、あまりの小数点は割られる数の元の小数点と同じ場所になっているよ。(結果の見通し)
自力解決の様子
A つまずいている子
・あまりの意味と大きさについて理解できていないため、筆算で出てくる3をそのままあまりとしている。
5.1 ÷ 1.2 = 4あまり3 4本できて3mあまる。
B 素朴に解いている子
・テープ図などから、あまりの大きさを0.3としたほうが辻褄が合いそうだと思っている。
5.1 ÷ 1.2 = 4あまり0.3 4本できて0.3mあまる。
C ねらい通り解いている子
・「1.2×4+0.3=5.1」であることから、あまりが0.3であることの妥当性を確信している。
・「5.1÷1.2=4あまり0.3」について、「51÷12=4あまり3」「510÷120=4あまり30」などの計算の意味や筆算の仕方と比較して考え、あまりの大きさは割られる数の大きさに左右されることに目を向けている。
5.1 ÷ 1.2 = 4あまり0.3 4本できて0.3mあまる。
学び合いの計画
本時は、小数のわり算において初めてあまりが出る問題場面です。既習の整数のわり算の筆算ではあまりを修正することはなく、出た数をそのままあまりとして扱ってきた子供たちにとって難しく感じることが予想されます。
また、小数のわり算の筆算の過程で小数点を移動させて解くことを学んできた子供たちにとって、あまりの小数点は被除数の元の小数点にそろえるという方法に戸惑う子供の姿が予想されます。
そこで、小数のわり算におけるあまりの大きさについて確認します。例えば、テープ図や検算を用いてあまりが除数より小さくなること、この問題場面では小数になることを可視化すると理解しやすいです。
また、「除法の計算で、除数及び被除数に同じ数を掛けても商は変わらない」という性質を生かして、5.1÷1.2の計算は、(5.1×10)÷(1.2×10)= 51÷12 =4あまり3と考え、あまりは除数よりも小さくなることやあまりは被除数の大きさによって決まることを確認することもできます。
子供たちへの手立てとしてテープ図を用意し、必要な子供へ配付したり、デジタル教科書にあるテープ図を用いて大型提示装置で全体に示したりするなどが考えられます。
話合いでは、式と図、筆算をそれぞれつなげながら進めていきます。
前述の通り、戸惑うことが予想される場面なので、よく理解している子供だけで話合いを進めるのではなく、つまずいている子供も意図的指名や追体験などによって話合いに適時関わらせていくことで、小数のわり算におけるあまりの意味や筆算したときのあまりの小数点の位置についてより理解することができます。
ノート例
A つまずいている子
イラスト/横井智美

