小6算数「角柱と円柱の体積」 指導アイデア《円柱の体積の求め方》

執筆/中間市立中間西小学校教諭・河内一誠
監修/文部科学省教科調査官・笠井健一、福岡教育大学教授・清水紀宏

目次
単元計画
第1時 第5学年で学習した体積の学習をふり返り、体積の意味を確認する。
▼
第2時 図形の構成要素に着目し、直方体の体積を求める公式を捉え直し、四角柱の体積の求め方を考える。
▼
第3時 図形の構成要素に着目し、三角柱の体積の求め方を考える。
▼
第4時 (本時)図形の構成要素に着目し、円柱の体積の求め方を考える。
▼
第5時 図形の特徴に着目し、直方体を組み合わせた複合図形を角柱と見て、体積の求め方を考える。
▼
第6時 学習内容の習熟・定着を図る。
本時のねらい
図形の構成要素に着目し、円柱の体積の求め方を考え、説明する活動を通して、円柱の体積の公式を導き、円柱の体積を求めることができる。
評価規準
これまでの学習をふり返り、円柱の体積の公式を導こうとする。また、円柱の体積を求めることができる。(主体的に学習に取り組む態度、知識・技能)
本時の展開
※問題場面①を提示する。

三角柱の積み木の体積を求めましょう。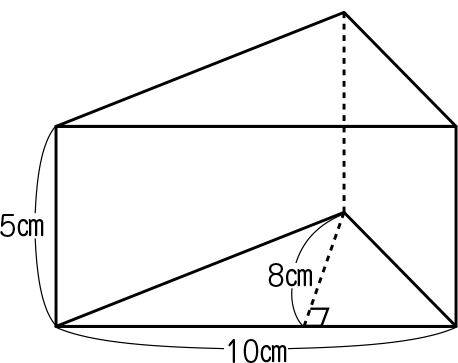
三角柱の積み木の体積を求めましょう。
角柱の体積の公式は、底面積×高さだったね。
10×8÷2×5=200で200㎤になります。
では、この積み木はどうですか。(問題場面②を提示する)

三角柱と円柱の積み木の体積は、どちらが大きいですか。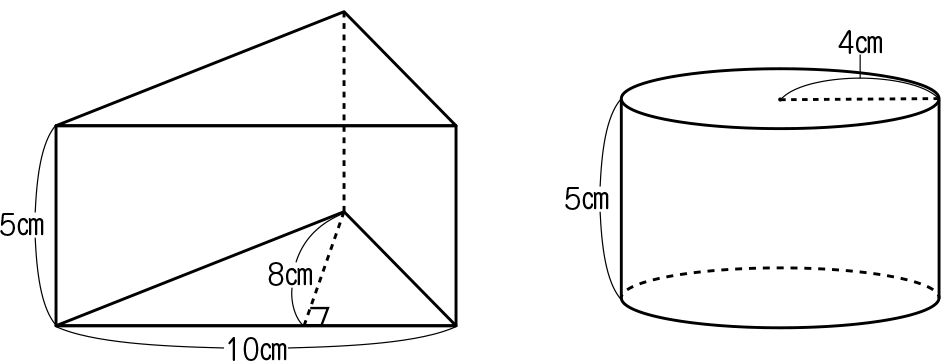
体積は同じくらいかな。
円柱の体積を求めればいいよ。
今日は円柱の体積の求め方を考えましょう。

円柱の体積の求め方を考えよう。
体積をどうやって求めていきましょうか。
角柱と同じように、底面積×高さで求めることができるんじゃないかな。
なるほど。でも、角柱と円柱は違う形だから、角柱の公式が使えるとは限りませんね。
角柱の学習と同じように、高さが1cmの円柱を求めて、それが積み重なっていると考えたらいいと思います。
※ICT機器などで直方体や三角柱の求積の学習をふり返る。
見通し
- 円柱の体積も(底面積)×(高さ)で求めることができる。
- 高さ1cmの円柱の体積を求め、積み重ねて考える。
導入では、前時の三角柱の体積の求積方法を確認します。
次に、本時で探究する円柱を三角柱と並べて出し、円柱の体積を求める動機付けとします。
前時までに角柱の体積が(底面積)×(高さ)であることを学習しているので、円柱の体積も(底面積)×(高さ)で求められるのではないか、と類推的に考えることは自然な発想でしょう。
本時では、「角柱と円柱は違う形だから、角柱の公式が使えるとは限りませんね」とゆさぶり発問をすることで、類推にとどまるのではなく、円柱の体積の求め方を考えていきます。
また、前時までの直方体、三角柱で求積公式をつくる学習をしているので、その学習をふり返って、本時の学習に生かそうとする態度を期待したいものです。
そうした態度が見受けられない場合は、前時までの学習をふり返ることを促していきましょう。
自力解決の様子
A つまずいている子
円の求積公式に誤りがあったり、忘れたりしているなど、円柱の体積を正しく求めることができない。
B 素朴に解いている子
・角柱の体積の公式を円柱に適用している。
4×4×3.14=50.24
50.24×5=251.2 251.2㎤
・高さ1cmの円柱の体積が底面の円の面積と同じであることを類推により予想し、円柱の求積方法を導いている。
C ねらい通り解いている子
・高さが1cmの円柱の体積を扇形に分割し、四角柱に変形することで、体積の数値と底面の円の面積の数値が同じことを確認し、円柱の求積方法を導いている。
・円柱を分割し、四角柱に変形し、円柱の体積が(底面積)×(高さ)であることを導いている。
学び合いの計画
Aの子供は円の面積を求めることができないので、個別に公式を確認し、見通しの通り、体積を計算するよう促します。
Bは円柱の体積が(底面積)×(高さ)であることを予想し、正しく答えを求めることができていますが、その根拠について考察していない状況です。
また、角柱の体積の公式を導く過程をふり返り、「高さが1cmの円柱の体積の数値と底面の面積の数値が同じ」と考える子供もいるでしょう。このことを根拠に円柱の体積の求め方を説明できれば、概ね満足な解法と言えます。
ただし、厳密には、それも予想に過ぎす、本当にそのことが正しいか確認する必要があります。
このことは、円の面積の求め方を使って確認されますが、個人解決で思い付くことは容易ではないので、全体の学び合いでICTなども使いながら確認してきましょう。
全体での学び合いでは、Bの考えを提示し、「4×4×3.14」と「×5」の意味を、見取り図と関連付けながら確認していきます。例えば、「このように積み重ねていく考え方を、どこかで使ったことがあるかな」と問いかけ、角柱の体積の学習で用いた求め方であることを想起させます。
その後、角柱の学習で高さ1㎝の角柱の体積の数値と底面の面積の数値が等しいことを確認しつつ、円柱でも同じことが成り立つか考えていきます。
ノート例
B 素朴に解いている子

C ねらい通りに解いている子

全体発表とそれぞれの考えの関連付け
円柱の体積は求められましたか。
イラスト/横井智美

