小3算数「あまりのあるわり算」指導アイデア《割る数よりあまりが小さくなる理由》

執筆/お茶の水女子大学附属小学校教諭・久下谷明
監修/文部科学省教科調査官・笠井健一、東京都目黒区立八雲小学校校長・長谷豊

目次
単元の展開
第1・2時(本時第2時) 割り切れない場合の計算の仕方(包含除) 14÷3
▼
第3時 割り切れない場合の計算の仕方(等分除) 16÷3
▼
第4時 割り切れない場合の除法の答えの確かめ方
▼
第5時 問題に応じた商の処理の仕方(あまりを考える問題)
▼
第6時 まとめ
本時のねらい
あまりと除数の関係に着目し、その関係を理解する。
評価規準
あまりが除数より小さくなることが分かり、そのわけを説明している。
本時の展開
下の問題を板書した後、まずは、次のようなやりとりを通して、あまりのあるわり算(割り切れる場合も含む)の計算の仕方を確認していきます。

あめが1●こあります。1人に 4こずつ分けると、何人に分けられて、何こあまりますか。あまりが出ない場合もあります。
●には0~9までの数字が入ります。例えば、もしも●が……。誰か、できそうな数字を1つ言ってくれますか。
それでは、3。
では、もしも、●が3だったら、そのときの問題はどのようになりますか。
「あめが13こあります。1人に 4こずつ分けると、何人に分けられて、何こあまりますか」となります。
式を立てて答えを求めることができそうですか。
あまりのあるわり算だね。
あまりが出そうですか。では、式を立てて答えを出しましょう。
※式を立てて、答えを求める。
式はどうなりますか。
13÷4です。
(短冊状に切った白画用紙に、ペンで式を書いて)答えはどうなりましたか。

13÷4=3あまり1。だから、3人に分けられて、1個あまります。
いいですね。答えの求め方を説明できる人はいますか。
4の段のかけ算で考え、4×3=12で、3人に分けることができて、でも、あめは13個あるから、13-12=1で1個あまります。
図で説明すると、このようになります。だから、3人に分けることができて、1個あまります。

そうですね。今説明してくれたように、あまりがあるときも、わり算の式で表して、これまでのわり算と同じように、割る数の段の九九を使って答えを見付けることができましたね。
※式に答えを書き加える。

※上記のように、あまりのあるわり算の式を最初に取り上げる際には、答えの求め方について、前時の学習を基にしながら、かけ算の式や図と関係付けて説明する時間をとり、確認するようにする。
では、ほかに●に0~9までの数字を入れると、どんな式ができそうですか。
5を入れて……。
●が5のとき、問題に対する式はどうなりますか。
15÷4です。
(短冊状に切った白画用紙にペンで式を書いて)では、答えはどうなりますか。

※計算をして答えを求める。
では、教えてください。
15÷4=3あまり3。だから、3人に分けられて、3個あまります。
※式に答えを書き加える。

では、ほかにどんな式ができそうですか。
6を入れて……、16÷4です。
割り切れそうですか。(短冊状に切った白画用紙にペンで式を書いて)答えはどうなりますか。

※計算をして答えを求める。
では、教えてください。
16÷4=4。だから4人に分けられます。
あまりは出ないね。
※式に答えを書き加える。
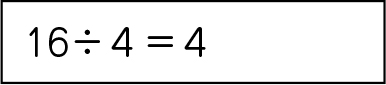
※上記のようなやりとりを、9回ほど繰り返した後、次のように問いかけて式を整理して並べるようにさせる。それをきっかけに、次の活動へと移っていく。
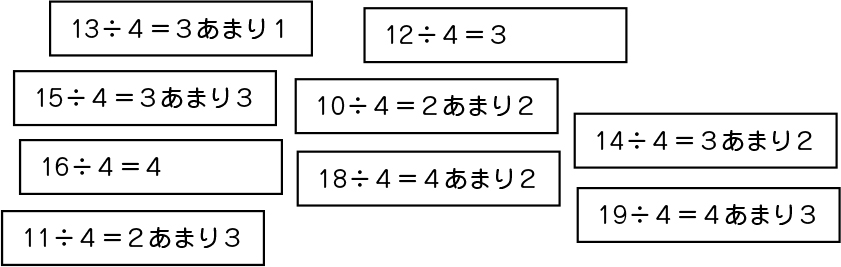
たくさんの式ができましたね。これで問題に対してすべての式ができましたか。
まだあります。
まだありますか。本当ですか。
あります!
すごいですね。式がばらばらに貼られていて、このままだとどの式がないのか分かりづらいので、見て、パッとこの式がないよというのが分かるように、式を整理して貼り直してくれますか。では、たくさんあるので、誰か2人、協力して貼り直してください。
※このような学習経験がない場合には、例えば「整理して1列に並べることができないかな?」、さらに「一番上には、どのわり算の式を置いたらいいかな?」と問いかけながら、並べていく際のきっかけを示すようにする。
※貼り直す。
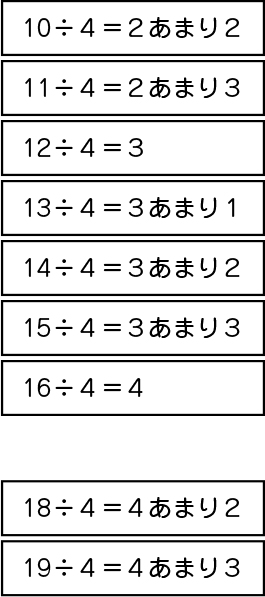
整理して貼り直してくれました。こうやって貼り直すと、まだ出ていない式があるのが分かりますか。
分かります。
それはどのような式ですか。
17÷4=4あまり1です。
その式は、どこに入りそうですか。
16÷4=4の下です。
そうですね。16÷4=4の下を空けてくれていますね。こうやってみると、確かに、17÷4=4あまり1がまだ出ていませんでしたね。(17÷4=4あまり1を白画用紙にペンで書いて加える。)これで、問題に合うすべての式が出ましたか。
はい。
先生、ちょっと気付いたことがあります。
えっ? ここに並んだ式を見て、何か気付くことがありますか。
あります。
まだありますか。本当ですか。
あります!
あります。あります。

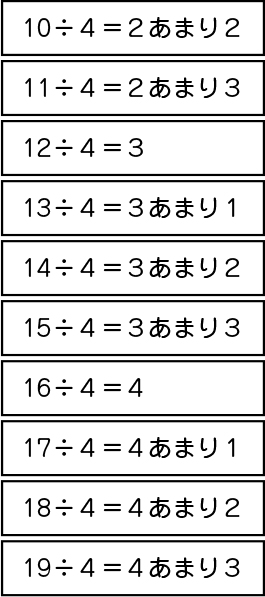
規則正しく並んだ式から、割る数とあまりの大きさについて考えよう。
今、ここにある規則正しく並んだ式を見て、気付いたことがあると言ってくれました。みなさんはどうですか。何か気付くことはありますか。少し時間を取るので、並んだ式を見て、気付くことはないか考えてみてください。(少し時間を取る)どうですか。何か気付いたことがある人はいますか。
※子供たちが挙手する。
考え中や悩み中の人はいますか。
※子供たちが挙手する。
考え中、悩み中の人もいますね。では、せっかくですので、同じ班の人とお話をする時間を取ります。何か気付いたことがある人は、同じ班の人にそれが伝わるように説明をしてください。また、悩み中、考え中の人も、友達の説明を聞きながら、気付いたことや思ったことがあったら、自分の考えを伝えてください。
※班で気付いたことを説明し、話し合う。
では、気付いたことを説明してください。
割られる数が10、11、12……と1ずつ増えています。
下から見ると1ずつ減っています。
答えが、2、3、4となっています。
※2が答えの式が2個、3が答えの式が4個、4が答えの式が4個のように、答えと式の個数に言及があった場合には、「8÷4=2」「9÷4=2あまり1」「7÷4=1あまり3」「20÷4=5」の式もやりとりを通して示しながら、同じ答えの式が4つずつあることを確認する。
見通し
あまりがなし、1、2、3と並んでいます。
確かに、あまりに注目すると、割り切れて、あまりがなし、1、2、3と並んでいますね。でもどうして、あまりは1、2、3なのでしょうか。割る数とあまりの大きさについて考え、ノートに説明をかきましょう。
どうしてあまりの数は、1、2、3?
自力解決の様子
A つまずいている子
あまりが1、2、3しかない(4や5などにはならない)ことは分かっているが、その理由を説明することができない。
B 素朴に解いている子
あまりが1、2、3しかないことは分かっていて、その説明として “あまりは割る数より必ず小さくなるから” といったことを書いている。
C ねらいどおり解いている子
あまりが1、2、3しかないことは分かっていて、その説明としてBの子の考えに加え、“もしもあまりが5だったら、まだ4で割ることができるから” といったことを図と関連付けながら説明を書いている。
学び合いの計画
並んだ式を見て、あまりが1、2、3しかないことは分かっていても、その理由をどのように説明してよいのか戸惑い、止まってしまう子がいます。
イラスト/横井智美

